60 Of 21
stanleys
Sep 14, 2025 · 6 min read
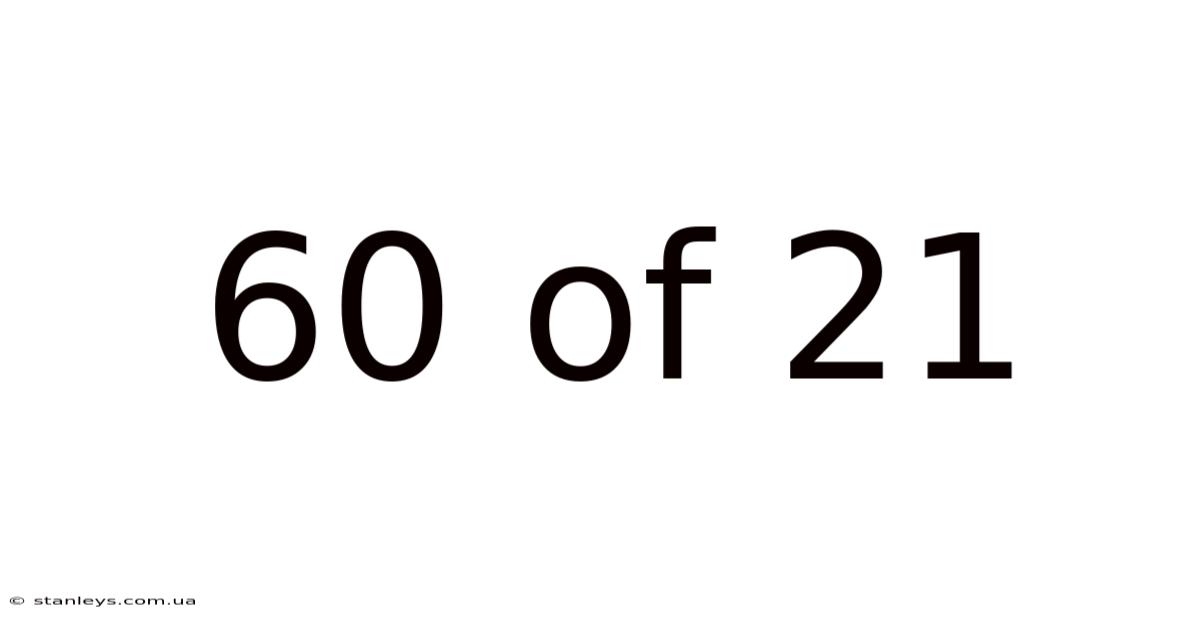
Table of Contents
Decoding the Enigma: A Deep Dive into 60/21 and its Mathematical Significance
The seemingly simple fraction 60/21 might appear unremarkable at first glance. However, a closer examination reveals a fascinating mathematical entity brimming with opportunities for exploration and understanding. This article delves into the intricacies of 60/21, exploring its simplification, decimal representation, applications in various mathematical contexts, and its relevance to broader mathematical concepts. We'll uncover its hidden beauty, demonstrating how even seemingly mundane numbers hold rich mathematical significance.
I. Introduction: Unveiling the Simplicity and Complexity of 60/21
The fraction 60/21, at its core, represents a ratio – the relationship between two quantities. While appearing straightforward, it presents a pathway to understanding fundamental mathematical processes such as simplification, conversion to decimals, and the application of ratios in real-world scenarios. This exploration will go beyond simple calculation, revealing the underlying principles and connections to broader mathematical concepts. Understanding 60/21 thoroughly allows for a deeper appreciation of fractional arithmetic and its place within the larger mathematical landscape.
II. Simplification: Finding the Essence of 60/21
The first step in analyzing 60/21 is simplification. This process involves finding the greatest common divisor (GCD) of the numerator (60) and the denominator (21) and dividing both by that GCD. Let's find the GCD of 60 and 21 using the Euclidean algorithm:
- 60 = 2 x 21 + 18
- 21 = 1 x 18 + 3
- 18 = 6 x 3 + 0
The last non-zero remainder is 3, indicating that the GCD of 60 and 21 is 3. Dividing both the numerator and the denominator by 3, we get:
60/3 = 20 21/3 = 7
Therefore, the simplified form of 60/21 is 20/7. This simplified fraction represents the same ratio but in its most concise form, making further calculations and interpretations easier. This process highlights the importance of simplification in making mathematical expressions more manageable and efficient.
III. Decimal Representation: Bridging the Gap Between Fractions and Decimals
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case, we divide 20 by 7:
20 ÷ 7 ≈ 2.85714285714...
The result is a repeating decimal, indicated by the repeating sequence "857142". This repeating pattern signifies that the decimal representation of 20/7 (and consequently 60/21) is not a terminating decimal (a decimal that ends). Understanding the difference between terminating and repeating decimals is crucial in various mathematical applications. The repeating decimal nature of 20/7 showcases the relationship between rational numbers (numbers that can be expressed as a fraction) and their decimal representations.
IV. Applications in Real-World Scenarios: Putting the Fraction to Work
The fraction 60/21, or its simplified form 20/7, can be applied in various real-world situations. Imagine a scenario involving ratios and proportions:
-
Recipe Scaling: A recipe calls for 21 grams of flour and 60 grams of sugar. To scale the recipe up or down, the ratio 60/21 (or 20/7) remains constant. Multiplying both the numerator and the denominator by the same scaling factor maintains the correct proportions.
-
Speed and Distance: A car travels 60 kilometers in 21 minutes. The ratio 60/21 represents the speed in kilometers per minute. Simplifying to 20/7 provides a clearer representation of the speed.
-
Unit Conversion: Consider a situation where you need to convert units. The ratio could represent a conversion factor between two different units of measurement, needing to be simplified for easier calculation.
These examples illustrate that the seemingly abstract concept of a fraction finds practical applications in various real-world contexts, emphasizing the importance of understanding fractional arithmetic.
V. Mathematical Connections: Expanding the Horizon
The fraction 60/21 provides an excellent opportunity to explore deeper mathematical concepts:
-
Rational Numbers: Both 60/21 and its simplified form 20/7 are rational numbers, meaning they can be expressed as a fraction of two integers. This is a fundamental concept in number theory.
-
Ratio and Proportion: The fraction embodies the concept of ratio and proportion, fundamental to algebra and geometry. Understanding ratios helps in solving problems involving scaling, similarity, and proportions.
-
Decimal Expansion and Continued Fractions: The repeating decimal expansion of 20/7 can be further analyzed using the concept of continued fractions, providing a different perspective on representing rational numbers.
-
Modular Arithmetic: The numerator and denominator can be used in exploring concepts in modular arithmetic, where numbers "wrap around" after reaching a certain value.
VI. Advanced Applications: Exploring Further
Beyond the basic applications, 60/21 can be utilized in more advanced mathematical contexts:
-
Calculus: In calculus, understanding the behavior of rational functions (functions expressed as ratios of polynomials) is crucial. Analyzing the limits and derivatives of functions related to 60/21 can provide valuable insights.
-
Linear Algebra: Matrices and vectors often involve ratios and proportions, and the principles learned from understanding 60/21 are transferable to linear algebra problems.
-
Number Theory: Exploring the prime factorization of 60 (2² x 3 x 5) and 21 (3 x 7) can lead to deeper investigations in number theory, particularly related to divisibility and prime numbers.
VII. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 60/21?
- A: The simplest form of 60/21 is 20/7.
-
Q: Is 60/21 a rational number?
- A: Yes, 60/21 is a rational number because it can be expressed as a fraction of two integers.
-
Q: What is the decimal representation of 60/21?
- A: The decimal representation of 60/21 is approximately 2.85714285714..., a repeating decimal.
-
Q: How can I use 60/21 in real-world problems?
- A: 60/21 can be used to represent ratios and proportions in various scenarios such as recipe scaling, speed and distance calculations, and unit conversions.
-
Q: Are there any advanced mathematical concepts related to 60/21?
- A: Yes, concepts such as continued fractions, rational functions, and number theory can be explored in relation to 60/21.
VIII. Conclusion: The Profound Simplicity of a Single Fraction
While appearing initially simple, the fraction 60/21 serves as a powerful tool to illustrate fundamental and advanced mathematical concepts. Through simplification, decimal conversion, real-world application, and exploration of its mathematical connections, we've uncovered the rich tapestry of mathematical ideas interwoven within this seemingly unremarkable fraction. This exploration highlights the interconnectedness of mathematical concepts and the importance of understanding even seemingly basic mathematical operations. The journey from 60/21 to 20/7, and beyond, reveals the beauty and depth hidden within the seemingly simple world of numbers. Understanding this simple fraction unlocks a deeper appreciation for the elegance and power of mathematics. The next time you encounter a seemingly simple fraction, remember the intricate beauty and vast potential for exploration it holds.
Latest Posts
Latest Posts
-
Information Data Difference
Sep 14, 2025
-
3c To Fahrenheit
Sep 14, 2025
-
Kj In Kw
Sep 14, 2025
-
7 5 In Centimeters
Sep 14, 2025
-
112 4kg In Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.