60 Of 180
stanleys
Sep 13, 2025 · 5 min read
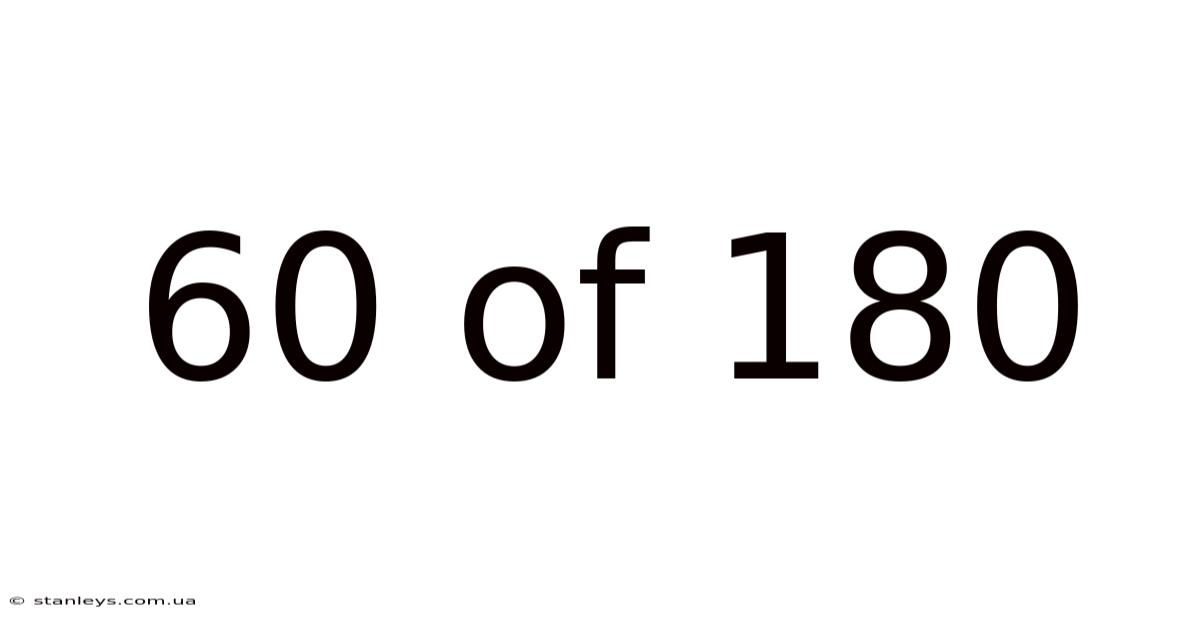
Table of Contents
Decoding the Fraction: Understanding 60/180 and its Implications
The seemingly simple fraction 60/180 might appear straightforward at first glance. However, understanding this fraction goes beyond basic arithmetic; it delves into the core principles of fractions, ratios, percentages, and their practical applications in various fields. This comprehensive guide will explore 60/180 in depth, offering explanations suitable for learners of all levels, from elementary school students to those seeking a refresher on fundamental mathematical concepts. We'll move beyond simple simplification to explore the broader context and implications of this fraction.
Understanding Fractions: A Quick Refresher
Before diving into 60/180, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number (60 in this case) indicates the number of parts we're considering.
- Denominator: The bottom number (180 in this case) indicates the total number of equal parts that make up the whole.
Therefore, 60/180 means we are considering 60 out of a total of 180 equal parts.
Simplifying 60/180: Finding the Lowest Terms
The first step in working with fractions is often to simplify them to their lowest terms. This means reducing the fraction to its simplest form, where the numerator and denominator share no common factors other than 1. This process involves finding the greatest common divisor (GCD) of the numerator and denominator.
To find the GCD of 60 and 180, we can use several methods, including prime factorization or the Euclidean algorithm. Let's use prime factorization:
- Prime factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
- Prime factorization of 180: 2 x 2 x 3 x 3 x 5 = 2² x 3² x 5
The common factors are 2², 3, and 5. Multiplying these together gives us 60 (2² x 3 x 5 = 60). Dividing both the numerator and denominator by 60, we get:
60 ÷ 60 / 180 ÷ 60 = 1/3
Therefore, the simplified form of 60/180 is 1/3. This means that 60 is one-third of 180.
Visualizing 60/180: A Pictorial Representation
Visualizing fractions can make them easier to understand. Imagine a circle divided into 180 equal slices. If you take 60 of these slices, you've taken one-third of the entire circle. This visual representation reinforces the concept that 60/180 is equivalent to 1/3. You can apply this visualization to other shapes and scenarios to build a stronger intuition for fractions.
Converting 60/180 to a Percentage
Fractions can be easily converted to percentages, offering another way to represent the same value. To convert a fraction to a percentage, we multiply the fraction by 100%.
(60/180) x 100% = (1/3) x 100% ≈ 33.33%
Therefore, 60/180 represents approximately 33.33%. This indicates that 60 is approximately 33.33% of 180.
Real-World Applications of 60/180 (or 1/3)
The fraction 1/3 (and its equivalent 60/180) appears frequently in various real-world contexts:
- Cooking and Baking: Recipes often use ratios of ingredients. A recipe might call for 1/3 cup of sugar, which is easily understood and measurable.
- Construction and Engineering: Measurements and proportions in building projects frequently involve fractions, ensuring accuracy and scale. A blueprint might specify a length as 1/3 of a total dimension.
- Finance: Dividing assets, calculating proportions of investments, and understanding profit margins often involve fractions.
- Data Analysis: Representing portions of a dataset or expressing probabilities frequently requires using fractions or their percentage equivalents.
- Science: Many scientific calculations and ratios utilize fractions to accurately represent measurements and relationships between variables.
Understanding 1/3 allows for accurate calculations and informed decision-making in these and many other scenarios.
Understanding Ratios: The Relationship between 60 and 180
The fraction 60/180 can also be interpreted as a ratio. A ratio expresses the relationship between two quantities. In this case, the ratio of 60 to 180 is 60:180, which simplifies to 1:3. This means that for every one part of 60, there are three parts of 180. This ratio is fundamental in understanding proportional relationships.
Beyond Simplification: Exploring Deeper Mathematical Concepts
While simplifying the fraction to 1/3 is crucial, understanding 60/180 also opens doors to exploring more advanced mathematical concepts:
- Proportions: Setting up and solving proportions using this fraction allows for solving real-world problems where quantities are proportionally related.
- Algebra: Representing unknown quantities using variables and solving equations involving fractions like 60/180 strengthens algebraic skills.
- Geometry: Fractions are essential in calculating areas, volumes, and other geometrical properties. The ratio 1:3 can represent the relationship between the sides of similar triangles, for instance.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 60/180?
A: The simplest form of 60/180 is 1/3.
Q: How do I convert 60/180 to a decimal?
A: Divide the numerator (60) by the denominator (180). 60 ÷ 180 = 0.333... (a repeating decimal).
Q: What is the percentage equivalent of 60/180?
A: The percentage equivalent of 60/180 is approximately 33.33%.
Q: Can 60/180 be expressed as a mixed number?
A: No, since the numerator (60) is smaller than the denominator (180), it cannot be expressed as a mixed number. A mixed number is a combination of a whole number and a proper fraction.
Q: What are some real-world examples where this fraction is used?
A: Numerous real-world examples exist, including cooking, construction, finance, and data analysis, as described above.
Conclusion: The Significance of Mastering Fractions
Understanding the fraction 60/180, and its simplified form 1/3, is not just about basic arithmetic; it's about grasping fundamental mathematical principles with far-reaching implications. From simplifying fractions and converting to percentages to understanding ratios and applying these concepts to real-world problems, mastering fractions like 60/180 builds a strong foundation for success in various academic and professional fields. The seemingly simple act of reducing a fraction unlocks a world of mathematical understanding and problem-solving capabilities. Continuously practicing and applying these concepts will strengthen your mathematical intuition and make you a more confident and capable problem solver. Don't underestimate the power of understanding fractions; they are the building blocks of many advanced mathematical concepts.
Latest Posts
Latest Posts
-
8lbs 4oz Kilograms
Sep 13, 2025
-
159lbs To Kg
Sep 13, 2025
-
Is Sulfur Diatomic
Sep 13, 2025
-
78inches To Feet
Sep 13, 2025
-
8 7kg In Pounds
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.