60 Of 18
stanleys
Sep 12, 2025 · 6 min read
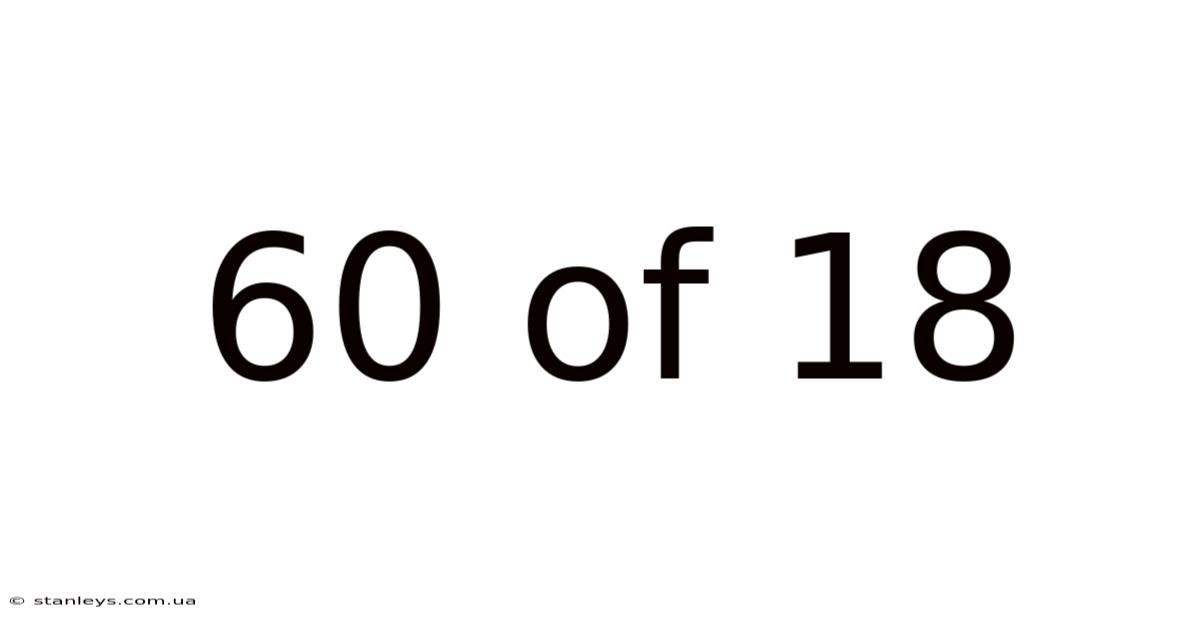
Table of Contents
Understanding the Fraction 60/18: Simplification, Decimals, and Applications
The fraction 60/18, while seemingly simple at first glance, offers a rich opportunity to explore fundamental concepts in mathematics. This article delves into the simplification of this fraction, its decimal equivalent, practical applications, and answers frequently asked questions about working with such fractions. Understanding fractions like 60/18 is crucial for building a solid foundation in arithmetic, algebra, and beyond.
I. Introduction: Simplifying 60/18
The fraction 60/18 represents 60 parts out of a total of 18 parts. This immediately suggests that the fraction is improper, meaning the numerator (60) is larger than the denominator (18). Improper fractions are perfectly valid, but they are often simplified to make them easier to understand and work with. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
The GCD of 60 and 18 is 6. We can find this through prime factorization:
- 60 = 2 x 2 x 3 x 5
- 18 = 2 x 3 x 3
The common factors are 2 and 3. Therefore, the GCD is 2 x 3 = 6.
Dividing both the numerator and the denominator by 6, we get:
60 ÷ 6 = 10 18 ÷ 6 = 3
Therefore, the simplified form of 60/18 is 10/3. This is still an improper fraction, representing more than one whole unit.
II. Converting to Mixed Number and Decimal
Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction. To convert 10/3 to a mixed number, we perform division:
10 ÷ 3 = 3 with a remainder of 1.
This means 10/3 is equal to 3 1/3. This representation shows that 10/3 is equivalent to three whole units and one-third of another unit.
To convert 10/3 to a decimal, we simply divide 10 by 3:
10 ÷ 3 ≈ 3.333...
The decimal representation is a repeating decimal, indicated by the ellipsis (...). The digit 3 repeats infinitely. We can round this to a certain number of decimal places depending on the required precision, for example, 3.33 or 3.3333.
III. Practical Applications of 60/18 and its Equivalents
Fractions like 60/18 and its simplified form, 10/3, appear frequently in various real-world scenarios. Consider these examples:
-
Baking: A recipe calls for 60 grams of flour and 18 grams of sugar. The ratio of flour to sugar is 60/18, which simplifies to 10/3. This means for every 3 grams of sugar, you need 10 grams of flour.
-
Construction: A project requires 60 feet of lumber and the available length is 18 feet per piece. The calculation 60/18 determines how many pieces of lumber are needed (3 and 1/3 pieces, meaning 4 pieces are required to ensure sufficient lumber).
-
Geometry: Imagine a rectangle with an area of 60 square units and a width of 18 units. The length of the rectangle is found by dividing the area by the width: 60/18 = 10/3 units.
-
Data Analysis: If a survey shows 60 respondents out of 180 total prefer a particular product, the fraction 60/180 simplifies to 1/3, representing the proportion of respondents favoring that product.
These examples highlight the versatility of fractions in solving practical problems across diverse fields. Understanding how to simplify, convert, and interpret fractions is essential for accurate calculations and insightful analysis.
IV. Working with Fractions: Addition, Subtraction, Multiplication, and Division
While simplifying 60/18 is a crucial first step, we often need to perform further operations with fractions. Here's a brief overview of the basic operations:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. For example, adding 10/3 and 2/3 is straightforward: (10 + 2)/3 = 12/3 = 4. If the denominators are different, we must find a least common multiple (LCM) and adjust the fractions accordingly.
-
Multiplication: Multiplying fractions is simpler. We multiply the numerators together and the denominators together: (10/3) x (2/5) = (10 x 2) / (3 x 5) = 20/15 = 4/3.
-
Division: To divide fractions, we invert the second fraction (the divisor) and then multiply: (10/3) ÷ (2/5) = (10/3) x (5/2) = 50/6 = 25/3.
Mastering these operations is crucial for effectively using fractions in problem-solving.
V. Further Exploration: Ratios and Proportions
The fraction 60/18 can also be interpreted as a ratio: 60 to 18. Ratios compare two quantities. This ratio can be simplified to 10:3, meaning the relationship between the two quantities is 10 to 3. This concept is fundamental in understanding proportions, which are statements of equality between two ratios. Proportions are used extensively in scaling, mapping, and other applications.
For instance, if we know that the ratio of flour to sugar in a recipe is 10:3, and we want to make a larger batch using 30 grams of sugar, we can set up a proportion to find the required amount of flour:
10/3 = x/30
Solving for x, we find x = 100 grams of flour.
VI. Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 60/18?
A1: The simplest form of 60/18 is 10/3.
Q2: Is 60/18 a proper or improper fraction?
A2: 60/18 is an improper fraction because the numerator (60) is greater than the denominator (18).
Q3: How do I convert 60/18 to a decimal?
A3: First, simplify 60/18 to 10/3. Then, divide 10 by 3 to get approximately 3.333...
Q4: What are some real-world applications of 60/18?
A4: 60/18 (or 10/3) can be applied in various scenarios such as recipe scaling, construction measurements, geometrical calculations, and data analysis as explained above.
Q5: How do I add or subtract fractions with different denominators?
A5: Find the least common multiple (LCM) of the denominators. Convert each fraction to an equivalent fraction with the LCM as the denominator, and then add or subtract the numerators.
VII. Conclusion: The Significance of Fractional Understanding
The seemingly simple fraction 60/18 provides a gateway to a deeper understanding of fundamental mathematical concepts. Through simplification, conversion to mixed numbers and decimals, practical application examples, and the exploration of ratios and proportions, this article has demonstrated the importance of mastering fraction manipulation. This knowledge is not just for academic success but is a cornerstone for problem-solving and critical thinking in various aspects of life. By understanding and practicing these concepts, you build a robust mathematical foundation that will serve you well in future studies and endeavors. The ability to confidently work with fractions empowers you to tackle complex problems with clarity and precision.
Latest Posts
Latest Posts
-
32km In Miles
Sep 12, 2025
-
Victorian Era Cosmetics
Sep 12, 2025
-
Anti Bumping Granules
Sep 12, 2025
-
Cool Runnings Quotes
Sep 12, 2025
-
How Your Today
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.