60 Of 130
stanleys
Sep 17, 2025 · 6 min read
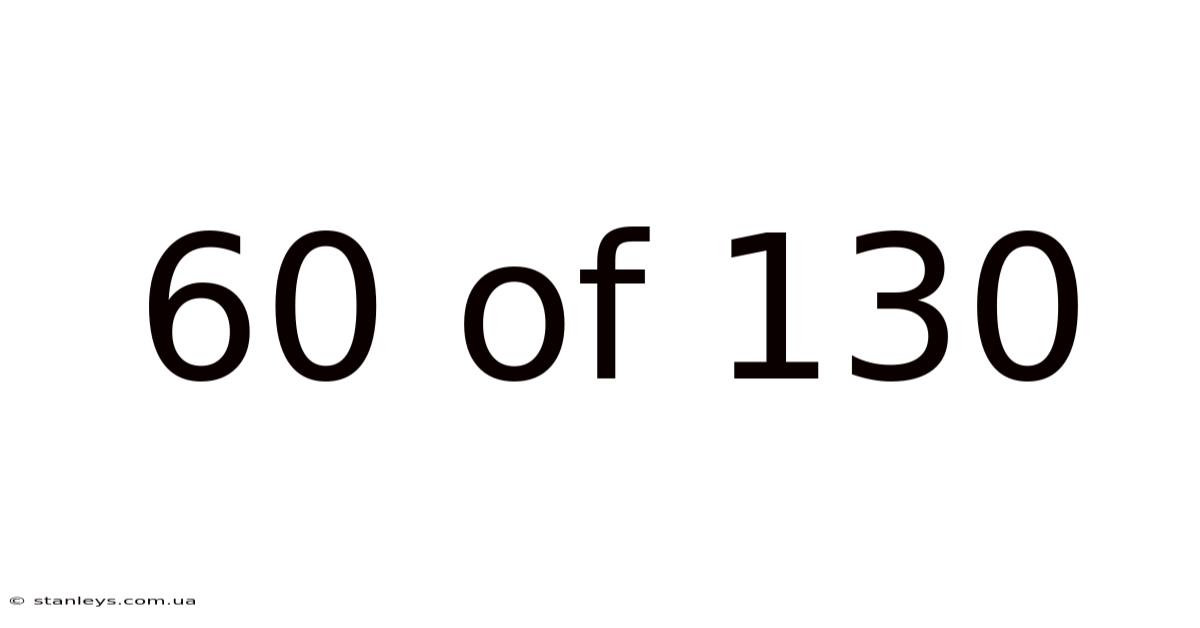
Table of Contents
Decoding the Fraction: Understanding 60/130 and its Implications
The seemingly simple fraction 60/130 might appear insignificant at first glance. However, understanding this fraction—its simplification, its decimal equivalent, its percentage representation, and its broader mathematical implications—opens doors to a deeper understanding of fundamental mathematical concepts. This article will explore 60/130 in detail, providing clear explanations and practical examples suitable for learners of all levels. We'll delve into the process of simplification, conversion to decimals and percentages, and discuss real-world applications to solidify your understanding.
Introduction: The Basics of Fractions
Before diving into the specifics of 60/130, let's briefly revisit the core concept of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number, indicating the number of parts you have) and the denominator (the bottom number, indicating the total number of parts). In the fraction 60/130, 60 is the numerator and 130 is the denominator. This means we have 60 parts out of a possible 130 parts.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms. This is done by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both numbers without leaving a remainder.
Let's find the GCD of 60 and 130. We can use the Euclidean algorithm or list the factors of each number to find the GCD.
- Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Factors of 130: 1, 2, 5, 10, 13, 26, 65, 130
By comparing the lists, we see that the greatest common factor is 10.
Now, we divide both the numerator and the denominator by 10:
60 ÷ 10 = 6 130 ÷ 10 = 13
Therefore, the simplified form of 60/130 is 6/13. This simplified fraction is equivalent to the original fraction, but it's expressed in a more concise and manageable form.
Converting to Decimal: From Fraction to Decimal Representation
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we divide 6 by 13:
6 ÷ 13 ≈ 0.4615
The result is an approximate decimal value because the division results in a repeating decimal. The exact decimal representation of 6/13 is 0.461538461538... The digits "461538" repeat infinitely. For practical purposes, we often round the decimal to a specific number of decimal places, such as 0.46.
Converting to Percentage: Expressing the Fraction as a Percentage
A percentage is a fraction expressed as a part of 100. To convert a fraction to a percentage, we first convert it to a decimal and then multiply by 100%.
Using the decimal approximation 0.4615 from above:
0.4615 × 100% ≈ 46.15%
Therefore, 60/130 is approximately 46.15%. This percentage representation provides a readily understandable way to express the proportional relationship between 60 and 130.
Real-World Applications of 60/130 and Similar Fractions
Understanding fractions like 60/130 is crucial in various real-world situations. Here are some examples:
-
Calculating proportions: Imagine you have 130 apples, and 60 of them are red. The fraction 60/130 (or its simplified form 6/13) represents the proportion of red apples. This is useful for analyzing data, making predictions, or comparing different quantities.
-
Determining percentages in surveys or polls: Suppose a survey of 130 people shows that 60 prefer a particular brand. The fraction 60/130, converted to a percentage (approximately 46.15%), gives the percentage of people who prefer that brand.
-
Solving problems involving ratios: Ratios are similar to fractions and often used to compare quantities. If a recipe calls for a ratio of 6 parts sugar to 13 parts flour, you can express this ratio as 6/13, which is equivalent to 60/130.
-
Calculating discounts: If an item is discounted by 60/130 of its original price, you can simplify the fraction to 6/13 and then calculate the discount percentage.
-
Understanding probabilities: In probability calculations, fractions represent the likelihood of an event occurring. For instance, if there is a 60/130 chance of a specific outcome, simplifying and converting to a percentage provides a clear understanding of the probability.
Mathematical Implications and Further Exploration
The fraction 60/130, and its simplified form 6/13, can be used to explore various mathematical concepts:
-
Equivalent fractions: Many fractions are equivalent to 6/13, including 12/26, 18/39, 24/52, and so on. These fractions all represent the same proportional value.
-
Rational numbers: Fractions like 6/13 are examples of rational numbers, which can be expressed as a ratio of two integers.
-
Decimal expansions: The decimal expansion of 6/13 reveals the concept of repeating decimals. Understanding why some fractions have terminating decimals and others have repeating decimals is a key concept in number theory.
-
Approximations: Since the decimal representation of 6/13 is a repeating decimal, approximations are often used in practical calculations. The level of accuracy required determines the number of decimal places to retain.
-
Proportionality: The relationship between the numerator and denominator in 6/13 illustrates the concept of proportionality. Changes in the numerator and denominator maintain the same ratio, which is a fundamental concept in many areas of mathematics and science.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to work with, understand, and compare. It reduces complexity and provides a more concise representation of the proportional relationship.
-
Q: How do I know if a fraction is in its simplest form?
- A: A fraction is in its simplest form when the greatest common divisor of the numerator and denominator is 1. This means there are no common factors other than 1.
-
Q: Can I use a calculator to simplify fractions?
- A: Many calculators have functions to simplify fractions. Alternatively, you can use online fraction calculators. However, understanding the manual process of finding the GCD is essential for building a strong mathematical foundation.
-
Q: What if the decimal representation of a fraction doesn't terminate?
- A: Many fractions have non-terminating, repeating decimal representations. This is perfectly acceptable, and these numbers are still perfectly valid rational numbers. We can use approximations when dealing with them in practical calculations.
-
Q: Are there any other methods to find the GCD besides listing factors?
- A: Yes, the Euclidean algorithm is a more efficient method, especially for larger numbers. This algorithm involves a series of divisions until the remainder is zero. The last non-zero remainder is the GCD.
Conclusion: Mastering Fractions – A Building Block for Further Learning
Understanding fractions, even seemingly simple ones like 60/130, is crucial for building a strong foundation in mathematics. The process of simplifying, converting to decimals and percentages, and understanding the real-world applications of these concepts are essential skills applicable to various disciplines. This comprehensive exploration of 60/130 not only elucidates its numerical properties but also highlights the broader significance of fractions in mathematics and beyond. By mastering these fundamental concepts, you are well-equipped to tackle more complex mathematical problems and confidently apply these skills in various real-world scenarios. Remember that the journey of learning is continuous, and each concept mastered opens up new avenues for further exploration and discovery.
Latest Posts
Latest Posts
-
Merry Cone Spanish
Sep 17, 2025
-
9 Times 4
Sep 17, 2025
-
235 Kph Mph
Sep 17, 2025
-
Calcium Hydrochloric Acid
Sep 17, 2025
-
21km In Miles
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 130 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.