56 Of 850
stanleys
Sep 14, 2025 · 5 min read
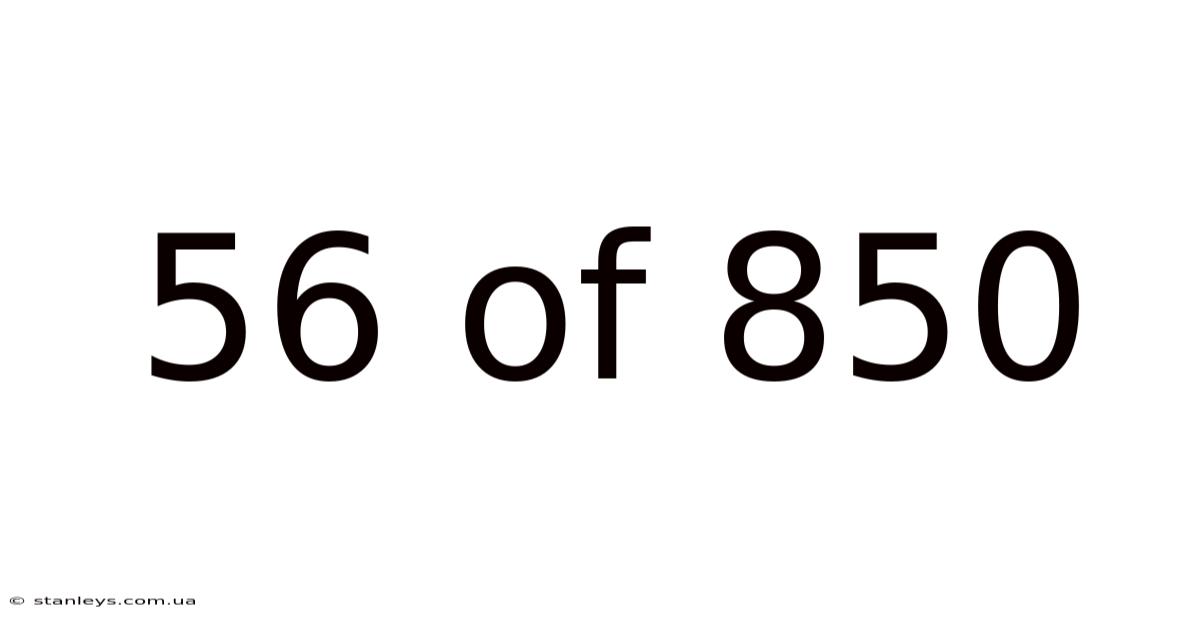
Table of Contents
Decoding the Fraction: Understanding 56 out of 850
The seemingly simple fraction 56/850 often presents itself in various contexts, from academic assessments to data analysis in the workplace. Understanding this fraction goes beyond simply stating its numerical value; it involves grasping its implications, representing it effectively, and using it in problem-solving. This article will delve deep into the meaning and applications of 56 out of 850, exploring its representation as a percentage, decimal, and its significance within larger datasets. We’ll also look at how to simplify the fraction and address common misconceptions.
Understanding the Basics: What Does 56 out of 850 Mean?
The fraction 56/850 represents a part-to-whole relationship. It tells us that 56 is a portion of a larger total of 850. Imagine, for example, 850 students took an exam, and 56 of them achieved a perfect score. In this case, 56/850 signifies the proportion of students who achieved a perfect score. This fraction can be applied to countless scenarios involving proportions, percentages, and ratios.
Converting the Fraction: Percentage Representation
One of the most common ways to interpret a fraction is by expressing it as a percentage. To convert 56/850 into a percentage, we perform the following calculation:
(56 / 850) * 100%
This calculation yields approximately 6.59%. This means that 56 represents approximately 6.59% of the total 850. This percentage representation offers a more intuitive understanding of the fraction's magnitude, making it easier to compare with other proportions. For instance, if another group achieved a 10% success rate, we can immediately see that the 6.59% success rate of 56 out of 850 is lower.
Converting the Fraction: Decimal Representation
Another useful representation is the decimal equivalent. To obtain this, we simply divide 56 by 850:
56 / 850 ≈ 0.0659
The decimal 0.0659 provides a precise numerical representation of the fraction, facilitating mathematical operations and comparisons. This decimal form is particularly useful in spreadsheet software or programming, where calculations are performed directly on numerical values.
Simplifying the Fraction: Finding the Lowest Terms
While 56/850 is a perfectly valid representation, it can be simplified to a smaller, equivalent fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator (56) and the denominator (850) by their greatest common divisor (GCD).
The GCD of 56 and 850 is 2. Dividing both numbers by 2, we get:
56 / 2 = 28 850 / 2 = 425
Therefore, the simplified fraction is 28/425. This simplified fraction represents the same proportion as 56/850 but is more concise and easier to work with in certain calculations.
Applications of 56/850 in Real-World Scenarios
The fraction 56/850, and its simplified form 28/425, can be applied in diverse fields:
-
Statistics and Data Analysis: Imagine analyzing survey results where 56 out of 850 respondents answered "yes" to a particular question. The fraction provides the proportion of "yes" responses, crucial for drawing statistical conclusions.
-
Quality Control: In manufacturing, if 56 out of 850 products fail quality control, the fraction highlights the defect rate. This information informs decision-making regarding production processes and quality improvement strategies.
-
Academic Performance: If 56 out of 850 students passed an exam, the fraction represents the pass rate, allowing educators to assess the effectiveness of teaching methods and curriculum.
-
Financial Analysis: In investment, 56/850 could represent the proportion of successful investments out of a total portfolio. This information contributes to risk assessment and portfolio optimization.
-
Scientific Research: In experimental studies, 56/850 might represent the number of positive outcomes out of the total number of trials. This data is essential for drawing conclusions about the effectiveness of a treatment or methodology.
Expanding the Understanding: Ratios and Proportions
The fraction 56/850 can also be expressed as a ratio: 56:850 (read as "56 to 850"). Ratios are used to compare the relative sizes of two or more quantities. In this context, the ratio indicates that for every 850 units of the whole, there are 56 units of the specific part.
Understanding proportions involves finding equivalent ratios. For example, 56/850 is equivalent to 28/425, 14/212.5, and many other ratios. The concept of proportion is crucial in solving problems involving scaling and similar figures.
Addressing Common Misconceptions
A common misconception is confusing the fraction with a percentage without performing the necessary conversion. Remember, the fraction itself does not directly represent a percentage; the percentage is derived from the fraction through calculation.
Another misconception is neglecting to simplify fractions. While a fraction like 56/850 is perfectly valid, simplifying it to 28/425 makes calculations and comparisons easier and promotes clearer communication.
Further Exploration: Working with Larger Datasets
While this article focuses on 56/850, the principles discussed extend to larger datasets. The same methods – conversion to percentage and decimal, simplification, and understanding the part-to-whole relationship – remain applicable when dealing with larger numbers. Tools like spreadsheets and statistical software greatly assist in managing and analyzing such datasets.
Conclusion: The Significance of Understanding Fractions
The seemingly simple fraction 56/850 holds significant value in numerous contexts. Understanding its representation as a percentage and decimal, its simplified form, and its broader implications within ratios and proportions are essential skills for anyone dealing with data analysis, statistical interpretation, or problem-solving involving proportions. By mastering the principles discussed, you gain a powerful tool for navigating a wide range of quantitative situations. Remember that accurately interpreting and manipulating fractions is a fundamental skill applicable across various disciplines. Continuous practice and exposure to real-world applications are key to solidifying this understanding.
Latest Posts
Latest Posts
-
Burgundy Coat Dog
Sep 14, 2025
-
17cms In Inches
Sep 14, 2025
-
35pounds To Kg
Sep 14, 2025
-
70 Of 65
Sep 14, 2025
-
Lee Friedlander Photographer
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 56 Of 850 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.