54 Of 216
stanleys
Sep 17, 2025 · 6 min read
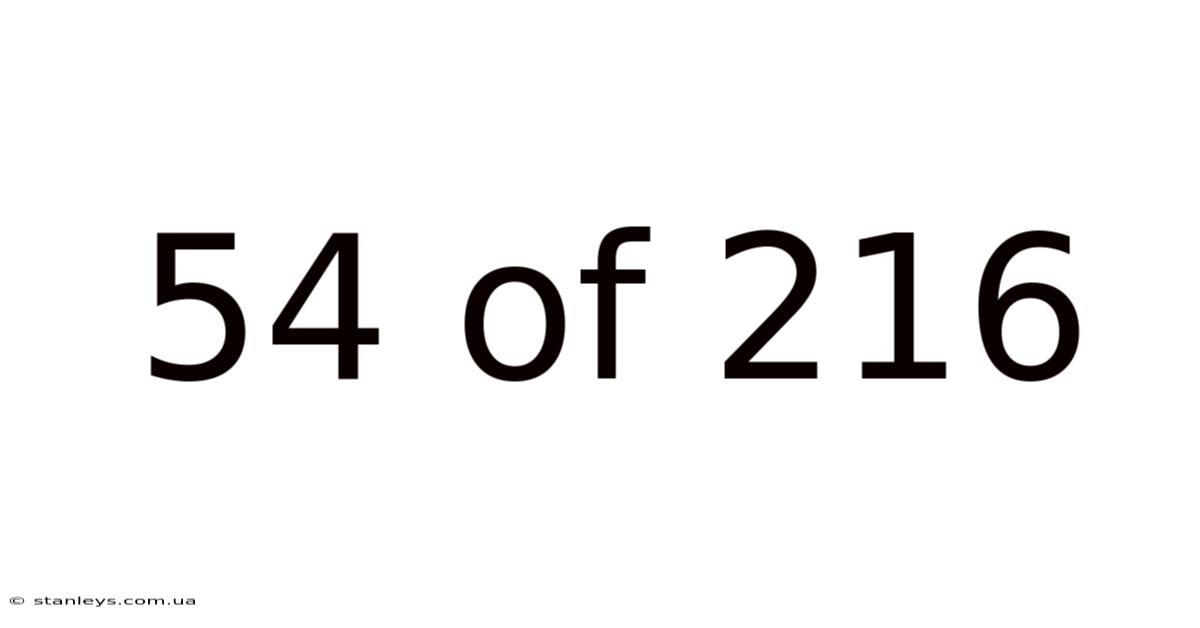
Table of Contents
Decoding the Fraction 54/216: A Deep Dive into Simplification and its Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article delves into the fraction 54/216, exploring its simplification, underlying mathematical principles, and practical examples demonstrating its relevance. We'll uncover how to reduce this fraction to its simplest form, explore the concept of equivalent fractions, and examine real-world scenarios where such calculations are essential. By the end, you'll have a comprehensive understanding of 54/216 and its significance.
Introduction: Understanding the Basics of Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In the fraction 54/216, 54 is the numerator and 216 is the denominator. This means we have 54 parts out of a possible 216 equal parts.
Simplifying 54/216: Finding the Greatest Common Divisor (GCD)
The key to understanding 54/216 lies in simplifying it. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This process involves finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers without leaving a remainder.
Several methods exist for finding the GCD:
-
Listing Factors: List all the factors of 54 and 216, then identify the largest factor they share. This method can be time-consuming for larger numbers. Factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54. Factors of 216 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216. The largest common factor is 54.
-
Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
54 = 2 x 3 x 3 x 3 = 2 x 3³ 216 = 2 x 2 x 2 x 3 x 3 x 3 = 2³ x 3³
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ (or 2) and the lowest power of 3 is 3³. Therefore, the GCD is 2 x 3³ = 2 x 27 = 54.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
216 ÷ 54 = 4 with a remainder of 0.
Since the remainder is 0, the GCD is 54.
Now that we've found the GCD (54), we can simplify the fraction:
54/216 = (54 ÷ 54) / (216 ÷ 54) = 1/4
Therefore, the simplest form of 54/216 is 1/4.
Equivalent Fractions: Exploring Different Representations
It's crucial to understand that 54/216 and 1/4 are equivalent fractions. They represent the same proportion or value. Any fraction can be expressed in multiple equivalent forms by multiplying or dividing both the numerator and denominator by the same non-zero number. For example:
- 2/8 is equivalent to 1/4 (divide both by 2)
- 3/12 is equivalent to 1/4 (divide both by 3)
- 108/432 is equivalent to 1/4 (divide both by 108)
Real-World Applications of Fraction Simplification
Simplifying fractions isn't just a mathematical exercise; it has practical applications in various fields:
-
Cooking and Baking: Recipes often require precise measurements. Simplifying fractions helps in scaling recipes up or down accurately. If a recipe calls for 54g of flour out of a total of 216g of ingredients, simplifying the fraction to 1/4 clarifies that flour constitutes one-quarter of the total ingredients.
-
Construction and Engineering: Precise measurements are critical in construction and engineering projects. Simplifying fractions helps ensure accuracy in calculations related to proportions, ratios, and measurements.
-
Finance and Budgeting: Managing personal finances and investments involves working with percentages and ratios. Understanding fraction simplification allows for easier analysis of financial data.
-
Data Analysis: In data analysis and statistics, fractions are frequently encountered when dealing with proportions and probabilities. Simplifying fractions helps present data in a more concise and understandable manner.
Beyond Simplification: Decimal and Percentage Representation
The simplified fraction 1/4 can also be represented as a decimal and a percentage:
-
Decimal: To convert a fraction to a decimal, divide the numerator by the denominator: 1 ÷ 4 = 0.25
-
Percentage: To convert a fraction to a percentage, multiply the decimal by 100: 0.25 x 100 = 25%
Further Exploration: Improper Fractions and Mixed Numbers
While 54/216 is a proper fraction (numerator < denominator), it's important to understand improper fractions (numerator ≥ denominator) and mixed numbers (a whole number and a proper fraction). An improper fraction can be converted to a mixed number by dividing the numerator by the denominator. The quotient is the whole number part, and the remainder becomes the numerator of the proper fraction part. Conversely, a mixed number can be converted back to an improper fraction.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 54/216?
A1: The simplest form of 54/216 is 1/4.
Q2: How do I find the greatest common divisor (GCD)?
A2: You can find the GCD using several methods: listing factors, prime factorization, or the Euclidean algorithm. The Euclidean algorithm is generally the most efficient for larger numbers.
Q3: Are 54/216 and 1/4 equivalent fractions?
A3: Yes, 54/216 and 1/4 are equivalent fractions. They represent the same value.
Q4: What are some real-world applications of simplifying fractions?
A4: Simplifying fractions has practical applications in various fields, including cooking, construction, finance, and data analysis, where precise measurements and proportions are essential.
Q5: How do I convert a fraction to a decimal and a percentage?
A5: To convert a fraction to a decimal, divide the numerator by the denominator. To convert a fraction to a percentage, multiply the resulting decimal by 100.
Conclusion: Mastering Fractions for Real-World Success
Understanding the fraction 54/216, its simplification to 1/4, and the broader concepts of equivalent fractions, GCD, and different representational forms (decimals and percentages) is crucial for various aspects of life. From everyday tasks like cooking to complex calculations in engineering and finance, the ability to work with fractions effectively is invaluable. This article aimed to provide a comprehensive understanding of these fundamental mathematical principles, empowering you to tackle similar problems with confidence. Remember, practice is key to mastering fractions. The more you work with them, the more intuitive and effortless the process will become.
Latest Posts
Latest Posts
-
Face Paint Green
Sep 17, 2025
-
82 5kg In Pounds
Sep 17, 2025
-
8 Of 2500
Sep 17, 2025
-
68inches In Cm
Sep 17, 2025
-
Slide Board Transfer
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 54 Of 216 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.