52 X 4
stanleys
Sep 11, 2025 · 6 min read
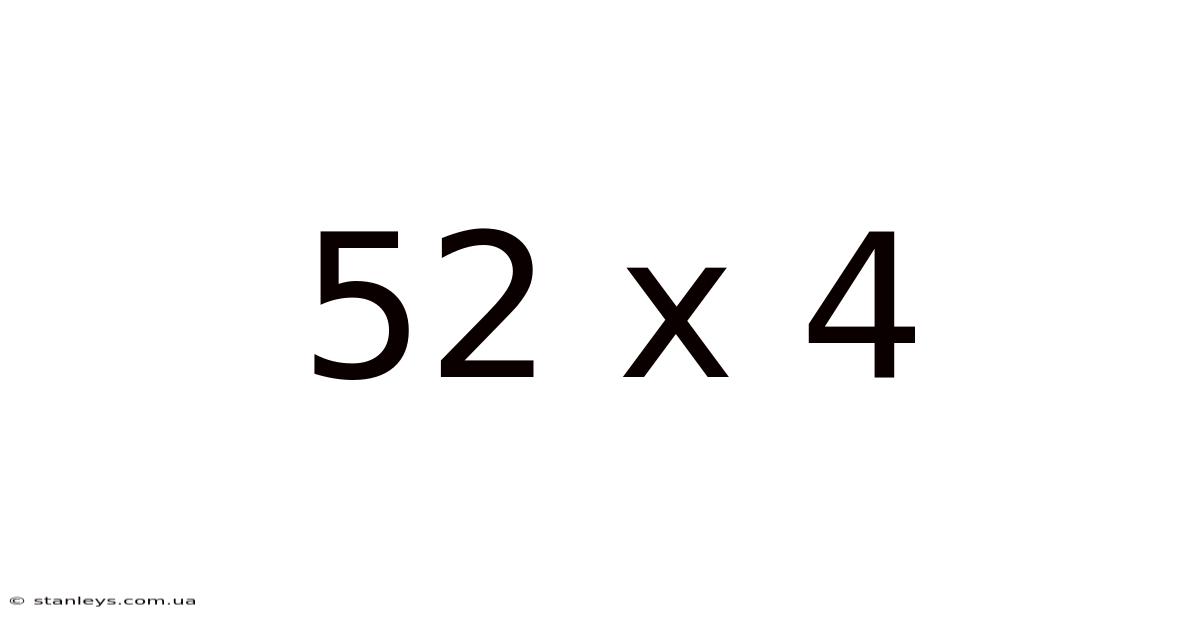
Table of Contents
Decoding 52 x 4: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 52 x 4, transforming it into a gateway to understanding fundamental mathematical concepts, practical applications, and even the history of multiplication itself. We'll delve beyond the simple answer, examining different methods of calculation, exploring the underlying principles, and demonstrating its relevance in various real-world scenarios. This comprehensive guide is perfect for students, educators, and anyone interested in sharpening their mathematical skills and appreciating the beauty of numbers.
Introduction: More Than Just a Calculation
The seemingly straightforward equation, 52 x 4, offers a fertile ground for exploring various mathematical concepts. It's not merely about finding the product; it's about understanding the process, exploring alternative approaches, and grasping the broader implications of multiplication within a wider mathematical context. This exploration will cover multiple methods of solving the problem, highlighting their strengths and weaknesses, and demonstrating their applicability in different contexts. We will also explore the historical context of multiplication, tracing its evolution from ancient civilizations to modern computational methods.
Method 1: Standard Multiplication Algorithm
The most common method taught in schools is the standard multiplication algorithm. This involves multiplying each digit of the multiplicand (52) by each digit of the multiplier (4) and then adding the partial products.
- Step 1: Multiply the ones digit of 52 (2) by 4: 2 x 4 = 8.
- Step 2: Multiply the tens digit of 52 (5) by 4: 5 x 4 = 20.
- Step 3: Add the partial products: 200 + 8 = 208.
Therefore, 52 x 4 = 208. This method is efficient for relatively small numbers and provides a systematic approach that is easily understood and applied.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down the problem into smaller, more manageable parts.
- Step 1: Rewrite 52 as 50 + 2.
- Step 2: Apply the distributive property: 4(50 + 2) = 4(50) + 4(2).
- Step 3: Calculate the individual products: 4(50) = 200 and 4(2) = 8.
- Step 4: Add the results: 200 + 8 = 208.
Thus, using the distributive property, we arrive at the same answer: 208. This method emphasizes the underlying mathematical principles and can be more intuitive for some learners.
Method 3: Repeated Addition
Multiplication can be visualized as repeated addition. This method is particularly helpful for beginners as it directly connects multiplication to a more familiar concept.
52 x 4 is equivalent to adding 52 four times: 52 + 52 + 52 + 52 = 208. While straightforward, this method becomes less efficient as the numbers involved increase in size. However, it provides a strong visual and conceptual understanding of the multiplication process.
Method 4: Lattice Multiplication
Lattice multiplication, a historical method, uses a grid to organize the multiplication process. It can be particularly helpful for larger numbers and provides a visual representation of the partial products.
- Draw a grid with two rows (for the two digits of 52) and one column (for the single digit of 4).
- Multiply each digit of 52 by 4 and write the result in the corresponding cell, separating tens and ones digits diagonally.
- Sum the diagonals, starting from the lower right. The sum of each diagonal represents a digit in the final answer.
This method, although seemingly more complex initially, offers a systematic way to handle multi-digit multiplication and aids in understanding the place value system.
The Historical Context of Multiplication
Multiplication, far from being a modern invention, has ancient roots. Evidence suggests that various forms of multiplication were used in ancient civilizations, including the Egyptians, Babylonians, and Greeks. The Egyptians used a doubling method, essentially a form of repeated addition, while the Babylonians utilized a sexagesimal (base-60) system. The Greeks employed geometrical methods and the development of algorithms continued throughout history, leading to the methods we use today. Understanding this historical perspective illuminates the evolution of mathematical thought and the gradual refinement of calculation techniques.
Real-World Applications of 52 x 4 (and Multiplication in General)
The seemingly simple calculation 52 x 4 has numerous real-world applications. Consider these examples:
- Calculating Costs: If a pack of pens costs $52 and you need 4 packs, the total cost is 52 x 4 = $208.
- Measuring Quantities: If a box contains 52 items and you have 4 boxes, you have a total of 208 items.
- Area Calculation: If a rectangular area measures 52 units by 4 units, its area is 208 square units.
- Time Calculation: If an activity takes 52 minutes and you repeat it 4 times, the total time is 208 minutes.
These are just a few examples. Multiplication is fundamental to countless aspects of daily life, from calculating financial transactions to understanding spatial relationships and managing resources. Mastering multiplication is key to navigating many aspects of the modern world.
Expanding the Concept: Beyond 52 x 4
The principles learned by solving 52 x 4 are applicable to a wide range of multiplication problems. The techniques discussed—standard algorithm, distributive property, repeated addition, and lattice multiplication—can be adapted to handle larger numbers and more complex calculations. Understanding these fundamental principles allows for the efficient and accurate calculation of any multiplication problem. It lays the foundation for more advanced mathematical concepts, including algebra, calculus, and beyond.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 52 x 4?
- A: The easiest method depends on individual preference and mathematical skill. The standard algorithm is generally efficient and widely taught, while repeated addition provides a strong conceptual understanding. The distributive property can also be easily grasped for this specific problem.
-
Q: Why is multiplication important?
- A: Multiplication is a fundamental operation used extensively in daily life, science, engineering, finance, and many other fields. It's a building block for more advanced mathematical concepts and is essential for solving a vast array of problems.
-
Q: Are there any other methods for solving multiplication problems?
- A: Yes, there are various other methods, including using multiplication tables, mental math techniques, and even using calculators or computer programs. The choice of method often depends on the complexity of the problem and the resources available.
-
Q: How can I improve my multiplication skills?
- A: Practice is key. Regularly solving multiplication problems, using different methods, and applying multiplication to real-world scenarios will significantly improve your skills. Using flashcards, online games, and working through practice exercises are also effective strategies.
Conclusion: The Enduring Significance of 52 x 4
This detailed exploration of 52 x 4 demonstrates that even seemingly simple mathematical problems offer profound opportunities for learning and understanding. By examining different calculation methods, exploring the historical context, and highlighting real-world applications, we’ve moved beyond a simple answer to uncover the rich tapestry of mathematical concepts embedded within this equation. The skills and understanding gained extend far beyond this specific problem, providing a solid foundation for more complex mathematical endeavors and enhancing one's ability to navigate the quantitative aspects of the world around us. The seemingly simple equation, 52 x 4, becomes a powerful tool for understanding the beauty and practicality of mathematics.
Latest Posts
Latest Posts
-
Anglo Saxon Photos
Sep 12, 2025
-
330ml In L
Sep 12, 2025
-
32cm To Mm
Sep 12, 2025
-
65 Of 60
Sep 12, 2025
-
27cm To Inches
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 52 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.