50 / 3
stanleys
Sep 11, 2025 · 6 min read
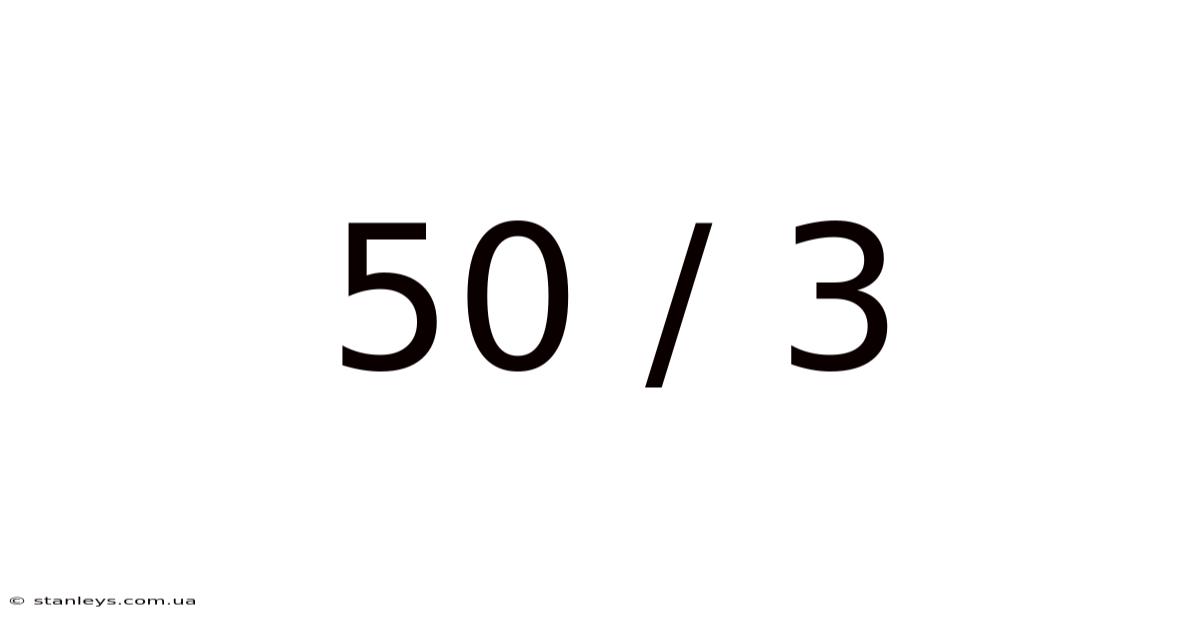
Table of Contents
Unveiling the Mystery: A Deep Dive into 50/3
The seemingly simple division problem, 50/3, hides a wealth of mathematical concepts and practical applications. This seemingly straightforward calculation offers a gateway to exploring fractions, decimals, remainders, and even the fascinating world of infinite series. This article will comprehensively examine 50/3, unpacking its various representations and exploring its implications within different mathematical contexts.
Introduction: Beyond the Obvious Answer
At first glance, 50 divided by 3 might appear trivial. A quick calculation using a calculator yields approximately 16.666666..., a seemingly endless string of sixes. However, this seemingly simple result unlocks a deeper understanding of fundamental mathematical principles. This article will explore the various ways to represent the answer, examining the fraction, decimal, and remainder forms and exploring their practical applications. We will also delve into the theoretical implications, looking at how this division problem illustrates core concepts in arithmetic and beyond.
Methods of Calculating 50/3
There are several ways to approach the calculation of 50/3. Let's explore the most common methods:
-
Long Division: This classic method provides a step-by-step approach to understanding the division process. We start by dividing 50 by 3. 3 goes into 5 once (3 x 1 = 3), leaving a remainder of 2. We bring down the 0, making it 20. 3 goes into 20 six times (3 x 6 = 18), leaving a remainder of 2. This process repeats indefinitely, resulting in the repeating decimal 16.666...
-
Using Fractions: Instead of a decimal, we can express the result as a mixed number. 3 goes into 50 sixteen times with a remainder of 2. Therefore, 50/3 can be expressed as 16 2/3. This fractional representation is precise and avoids the limitations of representing the infinite decimal expansion.
-
Calculator: The easiest way to find an approximate answer is to use a calculator. Inputting 50 ÷ 3 will yield the decimal approximation 16.666666..., which, while convenient, hides the underlying mathematical structure.
Understanding the Remainder: A Crucial Concept
The remainder in the division of 50 by 3 is 2. This seemingly small number holds significant meaning. It indicates that 50 is not perfectly divisible by 3. It signifies that there are two units left over after distributing 50 items into groups of 3. This concept of remainders is crucial in various applications, from scheduling tasks evenly to understanding modular arithmetic. For example, in a calendar, if you need to schedule a task every 3 days, knowing the remainder helps determine when the cycle will restart.
The Decimal Expansion: A Repeating Decimal
The decimal representation of 50/3 (16.666...) is a repeating decimal, meaning the digit 6 repeats infinitely. This repeating pattern is not a coincidence; it's a direct consequence of the fact that 50/3 cannot be expressed as a terminating decimal. Understanding repeating decimals is crucial for working with fractions and understanding the limitations of decimal representation. Many fractions, when converted to decimals, will result in repeating or terminating decimal representations. Those that repeat infinitely are called rational numbers, while those that do not repeat infinitely, like π (pi), are irrational numbers.
Applications of 50/3 and Related Concepts
The principles illustrated by the division 50/3 find application in various fields:
-
Real-world Division Problems: Imagine distributing 50 candies evenly among 3 friends. Each friend gets 16 candies, and you have 2 candies left over. This simple scenario highlights the practical relevance of understanding remainders.
-
Modular Arithmetic: In computer science and cryptography, modular arithmetic plays a vital role. The remainder after division is crucial in these calculations. For example, determining if a number is even or odd uses modular arithmetic with a modulus of 2. The remainder when a number is divided by 3 is used similarly.
-
Fractions and Ratio in Everyday Life: Understanding fractions is essential in countless everyday scenarios – cooking, construction, sewing, and so on. Working with fractions effectively requires a strong grasp of division and remainders. Expressing 50/3 as 16 2/3 allows for easier manipulation in practical calculations.
-
Engineering and Measurement: In fields requiring precise measurements, understanding fractions and decimals is crucial. Converting between fractional and decimal representations might be necessary to ensure accuracy. This division is similar to cutting a 50-meter rope into 3 equal pieces where precision is important.
-
Finance: Dividing profits, splitting expenses, or calculating interest rates often involves division, sometimes leading to decimal or fractional amounts that must be managed carefully.
Exploring Further: Infinite Series and Continued Fractions
The repeating decimal 16.666... can be expressed as an infinite geometric series: 16 + 6/10 + 6/100 + 6/1000 + ... This series provides another way to understand the value of 50/3, connecting the decimal expansion to the concept of infinite series, a powerful tool in calculus and other advanced mathematical areas.
Furthermore, 50/3 can also be represented as a continued fraction. A continued fraction is a way of representing a number as a fraction within a fraction, and so on. While the process for generating the continued fraction for 50/3 is somewhat more advanced, it illustrates another powerful representation of numbers, showing that even seemingly simple numbers can have intricate mathematical expressions.
Frequently Asked Questions (FAQ)
-
Q: What is the exact value of 50/3?
- A: The exact value is 16 2/3. The decimal representation 16.666... is an approximation.
-
Q: Why does 50/3 result in a repeating decimal?
- A: Because 3 is not a factor of 50, the division results in a remainder that continues to generate repeating digits.
-
Q: How can I convert 16 2/3 to a decimal?
- A: Convert the fraction 2/3 to a decimal (0.666...). Then add it to 16, resulting in 16.666...
-
Q: What are some real-world examples where I might encounter this type of division?
- A: Dividing resources among people, calculating unit costs, splitting bills, and various aspects of measurement.
-
Q: Is there a way to express 50/3 without using decimals or fractions?
- A: No, the precise representation of 50/3 necessitates either a fraction (16 2/3) or a repeating decimal (16.666...).
Conclusion: The Richness of a Simple Problem
The seemingly simple calculation of 50/3 reveals a surprising depth of mathematical concepts. From the practical application of remainders to the theoretical exploration of repeating decimals and infinite series, this seemingly basic division problem offers a rich tapestry of mathematical insights. Understanding the different ways to represent and interpret this calculation strengthens foundational mathematical skills and provides a gateway to appreciating the elegance and power of mathematics in various contexts. By delving into the intricacies of this simple problem, we gain a deeper understanding of the fundamental building blocks of arithmetic and their far-reaching applications. This exploration highlights the importance of not just finding an answer, but understanding the underlying mathematical principles that govern the solution.
Latest Posts
Latest Posts
-
250ml To Oz
Sep 11, 2025
-
18 X 5
Sep 11, 2025
-
52 5kg In Stone
Sep 11, 2025
-
Thy Hand Belinda
Sep 11, 2025
-
86 6kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 50 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.