5 X 3/2
stanleys
Sep 12, 2025 · 6 min read
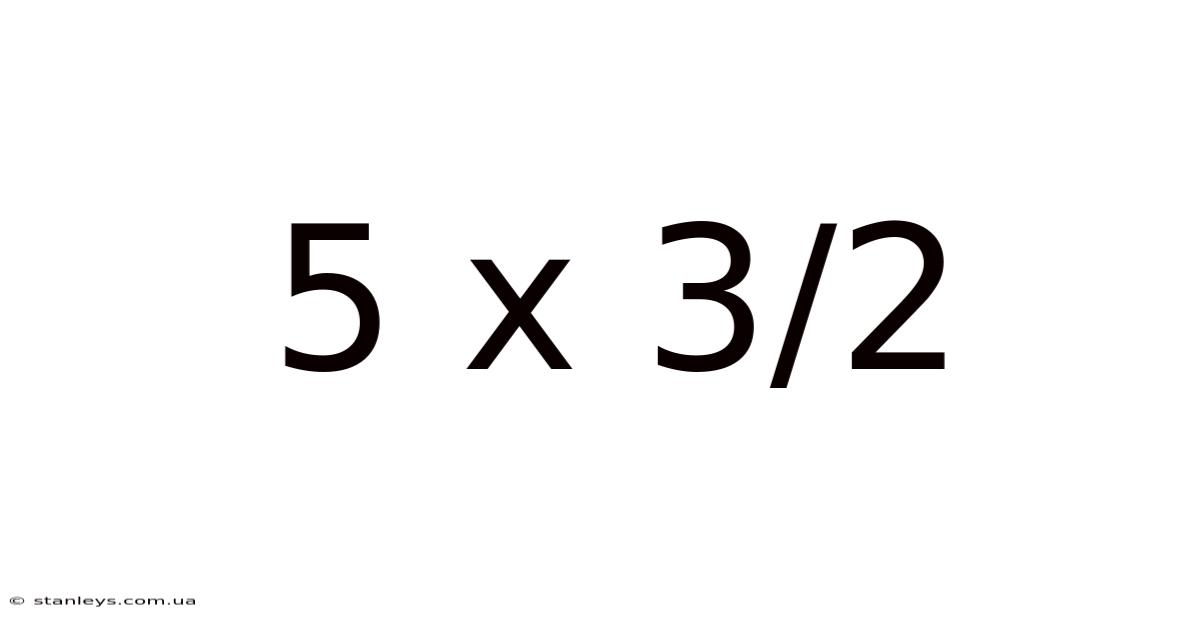
Table of Contents
Decoding 5 x 3/2: A Deep Dive into Mathematical Operations
This article explores the seemingly simple mathematical expression "5 x 3/2," providing a comprehensive understanding of its solution and the underlying principles involved. We'll delve into the order of operations, different approaches to solving the problem, and explore the broader mathematical concepts it represents. Understanding this seemingly basic calculation opens doors to a deeper appreciation of arithmetic and its applications. We’ll cover everything from basic multiplication and division to more advanced concepts, making this a valuable resource for students and anyone looking to refresh their mathematical skills.
Introduction: Understanding the Order of Operations
Before we tackle "5 x 3/2," let's establish a crucial foundation: the order of operations. This set of rules dictates the sequence in which we perform different mathematical operations within an expression. It's often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same fundamental principles. The key takeaway is that multiplication and division have equal precedence and are performed from left to right, as are addition and subtraction.
This means that in the expression "5 x 3/2," we don't simply multiply 5 by 3 and then divide by 2. Instead, we proceed from left to right, performing the multiplication before the division.
Step-by-Step Solution: Solving 5 x 3/2
Let's break down the solution step-by-step:
-
Multiplication First: The first operation is 5 x 3, which equals 15.
-
Division: Now we have 15 / 2. This results in 7.5 or 7 ½.
Therefore, the answer to 5 x 3/2 is 7.5.
Alternative Approaches and Interpretations
While the left-to-right approach is standard and crucial for consistent results, let's examine a slightly different perspective. Some might interpret the expression as 5 x (3/2). This introduces parentheses, altering the order of operations.
-
Parentheses First: We tackle the parentheses first: 3/2 = 1.5
-
Multiplication: Then, we multiply 5 by 1.5, which also equals 7.5.
This demonstrates that in this specific case, regardless of whether we implicitly or explicitly group the division, the outcome remains consistent. However, this is not always the case in more complex mathematical expressions. The importance of adhering strictly to PEMDAS/BODMAS for accuracy becomes increasingly clear as we work with more intricate equations.
The Importance of Fraction Understanding
The expression "5 x 3/2" highlights the fundamental importance of understanding fractions. A fraction represents a part of a whole. In this case, 3/2 signifies one and a half (or 1.5 in decimal form). Understanding fractional arithmetic is crucial for tackling more complex calculations involving ratios, proportions, and algebraic manipulations.
The multiplication of 5 by 3/2 can also be visualized as finding the area of a rectangle with sides of length 5 and 3/2 units. This geometric interpretation provides a tangible representation of the mathematical operation and can improve understanding for visual learners.
Expanding the Concept: Applications in Real-World Scenarios
The seemingly simple calculation "5 x 3/2" has surprising applications in various real-world scenarios. Here are a few examples:
-
Calculating Ingredient Quantities: In cooking or baking, scaling recipes often involves multiplying fractions. If a recipe calls for 3/2 cups of flour and you want to make five times the quantity, the calculation becomes 5 x 3/2, leading to 7.5 cups of flour.
-
Determining Unit Cost: If five identical items cost a total of 15 units of currency, the cost per item can be determined using division. This is the reverse of our example: 15 / 5 = 3. Then, to find the cost of 3/2 items, we’d do 3 x (3/2) = 4.5 units of currency.
-
Calculating Areas and Volumes: Many geometric calculations involve multiplying fractions and whole numbers. Imagine calculating the area of a triangle with a base of 5 units and a height of 3/2 units, for instance. The formula (1/2) * base * height would lead us directly to our original equation in a practical application.
-
Physics and Engineering: This type of calculation is commonplace in physics and engineering problems, including force calculations, energy calculations, and the determination of physical quantities in various contexts.
Moving Beyond the Basics: Extending the Concepts
The principles demonstrated in solving "5 x 3/2" serve as building blocks for more advanced mathematical concepts. These include:
-
Algebra: The ability to manipulate equations and solve for unknowns relies heavily on understanding the order of operations and working with fractions.
-
Calculus: Understanding fractions and manipulating expressions is fundamental to calculus, where derivatives and integrals involve complex calculations involving numerous operations and fractions.
-
Linear Algebra: Linear algebra, a cornerstone of many advanced mathematical applications, frequently employs matrix operations and linear equations, all of which build upon fundamental arithmetic skills like those highlighted in this problem.
Frequently Asked Questions (FAQ)
Q: What if the expression was written as 5 x (3/2)? Would the answer change?
A: No, the answer would remain the same (7.5). The parentheses explicitly show the division must be performed before the multiplication. However, as previously stated, in cases with more complex equations, parentheses are crucial for ensuring correct order of operation.
Q: Can I convert the fraction to a decimal before performing the calculation?
A: Yes, absolutely! Converting 3/2 to 1.5 beforehand is perfectly acceptable. This would transform the expression into 5 x 1.5, which still results in 7.5.
Q: Are there any other ways to solve this equation?
A: While the left-to-right method is the most efficient and generally recommended approach, other methods might involve factoring or using alternative algebraic manipulations. For this particular equation, the left-to-right method using PEMDAS/BODMAS is the most streamlined approach.
Q: Why is the order of operations so important?
A: The order of operations ensures consistency and accuracy in mathematical calculations. Without a standardized order, different individuals could obtain different results for the same expression, leading to confusion and errors.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation of "5 x 3/2" encapsulates crucial mathematical concepts—the order of operations, fraction understanding, and the ability to manipulate numbers efficiently. Mastering these fundamentals forms the bedrock for tackling more complex mathematical problems. Whether you’re a student striving for academic excellence or an adult looking to refresh your mathematical skills, a firm grasp of these principles is indispensable. This example demonstrates that even basic mathematical operations can offer insights into the intricacies and elegance of mathematics, laying a strong foundation for future mathematical exploration. The consistent application of the order of operations guarantees accurate results and fosters a deeper understanding of the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Victorian Era Cosmetics
Sep 12, 2025
-
Anti Bumping Granules
Sep 12, 2025
-
Cool Runnings Quotes
Sep 12, 2025
-
How Your Today
Sep 12, 2025
-
Micrometers To Centimeters
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 5 X 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.