5/9 In Decimal
stanleys
Sep 13, 2025 · 5 min read
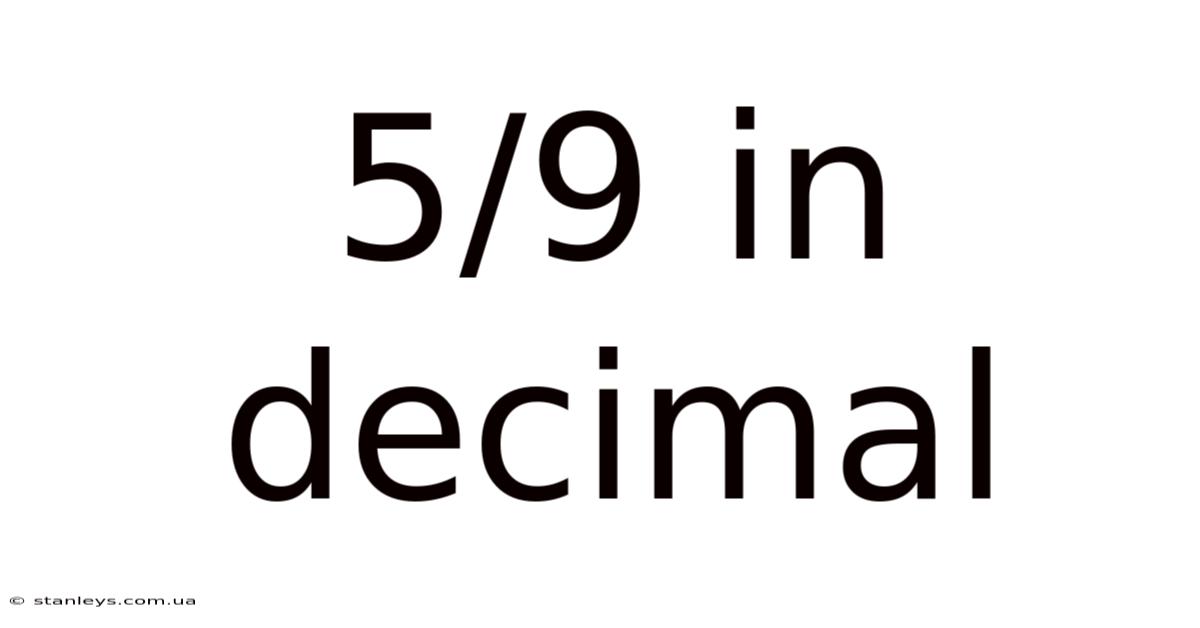
Table of Contents
Decoding 5/9: A Comprehensive Guide to Converting Fractions to Decimals
Understanding fractions and decimals is fundamental to mathematics and numerous real-world applications. This comprehensive guide will delve into the conversion of the fraction 5/9 into its decimal equivalent, exploring the process, its significance, and related concepts. We'll cover various methods for conversion, address common misconceptions, and provide practical examples to solidify your understanding. By the end, you'll not only know the decimal value of 5/9 but also possess a robust grasp of fractional and decimal representations.
Introduction: Fractions and Decimals – A Symbiotic Relationship
Fractions and decimals represent parts of a whole. A fraction expresses a part as a ratio of two integers (numerator and denominator), while a decimal expresses a part using base-ten notation, employing a decimal point to separate the whole number part from the fractional part. The ability to convert between these two representations is crucial for various mathematical operations and problem-solving. The fraction 5/9, for example, represents five parts out of nine equal parts of a whole. Converting this fraction to a decimal allows for easier comparison with other decimals and simplifies calculations in certain contexts.
Method 1: Long Division – The Fundamental Approach
The most fundamental method for converting a fraction to a decimal is long division. To convert 5/9 to a decimal, we perform the division: 5 ÷ 9.
-
Set up the division: Write 5 as the dividend (inside the division symbol) and 9 as the divisor (outside). Add a decimal point followed by zeros to the dividend (5.0000...). This allows us to continue the division process indefinitely.
-
Perform the division: 9 does not go into 5, so we add a zero to the dividend, making it 50. 9 goes into 50 five times (9 x 5 = 45). Subtract 45 from 50, leaving a remainder of 5.
-
Continue the process: Bring down the next zero (making it 50 again). Repeat the process: 9 goes into 50 five times (45). Subtract 45, leaving a remainder of 5.
-
Observe the pattern: Notice that the remainder is consistently 5. This indicates a repeating decimal. The quotient will continue with the digit 5 indefinitely.
-
Represent the repeating decimal: We represent the repeating decimal using a bar over the repeating digit(s). Therefore, 5/9 = 0.5555... = 0.$\overline{5}$.
Method 2: Utilizing Decimal Equivalents of Common Fractions
While long division is fundamental, recognizing common fraction-to-decimal equivalents can expedite the process. While 5/9 isn't among the most frequently memorized, understanding the pattern of ninths can be helpful.
Let's look at the decimal equivalents of fractions with a denominator of 9:
- 1/9 = 0.$\overline{1}$
- 2/9 = 0.$\overline{2}$
- 3/9 = 0.$\overline{3}$
- 4/9 = 0.$\overline{4}$
- 5/9 = 0.$\overline{5}$
- 6/9 = 0.$\overline{6}$
- 7/9 = 0.$\overline{7}$
- 8/9 = 0.$\overline{8}$
- 9/9 = 1.0
Observe the pattern: The numerator of the fraction directly corresponds to the repeating digit in the decimal representation. This pattern holds true for all fractions with a denominator of 9 (excluding 9/9, which equals 1).
Understanding Repeating Decimals
The decimal representation of 5/9, 0.$\overline{5}$, is a repeating decimal or recurring decimal. This means that the digit 5 repeats infinitely. Not all fractions result in repeating decimals. Fractions whose denominators have only 2 and/or 5 as prime factors will result in terminating decimals (decimals that end after a finite number of digits). For example, 1/4 = 0.25, and 1/10 = 0.1.
The Significance of Repeating Decimals in Mathematics
Repeating decimals are ubiquitous in mathematics. They arise frequently in calculations involving fractions and irrational numbers. Understanding their properties is essential for various mathematical operations, such as addition, subtraction, multiplication, and division of decimals. They also play a crucial role in advanced mathematical concepts like series and limits.
Practical Applications of Decimal Representation
The decimal representation of 5/9, and fraction-to-decimal conversions in general, are indispensable in many real-world applications:
-
Measurements: Converting fractional measurements (e.g., 5/9 of an inch) to decimal form is often necessary for precise calculations in engineering, construction, and manufacturing.
-
Financial calculations: Decimals are crucial for calculations involving money, percentages, interest rates, and other financial aspects.
-
Scientific calculations: Many scientific calculations involve fractions and decimals, particularly in fields like physics, chemistry, and engineering.
-
Data analysis: Representing data in decimal form facilitates comparisons and analysis, particularly in statistical applications.
Frequently Asked Questions (FAQ)
Q: Can 5/9 be expressed as a terminating decimal?
A: No, 5/9 cannot be expressed as a terminating decimal. It results in a repeating decimal, 0.$\overline{5}$, because its denominator (9) contains prime factors other than 2 and 5.
Q: How can I convert other fractions to decimals?
A: Use the long division method. Divide the numerator by the denominator. If the division doesn't terminate, you'll have a repeating decimal. Alternatively, if you recognize common fraction-decimal equivalents, you can use that knowledge to simplify the conversion.
Q: What is the difference between a rational and an irrational number?
A: A rational number can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Rational numbers can be represented as either terminating or repeating decimals. An irrational number cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal representation (e.g., π, √2).
Q: Are there any shortcuts for converting fractions with a denominator of 9?
A: Yes, as demonstrated earlier, for fractions with a denominator of 9, the numerator directly corresponds to the repeating digit in the decimal representation (e.g., 7/9 = 0.$\overline{7}$).
Conclusion: Mastering Fractions and Decimals
The conversion of 5/9 to its decimal equivalent, 0.$\overline{5}$, highlights the fundamental relationship between fractions and decimals. Understanding this conversion process, including the long division method and recognizing patterns in repeating decimals, is crucial for various mathematical applications and real-world scenarios. By mastering these concepts, you'll enhance your mathematical skills and gain a more profound understanding of numerical representation. Remember that practice is key to solidifying this knowledge. Work through various fraction-to-decimal conversions to build confidence and proficiency. The more you practice, the easier and more intuitive these conversions will become.
Latest Posts
Latest Posts
-
Aquarius Constellation Tattoo
Sep 13, 2025
-
75 6kg In Stone
Sep 13, 2025
-
800m In Kilometres
Sep 13, 2025
-
3 4 6
Sep 13, 2025
-
18 5 Of 964
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5/9 In Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.