5/18 Of 3
stanleys
Sep 13, 2025 · 5 min read
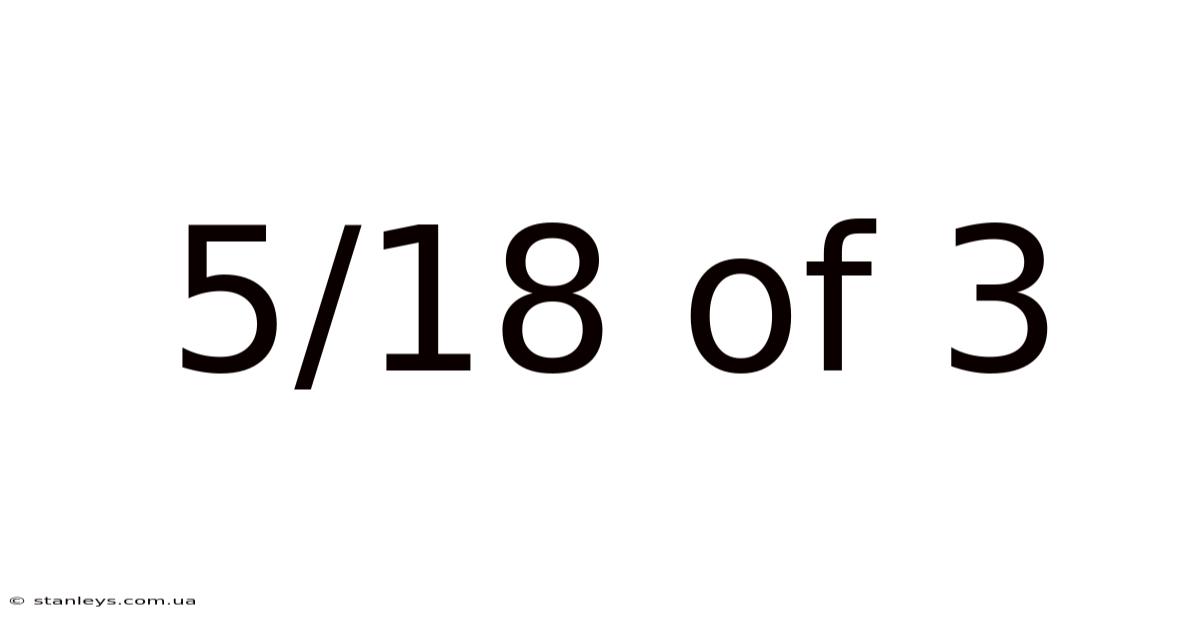
Table of Contents
Decoding 5/18 of 3: A Comprehensive Guide to Fractions and Multiplication
Understanding fractions and their application in multiplication is a fundamental concept in mathematics. This article will provide a comprehensive exploration of the problem "5/18 of 3," breaking down the process step-by-step, explaining the underlying principles, and addressing common questions and misconceptions. We'll go beyond simply finding the answer to build a solid understanding of fractional multiplication.
Introduction: Understanding the Problem
The phrase "5/18 of 3" represents a multiplication problem involving a fraction (5/18) and a whole number (3). It asks us to find what portion of 3 is represented by 5/18. This type of problem appears frequently in various mathematical contexts, from everyday calculations to more complex scientific and engineering applications. Mastering this concept is key to success in many areas of mathematics. This guide will not only solve the problem but also equip you with the skills to tackle similar fractional multiplication problems with confidence.
Step-by-Step Solution: Calculating 5/18 of 3
To solve "5/18 of 3," we translate the phrase "of" into multiplication. Therefore, the problem becomes: (5/18) * 3. We can solve this problem using several methods:
Method 1: Multiplying the Numerator and Keeping the Denominator
This is the most straightforward method. We multiply the numerator of the fraction (5) by the whole number (3), keeping the denominator (18) unchanged.
- Multiplication: 5 * 3 = 15
- Result: The result is 15/18
This fraction can be further simplified.
Method 2: Converting the Whole Number to a Fraction
We can express the whole number 3 as a fraction with a denominator of 1 (3/1). This allows us to multiply two fractions directly.
- Rewrite 3 as a fraction: 3 = 3/1
- Multiplication of fractions: (5/18) * (3/1) = (5 * 3) / (18 * 1) = 15/18
Again, we obtain the fraction 15/18.
Simplifying the Fraction: Finding the Lowest Common Denominator
Both methods yield the fraction 15/18. However, this fraction can be simplified by finding the greatest common divisor (GCD) of the numerator (15) and the denominator (18). The GCD of 15 and 18 is 3. We divide both the numerator and the denominator by 3:
- Divide the numerator by the GCD: 15 ÷ 3 = 5
- Divide the denominator by the GCD: 18 ÷ 3 = 6
- Simplified fraction: 5/6
Therefore, 5/18 of 3 is equal to 5/6.
Method 3: Using Cancellation (For More Complex Problems)
Cancellation is a powerful technique to simplify calculations before performing the multiplication. This method is particularly useful when dealing with larger numbers or more complex fractions. In this case:
- Identify common factors: Notice that 3 is a factor of both the numerator (in 3/1) and the denominator (18).
- Cancel the common factor: Divide 3 (the numerator of 3/1) by 3 and divide 18 (the denominator of 5/18) by 3. This leaves us with: (5/6) * (1/1) = 5/6.
Cancellation simplifies the calculation significantly, especially with larger numbers.
Understanding the Result: What Does 5/6 Represent?
The final answer, 5/6, represents five-sixths of the whole number 3. Imagine dividing 3 into six equal parts. Each part would represent 3/6, or 1/2. The answer, 5/6, indicates that we are considering five of these six parts.
Visual Representation: Making it Concrete
Imagine a pizza cut into six slices. "5/18 of 3" means taking five slices from three pizzas that have been cut into eighteen slices each. The total would still be 5/6 of a pizza. This visual helps in understanding the concept of fractions and their multiplication.
Explanation of the Underlying Mathematical Principles
The process of multiplying fractions involves multiplying the numerators together and the denominators together. This operation fundamentally represents the combination of parts of a whole.
- Numerator: Represents the number of parts we are considering.
- Denominator: Represents the total number of parts in the whole.
- Multiplication: Combining fractional parts.
Frequently Asked Questions (FAQs)
-
Q: What if the whole number was a fraction as well?
A: If the whole number were also a fraction, you would simply multiply the two fractions together using the same method as described above. For instance, (5/18) * (2/3) would be (52)/(183) = 10/54, which simplifies to 5/27.
-
Q: Is there a way to solve this without converting to fractions?
A: While the fractional method is the most common and reliable, you could interpret "5/18 of 3" as first finding 1/18 of 3 (which is 3/18 or 1/6) and then multiplying by 5, arriving at 5/6. This is essentially the same process, just presented differently.
-
Q: Why is simplification important?
A: Simplifying fractions helps to express the answer in its simplest form. It makes the result easier to understand and compare with other fractions. It also prevents potential errors in subsequent calculations.
-
Q: Can I use a calculator to solve this?
A: Yes, most calculators can handle fraction multiplication. However, understanding the underlying principles is crucial for applying this knowledge to various mathematical situations, which a calculator alone cannot teach.
Conclusion: Mastering Fractional Multiplication
Understanding "5/18 of 3" involves a fundamental application of fractional multiplication. By breaking down the problem into steps, understanding the mathematical principles, and utilizing simplification techniques, you can confidently solve similar problems. Mastering fractional multiplication lays a solid foundation for more advanced mathematical concepts. Remember to always simplify your answer to the lowest terms to present the most concise and accurate representation of the result. The key is not just to get the answer (5/6), but to understand why that's the answer and how to apply the same process to other similar problems. Practice is essential to build confidence and proficiency.
Latest Posts
Latest Posts
-
40 Of 1000
Sep 13, 2025
-
15 Off 85
Sep 13, 2025
-
Ethanol Ethanoic Acid
Sep 13, 2025
-
Fire Extinguishing Systems
Sep 13, 2025
-
Tennis Ball Dimensions
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 5/18 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.