42 In Binary
stanleys
Sep 18, 2025 · 6 min read
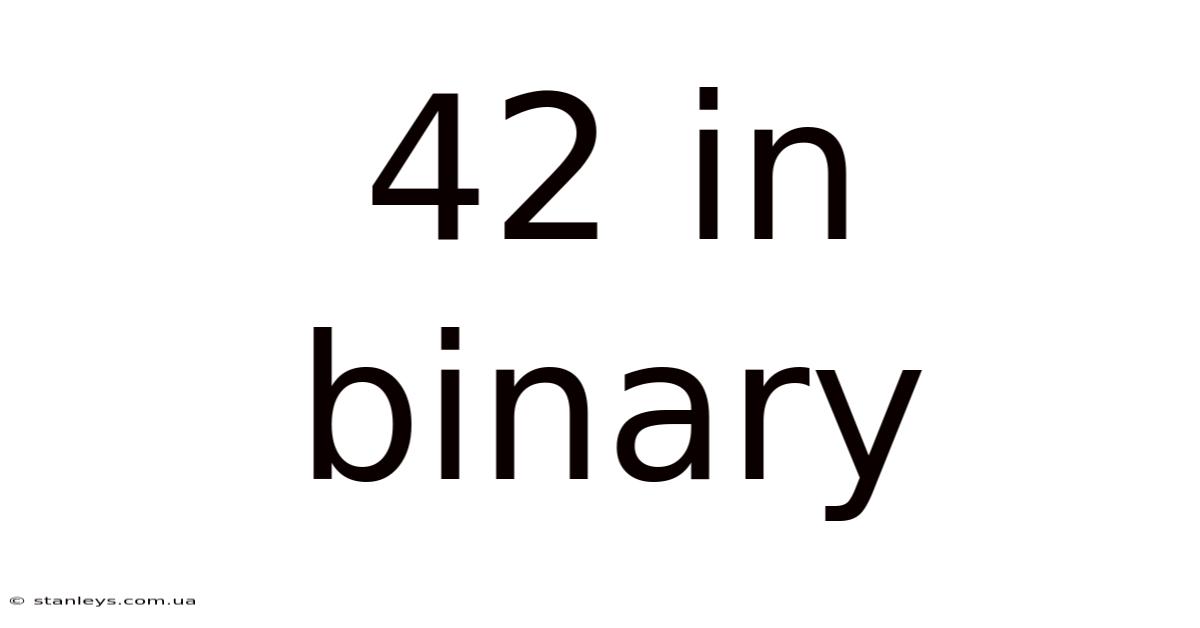
Table of Contents
Decoding 42: A Deep Dive into Binary Representation
The seemingly simple number 42 holds a special place in popular culture, famously representing "the answer to the ultimate question of life, the universe, and everything" in Douglas Adams' The Hitchhiker's Guide to the Galaxy. But beyond its literary significance, 42 also provides a fascinating opportunity to explore the fundamental concepts of binary code, the language of computers. This article will delve into the intricacies of representing 42 in binary, exploring the underlying principles and expanding on related topics like binary arithmetic and the significance of this numerical system in computing.
Understanding Binary Numbers: The Foundation of Computing
Before diving into the binary representation of 42, let's establish a foundational understanding of the binary number system. Unlike the decimal system (base-10) we use daily, which uses ten digits (0-9), the binary system (base-2) employs only two digits: 0 and 1. This simplicity is crucial for computers, as these two digits can be easily represented by the presence or absence of an electrical signal – a fundamental building block of digital electronics. Each digit in a binary number is called a bit (binary digit).
Think of it like this: in the decimal system, the position of a digit determines its value (e.g., in the number 123, the '1' represents 100, the '2' represents 20, and the '3' represents 3). Similarly, in the binary system, each position represents a power of 2. Starting from the rightmost position (the least significant bit), the positions represent 2<sup>0</sup> (1), 2<sup>1</sup> (2), 2<sup>2</sup> (4), 2<sup>3</sup> (8), and so on.
For example, the binary number 1011 is calculated as follows:
- 1 × 2<sup>3</sup> = 8
- 0 × 2<sup>2</sup> = 0
- 1 × 2<sup>1</sup> = 2
- 1 × 2<sup>0</sup> = 1
Adding these values together (8 + 0 + 2 + 1), we get 11 in decimal. Therefore, the binary number 1011 is equivalent to 11 in decimal.
Representing 42 in Binary: A Step-by-Step Conversion
Now, let's apply this understanding to convert the decimal number 42 into its binary equivalent. We can achieve this using several methods:
Method 1: Repeated Division by 2
This is a widely used method for converting decimal numbers to binary. The process involves repeatedly dividing the decimal number by 2 and recording the remainders. The remainders, read in reverse order, form the binary representation.
Let's convert 42:
- 42 ÷ 2 = 21, remainder 0
- 21 ÷ 2 = 10, remainder 1
- 10 ÷ 2 = 5, remainder 0
- 5 ÷ 2 = 2, remainder 1
- 2 ÷ 2 = 1, remainder 0
- 1 ÷ 2 = 0, remainder 1
Reading the remainders from bottom to top, we get 101010. Therefore, 42 in decimal is equivalent to 101010 in binary.
Method 2: Subtraction of Powers of 2
This method involves subtracting the largest possible power of 2 from the decimal number and repeating the process with the remainder until the remainder becomes 0.
- 42 - 32 (2<sup>5</sup>) = 10
- 10 - 8 (2<sup>3</sup>) = 2
- 2 - 2 (2<sup>1</sup>) = 0
This gives us 1 × 2<sup>5</sup> + 0 × 2<sup>4</sup> + 1 × 2<sup>3</sup> + 0 × 2<sup>2</sup> + 1 × 2<sup>1</sup> + 0 × 2<sup>0</sup> = 32 + 0 + 8 + 0 + 2 + 0 = 42. The binary representation is again 101010.
Beyond the Basics: Binary Arithmetic and Data Representation
Understanding binary representation is crucial for comprehending how computers perform calculations and store data. Computers perform arithmetic operations – addition, subtraction, multiplication, and division – using binary numbers. Let's explore some examples related to 42.
Binary Addition: Adding two binary numbers involves the same principles as decimal addition, but with only two digits. For example, let's add 42 (101010) and 10 (1010):
101010
+ 01010
---------
110000 (This is 48 in decimal)
Binary Subtraction: Binary subtraction also follows similar principles to decimal subtraction, involving borrowing from higher-order bits when necessary.
Data Representation: Computers represent various types of data, including numbers, text, images, and audio, using binary code. Each data type has its own specific encoding scheme. For instance, text is often represented using character encoding schemes like ASCII or Unicode, where each character is assigned a unique binary code. Images are represented using pixel data, where each pixel's color is encoded using binary numbers.
Frequently Asked Questions (FAQ)
Q: Why is binary code so important in computing?
A: Binary code is fundamental to computing because it directly maps to the on/off states of electronic switches within computer circuits. This simplicity allows for efficient and reliable processing of information.
Q: Are there other number systems used in computing besides binary?
A: Yes, while binary is the primary number system for computer hardware, other number systems like hexadecimal (base-16) and octal (base-8) are often used for representing binary data in a more human-readable format. Hexadecimal, for example, is frequently used in programming and computer science for representing memory addresses and color codes.
Q: Can I convert any decimal number to binary?
A: Yes, any decimal number, no matter how large or small (including negative numbers using techniques like two's complement), can be represented in binary.
Q: What about fractions and decimal points in binary?
A: Fractions and decimal points are also representable in binary, using a similar system to decimal representation, but with powers of 2 instead of powers of 10. For instance, 0.5 in decimal is 0.1 in binary (0.5 = 1 × 2<sup>-1</sup>).
Conclusion: The Significance of 42 (and Binary)
While 42's significance might stem from literature, its binary representation – 101010 – offers a concrete example of the fundamental principles underpinning modern computing. By understanding the conversion methods and the underlying concepts of binary arithmetic, we gain a deeper appreciation for the elegant simplicity of this system and its pervasive role in shaping our digital world. The seemingly simple number 42, therefore, becomes a gateway to a vast and complex universe of computational possibilities. From the simplest calculations to the most advanced algorithms, binary code forms the invisible backbone of everything digital, making it a crucial concept for anyone interested in understanding technology's inner workings. The journey from understanding the binary representation of 42 to grasping the broader concepts of binary arithmetic and data representation is a compelling example of how a single numerical value can unlock a profound understanding of a fundamental aspect of modern technology.
Latest Posts
Latest Posts
-
Bottomless Bucket Terraria
Sep 18, 2025
-
0 4as A Fraction
Sep 18, 2025
-
Infusion Rate Formula
Sep 18, 2025
-
Millicents Prosthesis Location
Sep 18, 2025
-
30 Of 16
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 42 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.