40 Of 240
stanleys
Sep 12, 2025 · 5 min read
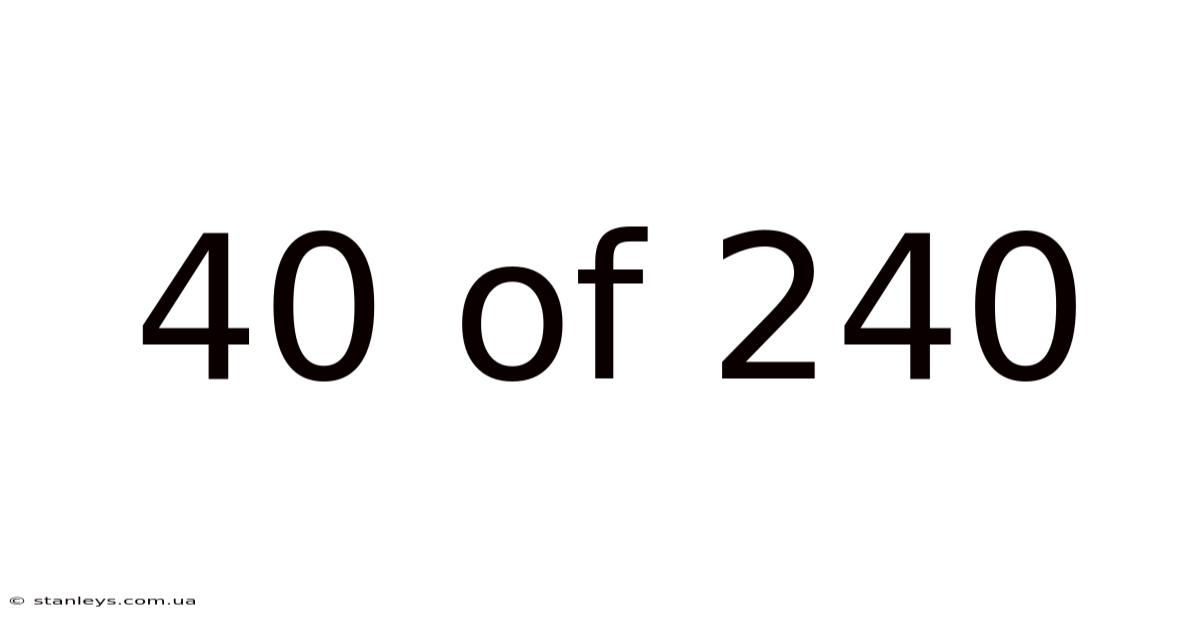
Table of Contents
Decoding the Mystery: Understanding 40 out of 240 (and its Implications)
Understanding the relationship between two numbers, particularly when one is a fraction of the other, is a fundamental skill in mathematics with far-reaching applications in various fields. This article delves into the meaning and implications of "40 out of 240," exploring its representation as a fraction, decimal, percentage, and its relevance in real-world scenarios. We'll also address common misconceptions and provide practical examples to solidify your understanding. This guide aims to empower you with a clear, comprehensive understanding of this seemingly simple yet powerful mathematical concept.
Representing 40 out of 240: Different Perspectives
The phrase "40 out of 240" signifies that 40 represents a portion of a larger whole, 240. This can be expressed in several ways, each offering a unique perspective:
1. Fraction: The most direct representation is as a fraction: 40/240. This fraction can be simplified by finding the greatest common divisor (GCD) of 40 and 240, which is 40. Dividing both the numerator and the denominator by 40, we get the simplified fraction 1/6. This means that 40 out of 240 is equivalent to one-sixth of the total.
2. Decimal: To convert the fraction 1/6 to a decimal, we perform the division: 1 ÷ 6 ≈ 0.1667. This decimal representation provides a numerical value for the proportion. Note that the decimal representation of 1/6 is a repeating decimal (0.1666...), and we often round it for practical purposes.
3. Percentage: To express the proportion as a percentage, we multiply the decimal by 100: 0.1667 × 100 ≈ 16.67%. This means that 40 out of 240 represents approximately 16.67% of the total.
Real-World Applications and Interpretations
The concept of "40 out of 240" finds applications in a wide array of situations. Let's explore some examples:
-
Test Scores: Imagine a student scored 40 out of 240 on a test. This translates to a score of 1/6 or approximately 16.67%. The interpretation depends on the context. Is this a good score? It depends on the grading scale and the difficulty of the test.
-
Sales Performance: A salesperson might have made 40 sales out of 240 potential clients. This represents a 16.67% conversion rate. This data is crucial for analyzing sales strategies and identifying areas for improvement.
-
Survey Results: In a survey of 240 people, 40 responded positively to a particular question. This indicates that 16.67% of respondents held that specific opinion. This percentage can inform decision-making processes.
-
Manufacturing Defects: If a factory produces 240 items and 40 are defective, this translates to a 16.67% defect rate. This high defect rate would necessitate immediate attention to improve quality control.
-
Project Completion: If a project involves 240 tasks, and 40 have been completed, then 1/6 or 16.67% of the project is finished. This allows for tracking progress and estimating remaining time.
Understanding Proportions and Ratios
The relationship between 40 and 240 is a ratio, expressed as 40:240. This ratio can be simplified to 1:6, demonstrating that for every one part, there are six parts in total. Understanding ratios is crucial in scaling recipes, mixing chemicals, and many other applications. Proportions, on the other hand, involve comparing two ratios. For example, if we know that the ratio of boys to girls in a class is 1:2, and there are 10 boys, we can use proportions to find the number of girls (20).
Beyond the Numbers: Context and Interpretation
It's crucial to understand that the numerical value alone (1/6, 0.1667, or 16.67%) doesn't tell the whole story. The context is vital for proper interpretation. For example, a 16.67% defect rate in manufacturing might be disastrous, while a 16.67% success rate in a highly risky venture could be considered a significant achievement. Always consider the specific circumstances when analyzing data.
Common Misconceptions and Clarifications
Several misconceptions often arise when dealing with proportions:
-
Ignoring Simplification: Failing to simplify the fraction 40/240 to 1/6 can lead to unnecessary complexity in calculations and interpretations.
-
Misinterpreting Percentages: Confusing 16.67% with a significantly higher or lower value due to a lack of understanding of the context.
-
Incorrect Application of Proportions: Mistakingly applying proportional reasoning in situations where it doesn't apply, leading to incorrect conclusions.
Frequently Asked Questions (FAQ)
Q1: How can I calculate the percentage of 40 out of 240 quickly?
A1: The quickest method involves simplifying the fraction first (40/240 = 1/6) and then multiplying the simplified fraction by 100: (1/6) * 100 ≈ 16.67%.
Q2: What if the numbers aren't whole numbers?
A2: The same principles apply. You'll still represent the numbers as a fraction, simplify it if possible, and then convert to a decimal or percentage as needed.
Q3: Are there any online calculators to help with this?
A3: While many online calculators can compute percentages, understanding the underlying mathematical principles is more valuable in the long run. These calculators can be used for verification, but not as a replacement for understanding the process.
Q4: How can I improve my understanding of ratios and proportions?
A4: Practice is key! Work through various examples involving ratios and proportions from different fields. Start with simpler problems and gradually work your way up to more complex scenarios. Consider using online resources or textbooks to enhance your understanding.
Conclusion: Mastering the Fundamentals
Understanding "40 out of 240" extends beyond simply calculating a fraction, decimal, or percentage. It's about grasping the fundamental concepts of ratios, proportions, and their significance in various applications. By mastering these principles, you'll enhance your ability to analyze data, solve problems, and interpret information in a more informed and efficient manner. This skill is invaluable across numerous disciplines, from finance and statistics to science and everyday life. Remember to always consider the context and avoid common misconceptions to ensure accurate and meaningful interpretations. The ability to understand and apply these concepts is a cornerstone of mathematical literacy and a vital skill for success in many areas. Continue practicing, exploring different examples, and expanding your knowledge to truly master this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Mariana Trench Pictures
Sep 12, 2025
-
Red Dress Red
Sep 12, 2025
-
50 2kg In Stone
Sep 12, 2025
-
320 Km Miles
Sep 12, 2025
-
700 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.