40 Of 160
stanleys
Sep 10, 2025 · 7 min read
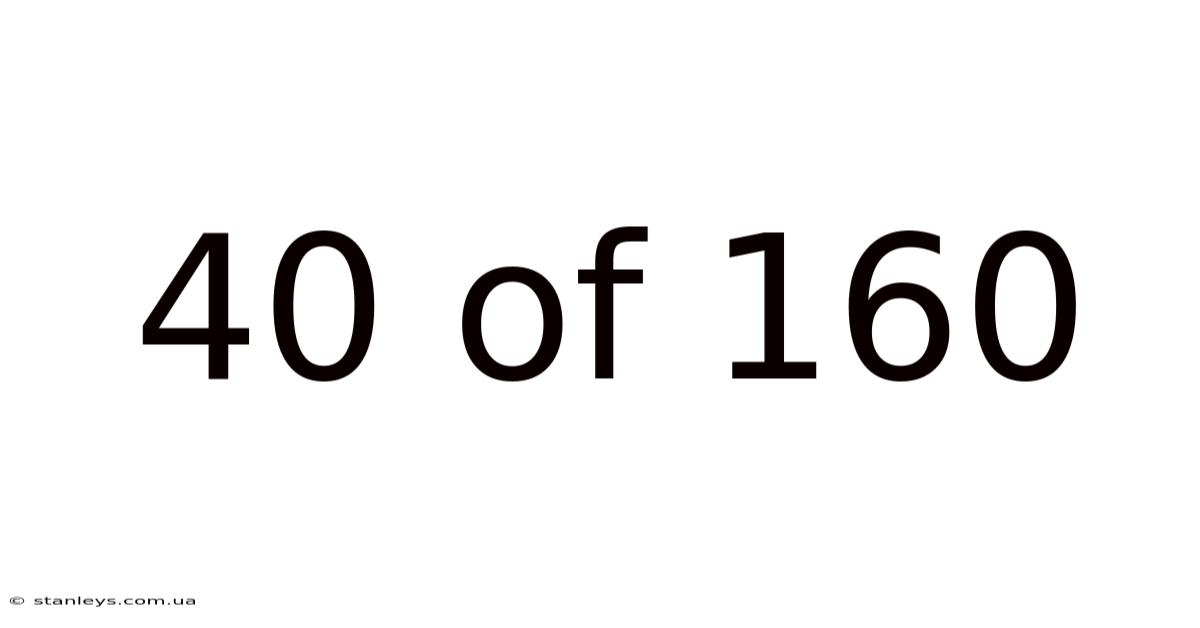
Table of Contents
Decoding the Enigma: Understanding the Ratio 40:160 and its Implications
The ratio 40:160, while seemingly simple at first glance, opens a door to a world of mathematical concepts and practical applications across various fields. This article delves deep into the meaning, simplification, applications, and implications of this ratio, exploring its presence in different contexts and clarifying common misconceptions. Understanding this ratio allows us to appreciate the fundamental principles of mathematics and their relevance in our daily lives.
Introduction: Simplifying Fractions and Ratios
At its core, 40:160 represents a ratio, a comparison of two numbers showing their relative sizes. It can also be expressed as a fraction, 40/160. Before exploring its implications, it's crucial to simplify this fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both numbers and dividing both the numerator and the denominator by it.
The GCD of 40 and 160 is 40. Dividing both numbers by 40, we get:
40 ÷ 40 = 1 160 ÷ 40 = 4
Therefore, the simplified ratio is 1:4 or the fraction 1/4. This simplified form makes it easier to understand and apply the ratio in various contexts. This fundamental simplification highlights the importance of reducing fractions to their simplest form for clearer understanding and efficient calculations.
Applications in Real-World Scenarios
The 1:4 ratio, derived from 40:160, finds its application in numerous real-world scenarios, spanning various fields:
-
Cooking and Baking: Recipes often use ratios to maintain consistency and flavor. A recipe calling for a 1:4 ratio of sugar to flour means that for every one unit of sugar, you'll use four units of flour. This could translate to 1 cup of sugar and 4 cups of flour, or 1 tablespoon of sugar and 4 tablespoons of flour. The original ratio 40:160 could represent a larger batch of the same recipe.
-
Scale Models and Drawings: Architects and engineers use ratios to represent large structures in smaller, manageable models or drawings. A 1:4 scale means that 1 unit on the model represents 4 units in reality. This allows for detailed planning and visualization before actual construction. The 40:160 ratio might represent a specific measurement on a larger blueprint scaled down for easier handling.
-
Mixing Solutions: In chemistry and other sciences, precise ratios are crucial when mixing solutions. A 1:4 ratio of solute to solvent ensures a specific concentration. This precise mixing is essential for accurate experimental results and reproducible outcomes. The larger ratio 40:160 could represent a larger volume of the same solution.
-
Financial Ratios: In finance, ratios are used to analyze the financial health of a company. Profit margins, debt-to-equity ratios, and liquidity ratios are all expressed as ratios. While 40:160 might not directly represent a specific financial ratio, understanding ratio analysis is crucial for making sound financial decisions. The simplified 1:4 ratio could represent a simplified representation of a more complex financial indicator.
-
Geometry and Proportions: The 1:4 ratio is directly applicable in geometry, especially when dealing with similar shapes. If two similar shapes have corresponding sides in a 1:4 ratio, then their areas will be in a 1:16 ratio, and their volumes in a 1:64 ratio. This understanding is crucial in scaling drawings, calculating areas, and volumes. The original ratio, 40:160, could describe the relationship between corresponding sides of two similar geometric figures.
Percentage Equivalence
Expressing the ratio 1:4 as a percentage provides another useful perspective. To do this, we can convert the fraction 1/4 into a percentage by multiplying it by 100:
(1/4) * 100 = 25%
This means that the ratio 40:160 is equivalent to 25%. This percentage representation is valuable for quick comparisons and interpretations in various contexts, especially when dealing with proportions and probabilities.
Understanding Proportions and Direct Proportionality
The ratio 40:160, simplified to 1:4, demonstrates the concept of direct proportionality. This means that as one quantity increases, the other quantity increases proportionally. For example, if you increase the amount of sugar in a recipe (maintaining the 1:4 ratio), the amount of flour must also increase proportionally to maintain the recipe's balance. This direct relationship is fundamental in many scientific and mathematical applications.
Inverse Proportionality: A Contrasting Concept
While the 40:160 ratio exemplifies direct proportionality, it's important to understand the contrasting concept of inverse proportionality. In inverse proportionality, as one quantity increases, the other quantity decreases proportionally. For instance, the relationship between speed and time taken to cover a fixed distance is inversely proportional. Understanding both direct and inverse proportionality is essential for tackling a wide range of mathematical and real-world problems.
Visual Representation and Graphical Interpretation
Visualizing the ratio 40:160 (or its simplified form 1:4) using graphs or diagrams can significantly aid understanding. A simple bar graph comparing the two numbers, or a pie chart representing the proportion of each part, can provide a clear and intuitive visual representation. This visual representation can improve understanding and communication, particularly when explaining complex concepts to diverse audiences. For example, a pie chart would show a 25% segment representing the smaller quantity and a 75% segment representing the larger quantity.
Advanced Applications: Statistical Analysis and Probability
While seemingly basic, the ratio 40:160 (1:4) has implications in more advanced areas like statistical analysis and probability. For example, if a certain event has a probability of 1/4 (or 25%), understanding this ratio helps in calculating the likelihood of that event occurring multiple times or within a specific timeframe. This has implications in various fields, including risk assessment, financial modeling, and quality control.
Addressing Common Misconceptions
A common misconception is that ratios are only relevant in specific fields like mathematics or engineering. However, ratios are implicitly or explicitly used in many aspects of daily life, from cooking and shopping to budgeting and decision-making. Understanding ratios empowers informed decision-making in various contexts.
Another misconception is that simplifying ratios is unnecessary. While the original ratio 40:160 conveys the same information as 1:4, simplifying to the lowest terms makes calculations easier, interpretation clearer, and communication more efficient. This simplified form is crucial for effective problem-solving and streamlined analysis.
Frequently Asked Questions (FAQ)
-
Q: Can I use different units for the numbers in the ratio? A: Yes, as long as the units are consistent within the ratio. For example, you could have a ratio of 40 centimeters to 160 centimeters, or 40 grams to 160 grams. The simplified ratio would remain 1:4.
-
Q: What if the numbers in the ratio are not whole numbers? A: The same principles apply. Simplify the ratio by dividing both numbers by their GCD, even if the resulting numbers are decimals or fractions.
-
Q: How can I use this ratio to solve problems? A: Use the simplified ratio (1:4) to set up a proportion. For example, if you know one quantity, you can use the ratio to find the corresponding value of the other quantity.
-
Q: Are there any online tools to simplify ratios? A: Yes, many online calculators and math tools can quickly simplify ratios and fractions.
Conclusion: The Power of Simple Ratios
The seemingly simple ratio 40:160, simplified to 1:4, reveals a wealth of mathematical concepts and practical applications. Understanding this ratio and its simplified form provides a foundation for comprehending proportions, direct and inverse proportionality, percentage calculations, and advanced applications in various fields. By mastering the basic principles of ratio simplification and analysis, we can enhance our problem-solving skills and make informed decisions in numerous aspects of our lives. This seemingly basic concept, when fully understood, unlocks a powerful tool for navigating the world around us. The journey from 40:160 to 1:4 is not just about simplifying numbers; it's about simplifying understanding and empowering practical application.
Latest Posts
Latest Posts
-
Erasmus Darwin Academy
Sep 10, 2025
-
Non Participatory Observation
Sep 10, 2025
-
135lb To Kg
Sep 10, 2025
-
Chia Seeds Punjabi
Sep 10, 2025
-
93kg To Stone
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.