40 Of 14
stanleys
Sep 12, 2025 · 5 min read
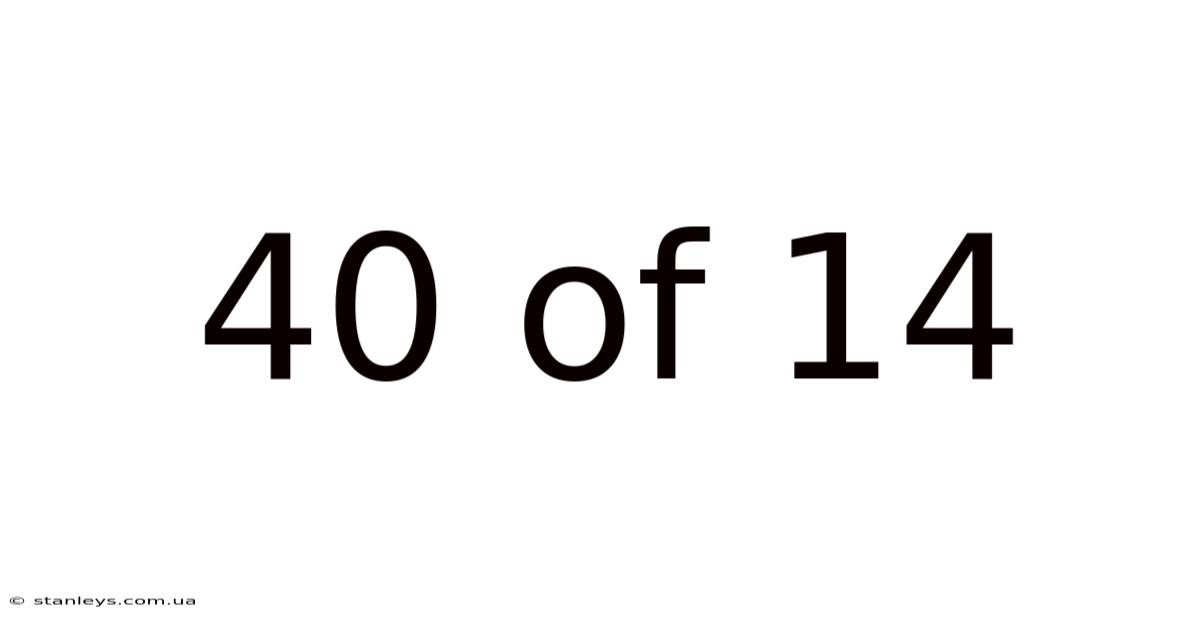
Table of Contents
Decoding the Enigma: Understanding the Fraction 40/14
The seemingly simple fraction 40/14 might appear innocuous at first glance. However, beneath its unassuming surface lies a world of mathematical concepts, from basic simplification to deeper explorations of rational numbers and their applications. This article will delve into the multifaceted nature of 40/14, exploring its simplification, decimal representation, applications, and related mathematical ideas. We’ll also address frequently asked questions to ensure a comprehensive understanding of this seemingly simple fraction.
I. Simplifying 40/14: Finding the Greatest Common Divisor (GCD)
The first step in working with any fraction is simplification. This involves reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator (40) and the denominator (14). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 40 and 14, we can use several methods. One common method is the Euclidean algorithm:
- Divide the larger number (40) by the smaller number (14): 40 ÷ 14 = 2 with a remainder of 12.
- Replace the larger number with the smaller number (14) and the smaller number with the remainder (12): Now we find the GCD of 14 and 12.
- Repeat the process: 14 ÷ 12 = 1 with a remainder of 2.
- Continue until the remainder is 0: 12 ÷ 2 = 6 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Alternatively, we can find the prime factorization of both numbers:
- 40 = 2³ x 5
- 14 = 2 x 7
The common factor is 2, therefore the GCD is 2.
Now, we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
40/14 = (40 ÷ 2) / (14 ÷ 2) = 20/7
Therefore, the simplified form of 40/14 is 20/7.
II. Decimal Representation and Mixed Numbers
While 20/7 is the simplified fractional form, it's often useful to represent the fraction as a decimal or a mixed number.
To convert 20/7 to a decimal, we perform the division: 20 ÷ 7 ≈ 2.857142857...
This is a repeating decimal, indicated by the repeating sequence "857142". We can represent this using a bar over the repeating digits: 2.$\overline{857142}$.
To express 20/7 as a mixed number, we perform the division and express the remainder as a fraction:
20 ÷ 7 = 2 with a remainder of 6.
So, 20/7 can be written as the mixed number 2 6/7.
III. Applications of 40/14 and Related Fractions
Fractions like 40/14 appear frequently in various contexts, including:
-
Real-world problems: Imagine you have 40 apples and want to divide them equally among 14 friends. The fraction 40/14 represents the number of apples each friend receives (20/7 or approximately 2.86 apples). This showcases the practical application of fractions in everyday scenarios involving sharing and division.
-
Measurement and scaling: In engineering, construction, or cooking, fractions are used for precise measurements. 40/14 might represent a ratio of two lengths or quantities in a design or recipe.
-
Probability and statistics: Fractions are fundamental in probability calculations. If an event has a probability of 40/14 (simplified to 20/7), this means the event is more likely to occur than not.
-
Algebra and equation solving: Fractions are essential building blocks in algebraic expressions and equations. Understanding fractions is vital for solving various types of equations.
IV. Exploring Further Mathematical Concepts
The fraction 40/14 provides an excellent starting point for exploring several key mathematical concepts:
-
Rational Numbers: The fraction 40/14 is a rational number, meaning it can be expressed as the quotient of two integers. Understanding rational numbers is crucial for advanced mathematical studies.
-
Equivalent Fractions: 40/14, 20/7, and other fractions that simplify to 20/7 are all equivalent fractions – they represent the same value.
-
Improper Fractions and Mixed Numbers: 20/7 is an improper fraction (the numerator is greater than the denominator), while 2 6/7 is a mixed number (a whole number and a proper fraction). Knowing how to convert between these forms is important.
-
Decimal Expansions: The decimal expansion of 20/7 illustrates the concept of repeating decimals, a crucial aspect of number theory.
-
Continued Fractions: The fraction 20/7 can also be represented as a continued fraction, a unique and powerful way to represent rational and irrational numbers.
V. Frequently Asked Questions (FAQ)
Q1: Is 40/14 a proper or improper fraction?
A1: 40/14 is an improper fraction because the numerator (40) is greater than the denominator (14).
Q2: How do I convert 40/14 to a percentage?
A2: First, simplify the fraction to 20/7. Then, divide 20 by 7 to get the decimal equivalent (approximately 2.857). Multiply by 100 to convert to a percentage: 2.857 x 100 ≈ 285.7%.
Q3: What are some real-world examples where I might encounter a fraction like 40/14?
A3: Imagine dividing 40 liters of paint equally among 14 rooms, or sharing 40 cookies among 14 friends. These situations illustrate how fractions can represent the division of quantities into equal parts.
Q4: How can I determine if two fractions are equivalent?
A4: Simplify both fractions to their lowest terms. If both simplified fractions are identical, then they are equivalent. For example, 40/14 and 20/7 are equivalent because they both simplify to 20/7.
Q5: What is the significance of the greatest common divisor (GCD) in simplifying fractions?
A5: The GCD helps us find the simplest form of a fraction. Dividing both the numerator and denominator by their GCD reduces the fraction to its lowest terms without changing its value. This simplification makes the fraction easier to work with and understand.
VI. Conclusion
The fraction 40/14, though seemingly simple, reveals a rich tapestry of mathematical concepts. From its simplification to its decimal representation and various applications, it serves as a powerful tool for illustrating fundamental principles in arithmetic and algebra. Understanding fractions like 40/14 is not just about performing calculations; it's about grasping the underlying mathematical structures and their relevance in various real-world contexts. This knowledge forms a solid foundation for more advanced mathematical explorations. By mastering these basic concepts, you unlock a deeper understanding of the mathematical world around us. The journey of understanding 40/14, therefore, extends far beyond a simple arithmetic exercise – it’s a gateway to a deeper appreciation of numbers and their relationships.
Latest Posts
Latest Posts
-
Credit Investigation Department
Sep 12, 2025
-
32km In Miles
Sep 12, 2025
-
Victorian Era Cosmetics
Sep 12, 2025
-
Anti Bumping Granules
Sep 12, 2025
-
Cool Runnings Quotes
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.