4 X 0.4
stanleys
Sep 17, 2025 · 5 min read
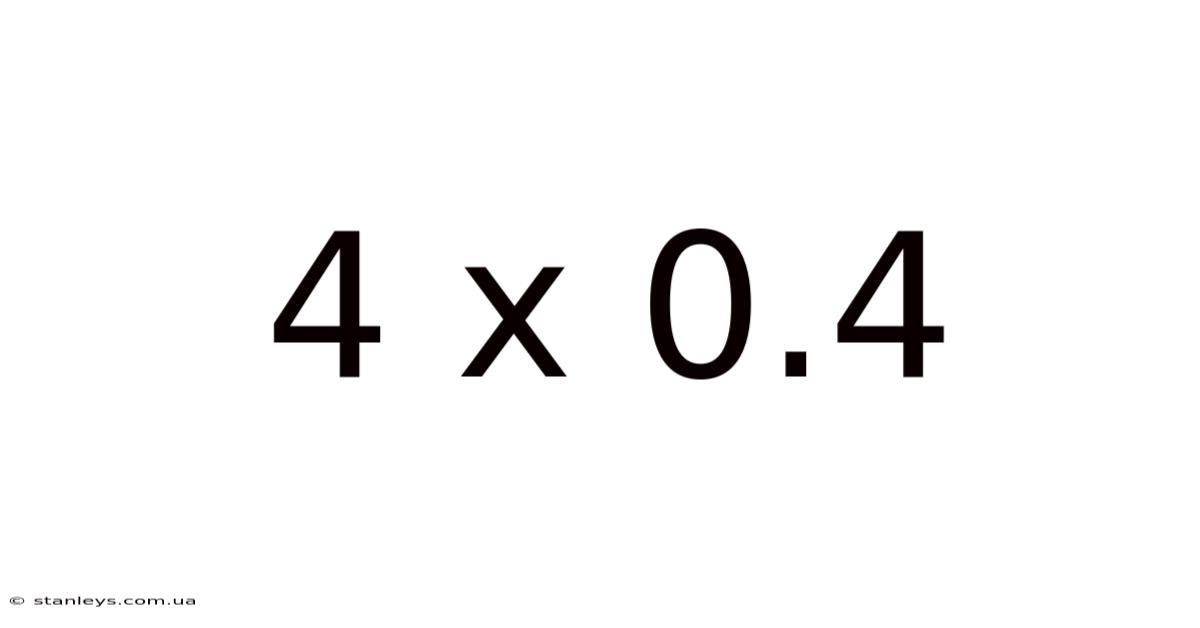
Table of Contents
Decoding 4 x 0.4: A Deep Dive into Multiplication and Decimal Numbers
This article explores the seemingly simple calculation of 4 x 0.4, delving far beyond the immediate answer to illuminate the underlying principles of multiplication, decimal numbers, and their practical applications. We'll uncover the various methods for solving this equation, discuss the theoretical underpinnings, and explore real-world scenarios where this type of calculation proves crucial. Understanding 4 x 0.4 isn't just about getting the right answer; it's about building a solid foundation in mathematics.
Understanding the Basics: Multiplication and Decimal Numbers
Before tackling 4 x 0.4, let's refresh our understanding of the core concepts involved: multiplication and decimal numbers.
Multiplication, at its heart, is repeated addition. When we say 4 x 0.4, we're essentially saying "add 0.4 to itself four times." This understanding forms the basis of several methods for solving the equation.
Decimal numbers represent parts of a whole. The number 0.4 signifies four-tenths (4/10) of a whole unit. Understanding place value is crucial here. The digit to the right of the decimal point represents tenths, the next digit represents hundredths, and so on.
Method 1: Repeated Addition
The most straightforward approach to solving 4 x 0.4 is through repeated addition:
0.4 + 0.4 + 0.4 + 0.4 = 1.6
This method visually demonstrates the concept of multiplication as repeated addition and is particularly helpful for beginners grasping the fundamental principles.
Method 2: Fraction Conversion
Decimal numbers can be easily converted into fractions, providing an alternative approach to the calculation. 0.4 is equivalent to 4/10. Therefore, 4 x 0.4 becomes:
4 x (4/10) = 16/10
Simplifying the fraction, we get:
16/10 = 8/5 = 1 3/5
Converting this improper fraction back to a decimal, we arrive at 1.6. This method reinforces the relationship between fractions and decimals.
Method 3: Standard Multiplication Algorithm
The standard multiplication algorithm, often taught in schools, provides a more efficient method for multiplying numbers, especially with larger values. While seemingly complex for this specific problem, understanding this method is crucial for tackling more intricate calculations.
To use this method, we ignore the decimal point initially and multiply 4 by 4, resulting in 16. Then, we count the total number of decimal places in the original numbers (one decimal place in 0.4). We place the decimal point in the result, 16, one place from the right, yielding 1.6.
4 x 0.4
1.6
Method 4: Distributive Property
The distributive property of multiplication allows us to break down complex calculations into simpler ones. While not strictly necessary for 4 x 0.4, it's a valuable tool for understanding more complex multiplication problems. We can rewrite 0.4 as (0.1 x 4). The calculation then becomes:
4 x (0.1 x 4) = (4 x 0.1) x 4 = 0.4 x 4 = 1.6
Real-World Applications: Where 4 x 0.4 Matters
The seemingly simple equation 4 x 0.4 has surprisingly wide-ranging applications in various fields:
- Finance: Calculating discounts, interest, or portions of a budget. For example, a 40% discount (0.4) on a $4 item.
- Engineering: Scaling down dimensions or calculating material quantities. Reducing a 4-meter length by 40%.
- Cooking and Baking: Adjusting recipes, scaling ingredients up or down proportionally. Using 40% of a 4-cup ingredient.
- Science: Determining proportions in experiments, calculating concentrations, or scaling down models. Mixing 40% of a 4-liter solution.
- Everyday Life: Calculating the cost of multiple items, splitting bills evenly, or determining distances.
Beyond the Basics: Exploring Decimal Multiplication in Depth
The calculation 4 x 0.4 provides a gateway to a deeper understanding of decimal multiplication. Let's delve into some key aspects:
- Place Value: Understanding place value is fundamental to working with decimals. Each digit holds a specific value based on its position relative to the decimal point.
- Estimation: Before performing a calculation, estimating the answer helps to verify the reasonableness of the result. In this case, we know the answer should be slightly less than 4 (since we're multiplying by a number less than 1).
- Significant Figures: In scientific and engineering contexts, significant figures determine the precision of a measurement. The number of significant figures in the result depends on the precision of the input values.
- Rounding: When dealing with decimal numbers, rounding to a specific number of decimal places is often necessary to simplify the result or reflect the accuracy of the measurement.
Frequently Asked Questions (FAQ)
Q1: What if one of the numbers was a whole number and the other a decimal?
A1: The process remains the same. You can use any of the methods described above. For example, 4 x 2.5 involves multiplying 4 by 25 and then adjusting the decimal place according to the number of decimal places in the original numbers.
Q2: How would you handle larger decimal numbers?
A2: The same principles apply. Use the standard multiplication algorithm, paying close attention to the placement of the decimal point based on the total number of decimal places in the original numbers.
Q3: Are there any shortcuts for multiplying decimals?
A3: While no major shortcuts exist for all decimal multiplications, understanding the relationship between fractions and decimals can sometimes simplify calculations. Also, mastering the standard algorithm allows for efficient computation, especially with larger numbers.
Q4: What if I make a mistake?
A4: Don't worry! Mistakes are a part of learning. Review your work carefully, check each step, and try using a different method to see if you get the same result.
Conclusion: Mastering the Fundamentals
Solving 4 x 0.4 is more than just arriving at the answer 1.6. It's about grasping the fundamental principles of multiplication, decimals, and their practical applications. By exploring different methods, understanding the underlying concepts, and recognizing its relevance in various contexts, we can build a strong mathematical foundation. This seemingly simple calculation opens doors to a more profound understanding of numerical operations, empowering us to tackle more complex mathematical challenges with confidence. Remember, practice is key! The more you work with these concepts, the more intuitive and effortless they become. So keep practicing, keep exploring, and keep expanding your mathematical horizons.
Latest Posts
Latest Posts
-
Katniss Fire Dress
Sep 17, 2025
-
Face Paint Green
Sep 17, 2025
-
82 5kg In Pounds
Sep 17, 2025
-
8 Of 2500
Sep 17, 2025
-
68inches In Cm
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 X 0.4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.