4 Of 1000000
stanleys
Sep 12, 2025 · 6 min read
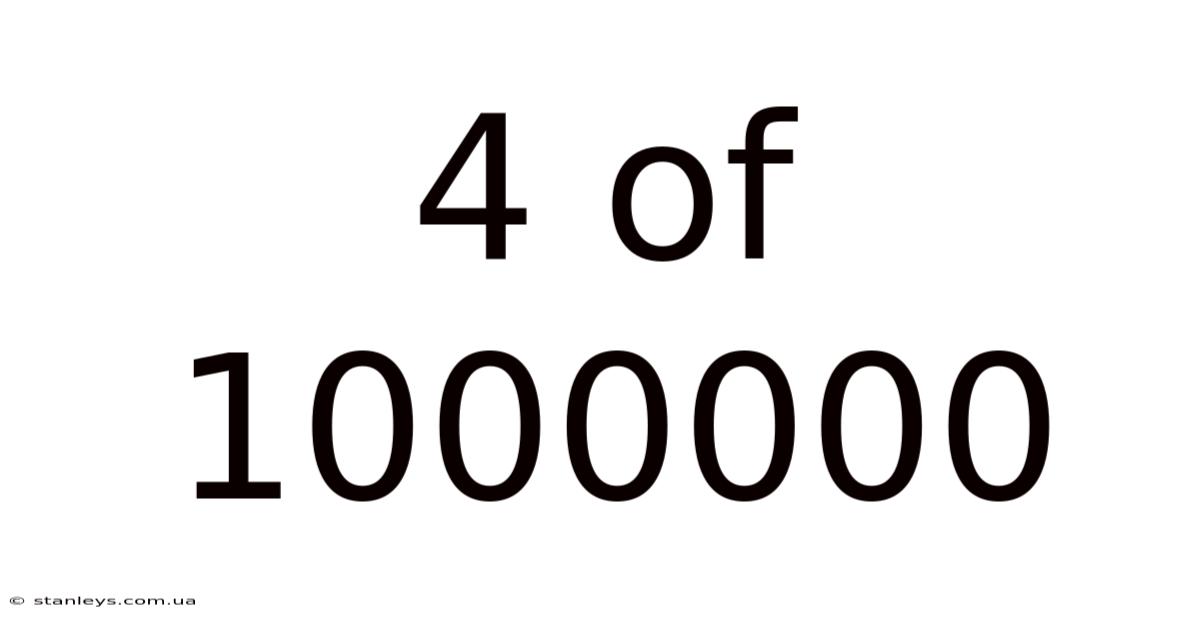
Table of Contents
Decoding the Infinitesimal: Exploring the Significance of 4 out of 1,000,000
Understanding probabilities and proportions is fundamental to many aspects of life, from everyday decision-making to complex scientific calculations. This article delves into the seemingly insignificant fraction represented by 4 out of 1,000,000, exploring its meaning, implications, and how such small probabilities impact various fields. We’ll unpack the mathematical representation, explore its relevance in different contexts, and address common misconceptions surrounding extremely low probabilities.
Understanding the Fraction: 4/1,000,000
The fraction 4/1,000,000 represents a very small proportion. To grasp its magnitude, we can express it in several ways:
- Decimal: 0.000004. This clearly shows the minuscule nature of the fraction.
- Percentage: 0.0004%. This highlights that it represents only four ten-thousandths of a percent.
- Ratio: 4:1,000,000. This emphasizes the stark difference between the numerator and denominator.
This incredibly small number might seem inconsequential at first glance. However, depending on the context, it can hold significant weight, particularly when dealing with large populations or frequent events.
Context is Key: Where 4/1,000,000 Matters
The importance of 4/1,000,000 is entirely dependent on the context in which it's applied. Let's explore a few examples:
1. Risk Assessment and Public Health:
Imagine a new drug with a side effect occurring in 4 out of 1,000,000 patients. While the probability seems minuscule, consider the global population. Even a small percentage translates to a substantial number of individuals affected. Pharmaceutical companies and regulatory bodies meticulously analyze such low probabilities to weigh the benefits of a drug against its potential risks. The calculation of risk and benefit is crucial in making informed decisions, even with extremely low probabilities. Similar considerations apply to analyzing the risk of rare diseases or the efficacy of preventative measures.
2. Lottery Probabilities:
Lottery winnings often involve extremely low probabilities. Winning the jackpot might have odds similar to 4/1,000,000 or even lower. Understanding these odds is crucial for managing expectations and responsible gambling. While the allure of a large payout is tempting, it's vital to recognize the minuscule chance of success. The vast majority of lottery participants will not win, highlighting the impracticality of relying on such low-probability events.
3. Scientific Research and Statistical Significance:
In scientific research, particularly in fields like genetics or epidemiology, researchers often deal with very large datasets and extremely low probabilities. A correlation observed with a probability as low as 4/1,000,000 might be considered statistically significant, indicating a genuine effect rather than mere chance. However, careful consideration of confounding factors and rigorous statistical analysis are crucial to avoid false conclusions. Statistical significance thresholds (p-values) are precisely designed to evaluate the reliability of observed results.
4. Manufacturing and Quality Control:
In manufacturing processes, even extremely low defect rates can have significant consequences. If a particular component in a car has a defect rate of 4/1,000,000, it might seem negligible. However, considering the millions of cars produced annually, the actual number of defective components becomes substantial. Quality control measures are implemented to detect and mitigate such defects, even at extremely low probabilities. The cost of recalling defective products or dealing with customer complaints can outweigh the cost of maintaining stricter quality control.
Mathematical Considerations and Misconceptions
Several mathematical concepts are vital to understanding probabilities like 4/1,000,000:
-
The Law of Large Numbers: This law states that the more trials or observations made, the closer the observed frequency of an event will approach its true probability. While the probability of a single event is low, repeating the event a massive number of times increases the likelihood of observing the outcome.
-
Binomial Distribution: This distribution models the probability of getting a specific number of successes (e.g., defective components) in a fixed number of independent trials. The binomial distribution is valuable in analyzing situations where success or failure probabilities are consistent.
-
Poisson Distribution: If the probability of an event is very low, and the number of trials is very large, the Poisson distribution offers a useful approximation to the binomial distribution. It simplifies calculations when dealing with extremely low probabilities.
A common misconception is that because the probability is low, the event will never happen. This is incorrect. While the likelihood is minimal, it's not impossible. The event can occur, especially if the number of opportunities for it to occur is sufficiently large.
Another misconception is that extremely low probabilities should always be dismissed as insignificant. This is not true. As we've seen, the context is crucial. In fields like public health or risk management, even small probabilities can represent significant risks when scaled to large populations or numerous trials.
Beyond the Numbers: The Human Element
While the mathematical aspects are essential, it's equally important to consider the human element. The emotional response to probabilities varies. A 4/1,000,000 chance of a serious side effect from a medication might lead to anxiety for some individuals, while others might dismiss it as inconsequential. Clear and transparent communication about probabilities is vital for informed decision-making and managing public perception. Understanding the emotional weight of such probabilities, particularly in health-related contexts, helps in crafting better communication strategies. Effective communication should avoid technical jargon and prioritize clarity and transparency.
Furthermore, the concept of perceived risk often differs from the actual statistical risk. People might overestimate the probability of certain events (like plane crashes) and underestimate others (like car accidents). Addressing these cognitive biases is essential to promote informed decision-making based on factual probabilities, rather than subjective perceptions.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate the probability of this event not happening?
- A: The probability of the event not happening is 1 - (4/1,000,000) = 999,996/1,000,000, or approximately 99.9996%.
-
Q: What if the number of trials increases significantly?
- A: As the number of trials increases, the probability of the event occurring at least once increases. While the individual probability remains low, the cumulative probability across a large number of trials becomes more significant.
-
Q: How can I apply this concept to real-life scenarios?
- A: Consider applying this to assessing risks in various contexts, such as evaluating the effectiveness of a vaccine, assessing the probability of a manufacturing defect, or analyzing the potential impact of a natural disaster in a specific location.
Conclusion: A Deeper Appreciation for the Infinitesimal
The seemingly small fraction of 4/1,000,000 might appear insignificant at first. However, upon closer inspection and within specific contexts, it reveals its importance. Understanding probabilities, particularly low-probability events, is crucial in various fields. This includes risk assessment, scientific research, quality control, and informed decision-making. This article has explored the mathematical representation, its application in different scenarios, addressed common misconceptions, and highlighted the human element involved in perceiving and interpreting such probabilities. Ultimately, comprehending and applying the concepts discussed here empowers us to make more informed decisions in a world full of uncertainties. Remember, context is paramount, and while the probability might seem minuscule, its impact can be substantial, depending on the specific situation and the scale involved.
Latest Posts
Latest Posts
-
20 Of 28
Sep 12, 2025
-
3 2 Km Miles
Sep 12, 2025
-
Mmhg En Pa
Sep 12, 2025
-
2 Of 300
Sep 12, 2025
-
10 Of 125
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 4 Of 1000000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.