35percent Of 360
stanleys
Sep 15, 2025 · 5 min read
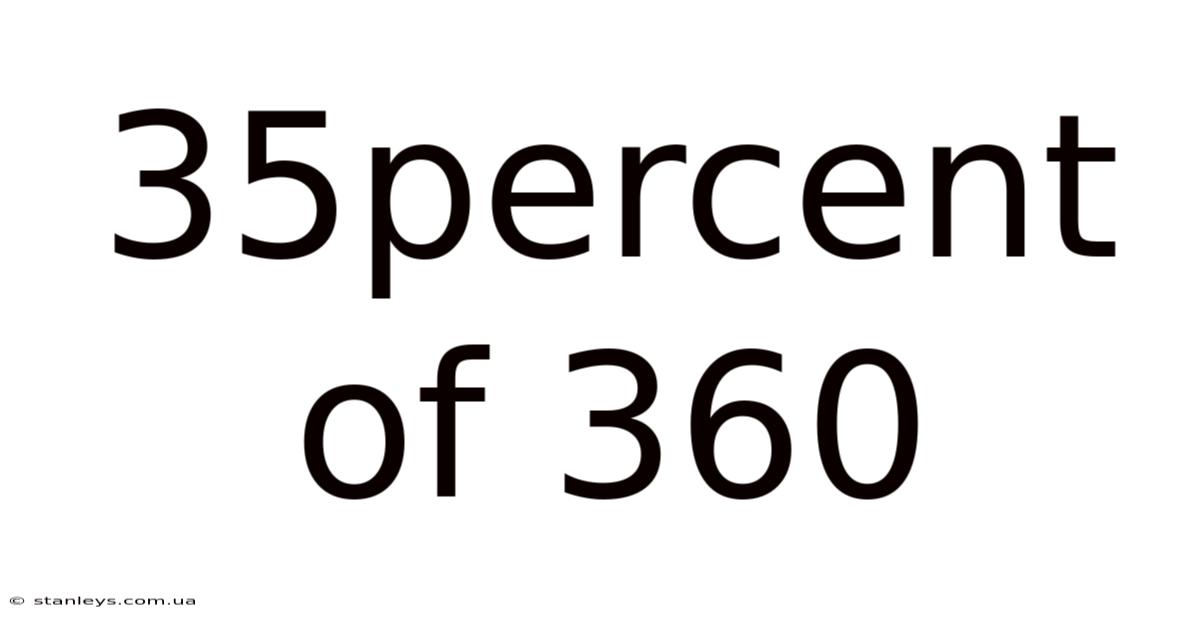
Table of Contents
Decoding 35% of 360: A Comprehensive Guide to Percentage Calculations
Finding 35% of 360 might seem like a simple task, but understanding the underlying principles of percentage calculations is crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article provides a comprehensive guide to solving this specific problem and explores the broader concept of percentages, equipping you with the skills to tackle similar calculations confidently. This guide will delve into multiple methods, from basic arithmetic to using calculators and even exploring the conceptual understanding behind percentages. Let's dive in!
Understanding Percentages: The Fundamentals
Before we tackle finding 35% of 360, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
This fundamental understanding forms the basis of all percentage calculations. We can express any percentage as a decimal or a fraction, making calculations more manageable. To convert a percentage to a decimal, simply divide the percentage by 100. For instance, 35% becomes 35/100 = 0.35. Converting to a fraction is equally straightforward; 35% is simply 35/100, which can be simplified to 7/20.
Method 1: Using the Basic Formula
The most straightforward method to calculate 35% of 360 is to use the fundamental percentage formula:
Percentage × Whole Number = Part
In our case:
- Percentage: 35% = 0.35 (decimal form)
- Whole Number: 360
Therefore, the calculation is:
0.35 × 360 = 126
Therefore, 35% of 360 is 126.
This method is ideal for simple calculations and provides a clear understanding of the underlying mathematical process. It's the foundational method that underpins all other percentage calculation strategies.
Method 2: Fraction Method
As mentioned earlier, we can express 35% as a fraction (35/100 or simplified to 7/20). This allows us to calculate 35% of 360 as follows:
(7/20) × 360
This simplifies to:
7 × (360/20) = 7 × 18 = 126
Again, we arrive at the same answer: 35% of 360 is 126. This method is beneficial for understanding the relationship between fractions and percentages and can be particularly useful when dealing with percentages that have easy fraction equivalents.
Method 3: Using a Calculator
Modern calculators make percentage calculations incredibly simple. Most calculators have a "%" button. The process typically involves entering the whole number (360), then pressing the multiplication button (×), entering the percentage (35), and finally pressing the "%" button. The calculator will automatically perform the calculation and display the result: 126. This method is efficient and minimizes the risk of manual calculation errors, especially for more complex percentage problems.
Method 4: Breaking Down the Percentage
For a deeper understanding, we can break down the 35% into smaller, easier-to-manage percentages. For example:
- 10% of 360: 360/10 = 36
- 5% of 360: 36/2 = 18
- 30% of 360: 36 × 3 = 108
Adding these together (36 + 18 + 108) equals 162, which isn't the right answer. The error shows how we can't necessarily break down percentages additively.
Let's try a slightly different approach which is adding 10% three times and then adding 5%:
- 10% of 360 = 36
- 30% of 360 = 36 * 3 = 108
- 5% of 360 = 36 / 2 = 18
Adding these together (108 + 18) does indeed give 126. This method allows us to visualize the percentage as the sum of its components. This approach is excellent for mental math estimations and building intuition.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
- Sales and Discounts: Calculating discounts in shops, online sales, and clearance sales. If an item is 35% off, this method helps determine the final price.
- Taxes: Calculating sales tax, income tax, or other forms of taxation. Understanding tax percentages helps budget and manage personal finances.
- Financial Investments: Calculating returns on investments, interest rates, and growth percentages.
- Statistics and Data Analysis: Interpreting data presented as percentages, such as survey results, market share, and growth rates. This allows for making informed decisions.
- Science and Engineering: Calculating percentages in various scientific experiments, chemical reactions, and engineering designs.
- Cooking and Baking: Adjusting ingredient quantities in recipes based on percentage increases or decreases.
- Tip Calculations: Figuring out the appropriate amount to tip at restaurants and service establishments.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest way depends on the situation. For simple calculations, the basic formula (Percentage × Whole Number = Part) is straightforward. For more complex calculations or when accuracy is crucial, using a calculator is the most efficient and accurate method.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, then divide by the original value and multiply by 100. For a percentage decrease, follow the same steps, but the difference will be negative.
Q: Can I use a different formula to solve 35% of 360?
A: Yes, you can use the fraction method (explained earlier) or you could use a proportion: 35/100 = x/360, and solve for x. All these methods arrive at the same answer.
Q: Why is understanding percentages important?
A: Percentages are a fundamental part of everyday life, allowing us to understand proportions, make comparisons, and interpret data efficiently. This is crucial for personal finance, data interpretation and decision-making.
Q: Are there online tools to help calculate percentages?
A: Yes, many online calculators and websites are dedicated to percentage calculations. These can be helpful for double-checking manual calculations or for more complex percentage problems.
Conclusion
Calculating 35% of 360, resulting in 126, is a relatively simple percentage problem. However, understanding the underlying principles and various methods allows for a broader understanding of percentage calculations, equipping you to handle various challenges in diverse areas. Whether using the basic formula, the fraction method, a calculator, or breaking down the percentage, mastering these techniques empowers you to confidently approach and solve percentage problems in everyday life and professional endeavors. The ability to understand and manipulate percentages is a valuable skill that transcends specific calculations and becomes a cornerstone for better decision-making and comprehension of numerical information.
Latest Posts
Latest Posts
-
78f To C
Sep 15, 2025
-
5 Of 190
Sep 15, 2025
-
5 Of 1000000
Sep 15, 2025
-
Kinetic Energy Calculator
Sep 15, 2025
-
Half Of 55
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 35percent Of 360 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.