34 X 12
stanleys
Sep 13, 2025 · 6 min read
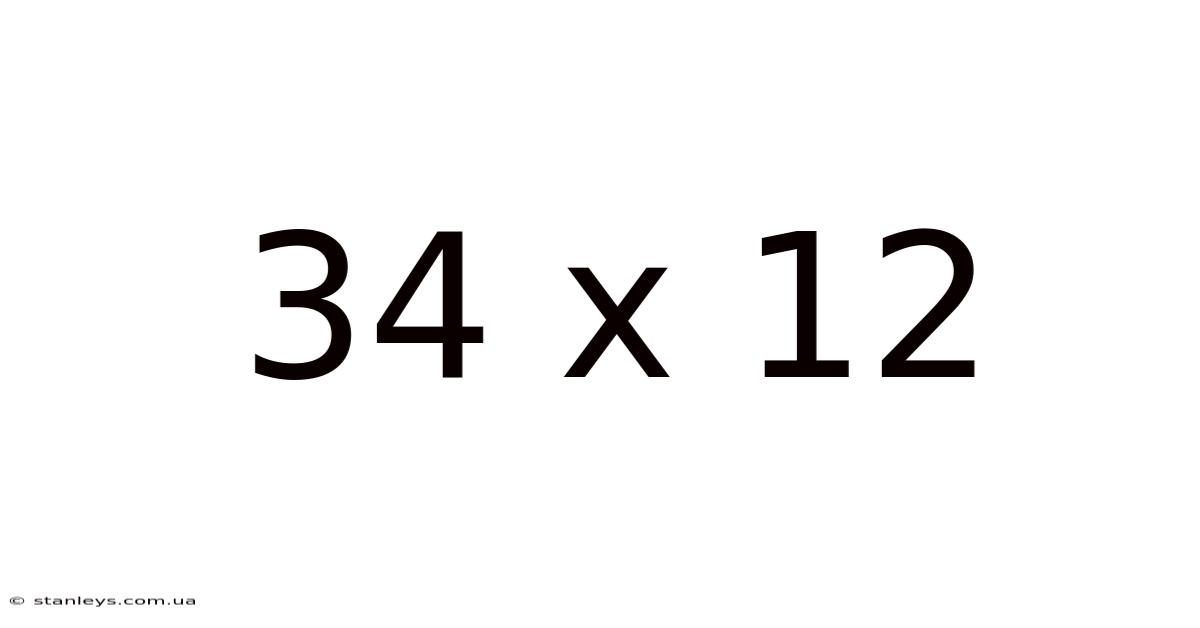
Table of Contents
Decoding 34 x 12: A Deep Dive into Multiplication and Beyond
The seemingly simple calculation of 34 x 12 might appear trivial at first glance. However, this seemingly basic arithmetic problem opens a door to exploring various mathematical concepts, from fundamental multiplication strategies to more advanced applications in algebra and beyond. This article will delve into the multiple ways to solve 34 x 12, explaining the underlying principles and showcasing the practical relevance of this calculation in everyday life and higher-level mathematics. We'll cover different methods, explore the underlying logic, and even touch upon real-world applications to demonstrate the far-reaching implications of this simple equation.
Understanding the Basics: Multiplication Fundamentals
Before diving into the different methods of solving 34 x 12, let's establish a firm grasp on the fundamental principles of multiplication. Multiplication is essentially repeated addition. In the case of 34 x 12, we're essentially adding 34 twelve times: 34 + 34 + 34 + 34 + 34 + 34 + 34 + 34 + 34 + 34 + 34 + 34. While this method is conceptually straightforward, it's incredibly time-consuming for larger numbers. That's where the power of multiplication algorithms comes into play.
Method 1: Standard Multiplication Algorithm
The standard multiplication algorithm, taught in most elementary schools, involves breaking down the multiplication into smaller, manageable steps. Let's apply this method to 34 x 12:
34
x 12
------
68 (34 x 2)
+340 (34 x 10)
------
408
This method involves multiplying 34 by each digit of 12 separately (2 and 10) and then adding the results. The placement of the zero in 340 is crucial, signifying the multiplication by 10. This systematic approach ensures accuracy and efficiency, particularly for larger numbers. Understanding the place value system (ones, tens, hundreds, etc.) is fundamental to mastering this algorithm.
Method 2: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can apply this to solve 34 x 12 by breaking down 12 into 10 + 2:
34 x 12 = 34 x (10 + 2) = (34 x 10) + (34 x 2) = 340 + 68 = 408
This method offers a more conceptual understanding of the multiplication process, highlighting the underlying mathematical principles. It's an excellent approach for building a solid foundation in algebra, where the distributive property is widely used.
Method 3: Lattice Multiplication
Lattice multiplication, a visually appealing and less prone-to-error method, provides an alternative approach. It involves creating a grid and breaking down the numbers:
3 | 4
-----+-----
1 | 3 | 4
1 | 0 | 0
-----+-----
| 6 | 8
+3 | 4 | 0
-----+-----
4 | 0 | 8
Each cell represents the product of the digits above and to the left. Adding along the diagonals gives the final result (408). This method can be particularly helpful for visualizing the multiplication process and simplifying calculations with larger numbers.
Method 4: Mental Math Techniques
Mastering mental math involves developing strategies for quick calculations without relying on pen and paper. For 34 x 12, one approach involves doubling and halving:
- Double 34 to get 68.
- Halve 12 to get 6.
- Multiply 68 x 6: (60 x 6) + (8 x 6) = 360 + 48 = 408
This technique requires familiarity with multiplication tables and the ability to perform quick mental calculations. Practice and understanding number relationships are key to developing proficiency in mental math.
The Significance of Place Value in Multiplication
The correct placement of digits is paramount in multiplication. Understanding the concept of place value—ones, tens, hundreds, thousands, etc.—is crucial for performing accurate calculations. Errors often arise from incorrect positioning of digits, leading to incorrect answers. The zero placeholder in the standard algorithm (340) is a critical element illustrating the multiplication by 10. Ignoring place value renders the calculation meaningless.
Applications of 34 x 12 in Real-World Scenarios
While seemingly abstract, the calculation of 34 x 12 has practical applications in various contexts:
- Calculating Costs: Imagine you're buying 34 items priced at $12 each. The total cost is 34 x 12 = $408.
- Area Calculations: If you have a rectangular area measuring 34 units by 12 units, its total area is 34 x 12 = 408 square units.
- Inventory Management: A warehouse manager calculating the total number of items in 34 boxes, each containing 12 items, uses this calculation.
These examples illustrate the practical relevance of multiplication in everyday situations. Understanding these basic calculations is fundamental for problem-solving in various fields.
Extending the Concept: Algebraic Applications
The principles underlying 34 x 12 extend into algebraic manipulations. For instance, the distributive property is a cornerstone of algebraic simplification. Consider the expression:
12(x + 34)
Applying the distributive property: 12x + (12 x 34) = 12x + 408.
Understanding the multiplication of numbers like 34 and 12 is crucial for handling more complex algebraic expressions and equations.
Beyond the Numbers: Developing Mathematical Fluency
The simple equation 34 x 12 is more than just a calculation; it's a stepping stone towards developing mathematical fluency. Fluency encompasses accuracy, efficiency, and flexibility in applying mathematical concepts. Mastering various multiplication methods and understanding the underlying principles equips you with the skills to solve more complex problems effectively.
Frequently Asked Questions (FAQ)
Q1: What is the quickest way to solve 34 x 12?
A1: The quickest method depends on individual preferences and skillsets. For some, the standard algorithm might be fastest. Others might find mental math techniques more efficient. The distributive property also provides a relatively fast approach.
Q2: Why is it important to learn different multiplication methods?
A2: Learning multiple methods enhances mathematical understanding and flexibility. Different methods appeal to diverse learning styles and provide alternative approaches to problem-solving.
Q3: How can I improve my multiplication skills?
A3: Consistent practice is key. Regularly working with multiplication problems of varying complexity helps build proficiency and automaticity. Focus on understanding the underlying principles rather than rote memorization.
Q4: Are there any online resources to help with multiplication practice?
A4: While I cannot provide external links, many educational websites and apps offer interactive multiplication practice exercises catering to various age groups and skill levels. A simple web search will yield numerous options.
Conclusion: The Enduring Power of a Simple Calculation
The equation 34 x 12, while appearing simple at first, provides a rich foundation for exploring various mathematical concepts. From fundamental multiplication techniques to the distributive property and its application in algebra, this calculation underscores the importance of mastering basic arithmetic operations. Developing mathematical fluency extends beyond rote memorization; it involves understanding underlying principles, applying multiple methods, and fostering a conceptual grasp of mathematical relationships. The seemingly simple calculation of 34 x 12 reveals a deeper, more significant aspect: the power of foundational mathematical knowledge in shaping broader understanding and problem-solving abilities. This understanding extends far beyond the classroom, impacting various aspects of our lives and professional endeavors. The more we explore the depths of such seemingly simple problems, the more we appreciate the beauty and elegance of mathematics.
Latest Posts
Latest Posts
-
139lbs In Kg
Sep 13, 2025
-
Nanogram To Gram
Sep 13, 2025
-
4 Of 500
Sep 13, 2025
-
Square Feet Sign
Sep 13, 2025
-
109kg To Pounds
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 34 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.