3/8 Of 40
stanleys
Sep 17, 2025 · 5 min read
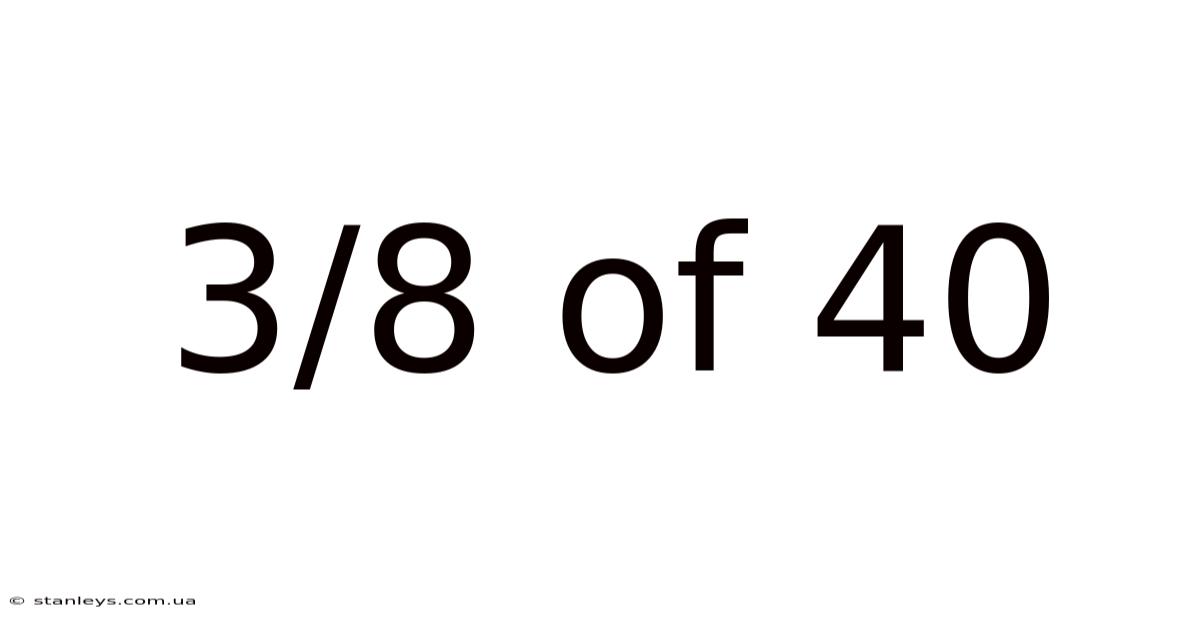
Table of Contents
Decoding 3/8 of 40: A Comprehensive Guide to Fractions and Multiplication
Understanding fractions and how to perform calculations involving them is a fundamental skill in mathematics. This comprehensive guide will delve into the seemingly simple problem of calculating "3/8 of 40," unpacking the process step-by-step and exploring the underlying mathematical concepts. We'll move beyond just finding the answer, exploring the practical applications of this type of calculation and addressing common misunderstandings surrounding fractions and multiplication. This guide aims to provide a solid foundation for anyone struggling with fractions or wanting to deepen their understanding of this crucial mathematical concept.
Understanding the Problem: 3/8 of 40
The phrase "3/8 of 40" signifies a multiplication problem involving a fraction (3/8) and a whole number (40). The word "of" in this context directly translates to multiplication. Therefore, we need to calculate (3/8) * 40. This seemingly simple problem opens the door to understanding several key mathematical concepts.
Method 1: Converting the Whole Number to a Fraction
One straightforward approach involves converting the whole number 40 into a fraction. Any whole number can be expressed as a fraction by placing it over 1. In this case, 40 becomes 40/1. Now, our problem is:
(3/8) * (40/1)
To multiply fractions, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(3 * 40) / (8 * 1) = 120 / 8
Now, we simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 8:
120 / 8 = 15
Therefore, 3/8 of 40 is 15.
Method 2: Simplifying Before Multiplying
A more efficient approach involves simplifying the fraction before performing the multiplication. We can simplify by canceling out common factors between the numerator and the denominator. Notice that 40 is divisible by 8:
(3/8) * 40 = (3/8) * (40/1)
We can simplify the fraction by dividing both 40 (in the numerator) and 8 (in the denominator) by their greatest common divisor, which is 8:
(3/1) * (5/1) = 15
This method streamlines the calculation, avoiding the need to work with larger numbers. This demonstrates the importance of simplifying fractions whenever possible to make calculations easier and less prone to errors.
Method 3: Understanding the Concept of "Of" as Multiplication
The phrase "3/8 of 40" can be interpreted as finding 3/8 of the total quantity 40. This means dividing 40 into 8 equal parts and then taking 3 of those parts.
- Divide: 40 / 8 = 5 (Each of the 8 parts is 5 units)
- Multiply: 5 * 3 = 15 (Three of these parts equal 15 units)
This approach helps visualize the problem and connects the abstract mathematical operation to a concrete representation. It's a valuable method for building intuitive understanding, especially for those new to fractions.
The Importance of Understanding Fractions
Fractions are fundamental to many aspects of life, beyond the classroom. They are crucial in:
- Cooking and Baking: Recipes often involve fractional measurements (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Construction and Engineering: Precise measurements and proportions are essential, relying heavily on fractions and decimals.
- Finance and Budgeting: Understanding percentages (which are essentially fractions) is vital for managing finances, calculating interest, and understanding discounts.
- Data Analysis: Fractions and percentages are used extensively to represent proportions and trends in data.
Mastering fractions is not just about passing math tests; it's about developing a crucial skill applicable to numerous real-world situations.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when working with fractions:
- Incorrect Multiplication: Forgetting to multiply both the numerators and the denominators. Always remember: (a/b) * (c/d) = (ac) / (bd)
- Improper Simplification: Not simplifying the fraction to its lowest terms. Always simplify to make the result easier to understand and use.
- Misunderstanding "Of": Not recognizing that "of" in this context indicates multiplication.
- Difficulty with Large Numbers: Struggling to perform the multiplication when dealing with larger numbers. Simplifying before multiplying helps to alleviate this issue.
Further Exploration: Decimals and Percentages
The result of 3/8 of 40 (which is 15) can also be expressed as a decimal (15.0) or a percentage (15/40 * 100% = 37.5%). Understanding the relationships between fractions, decimals, and percentages is crucial for a well-rounded understanding of numbers and their applications. Converting between these forms allows for flexibility in calculations and data representation.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, you can use a calculator. Simply enter (3/8) * 40. However, understanding the underlying mathematical principles is crucial for developing problem-solving skills and applying this knowledge to more complex scenarios.
Q: What if the numbers were larger or more complex?
A: The same principles apply. Always simplify fractions before multiplying, and carefully follow the steps for multiplying fractions. Breaking down complex problems into smaller, manageable steps is key to success.
Q: Are there other ways to solve this problem?
A: Yes. Other methods involve using decimals or percentages, as mentioned earlier. The best method depends on individual preference and the context of the problem.
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to many areas of life, including cooking, construction, finance, and data analysis. A strong understanding of fractions is essential for navigating many real-world situations.
Conclusion: Mastering Fractions for a Brighter Future
Calculating "3/8 of 40" might seem like a simple task, but it's a gateway to understanding fundamental mathematical concepts. By mastering the methods presented here – converting to fractions, simplifying before multiplying, and understanding the concept of "of" as multiplication – you'll gain confidence in working with fractions and applying this crucial skill to various real-world scenarios. Remember, consistent practice and a focus on understanding the underlying principles are key to mastering fractions and developing a strong foundation in mathematics. Embrace the challenge, and you'll discover the rewarding power of understanding and applying these fundamental mathematical tools. The ability to confidently tackle fraction problems is not just a mathematical achievement; it's a valuable life skill that unlocks opportunities across diverse fields and empowers you to solve complex problems with ease and precision.
Latest Posts
Latest Posts
-
25 Of 250000
Sep 17, 2025
-
1 73 In Ft
Sep 17, 2025
-
35 Of 140
Sep 17, 2025
-
15 Of 33
Sep 17, 2025
-
45 Of 400
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.