3/8 Of 24
stanleys
Sep 17, 2025 · 5 min read
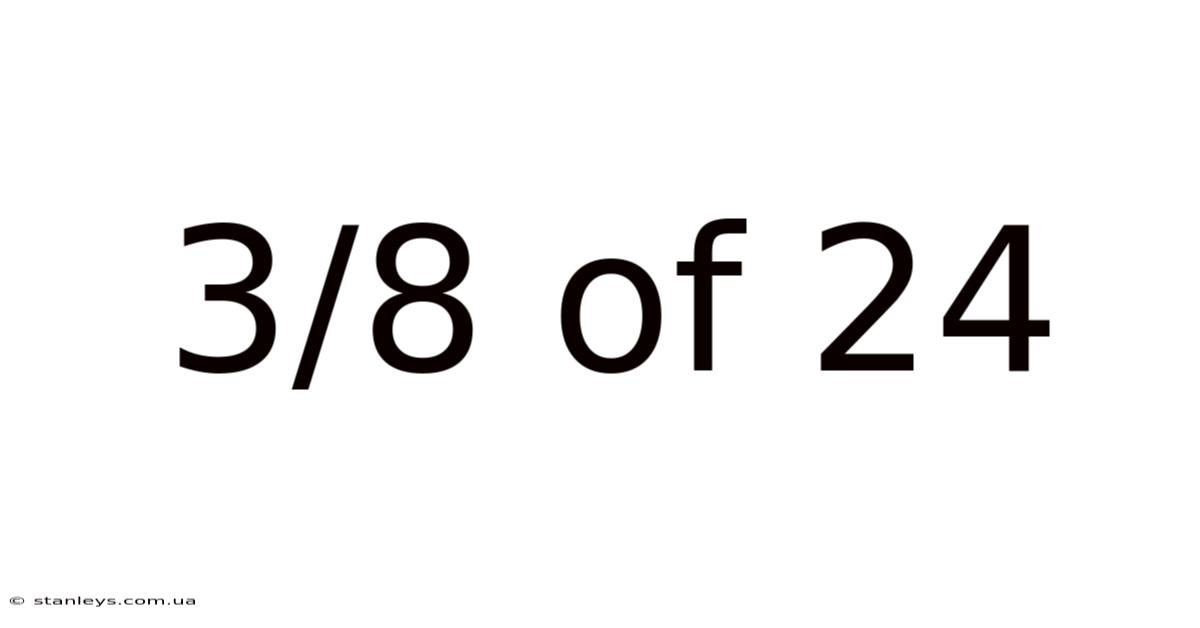
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/8 of 24
Finding 3/8 of 24 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation opens a door to understanding fundamental mathematical concepts applicable across various fields, from basic accounting to advanced calculus. This article will not only solve the problem but also explore the underlying principles, offer different approaches to solving it, and delve into the broader mathematical context. We will unravel the mystery of fractions, delve into the concept of "of" as multiplication, and even touch upon the historical significance of fractional arithmetic.
Understanding Fractions: The Building Blocks
Before we tackle 3/8 of 24, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering. In our problem, 3/8 represents three out of eight equal parts.
Understanding fractions is crucial in various real-world scenarios. Imagine sharing a pizza: if you cut it into 8 slices and you eat 3, you've consumed 3/8 of the pizza. This simple example highlights the practical application of fractions in everyday life.
"Of" Means Multiplication: The Key to the Solution
The word "of" in mathematical expressions, particularly when dealing with fractions and percentages, signifies multiplication. Therefore, "3/8 of 24" is mathematically equivalent to (3/8) * 24. This seemingly small realization is the key to unlocking the solution.
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the fraction by the whole number:
(3/8) * 24 = (3 * 24) / 8
First, we multiply the numerator (3) by the whole number (24): 3 * 24 = 72
Then, we divide the result by the denominator (8): 72 / 8 = 9
Therefore, 3/8 of 24 is 9.
Method 2: Simplifying Before Multiplication
We can simplify the calculation by reducing the fraction before multiplication. Notice that 24 is divisible by 8:
24 / 8 = 3
Now, we can rewrite the equation as:
(3/8) * 24 = 3 * 3 = 9
This method showcases the power of simplifying fractions to streamline calculations. It's particularly helpful when dealing with larger numbers.
Method 3: Visual Representation
For a more intuitive understanding, especially for those who prefer visual aids, we can use a visual representation. Imagine a rectangle divided into 8 equal parts. Each part represents 24/8 = 3. Since we want 3/8, we simply count 3 of those parts: 3 * 3 = 9. This method is particularly useful for explaining the concept to younger learners.
Expanding the Understanding: Beyond the Basics
While finding 3/8 of 24 provides a concrete answer, it's important to appreciate the broader mathematical concepts involved. This simple problem serves as a foundation for more complex calculations:
-
Proportions: The problem can be viewed as a proportion: 3/8 = x/24. Solving for x (using cross-multiplication) will also yield the answer 9. Proportions are fundamental in various applications, from scaling recipes to calculating distances on maps.
-
Percentages: Fractions and percentages are closely related. 3/8 is equivalent to 37.5%. Therefore, finding 37.5% of 24 would also result in 9. Understanding this relationship allows for flexible problem-solving using different mathematical tools.
-
Decimals: Fractions can be expressed as decimals. 3/8 is equal to 0.375. Multiplying 0.375 by 24 also gives us 9. The ability to convert between fractions, decimals, and percentages is crucial for efficient calculations.
-
Algebra: The problem can be generalized to an algebraic expression: (a/b) * c, where 'a' is the numerator, 'b' is the denominator, and 'c' is the whole number. Understanding this generalized form helps in solving similar problems with different values.
Historical Context: The Evolution of Fractional Arithmetic
Fractions have a rich history, evolving over centuries. Ancient civilizations, including the Egyptians and Babylonians, developed their own systems for representing and working with fractions. The Egyptians, for instance, primarily used unit fractions (fractions with a numerator of 1), while the Babylonians utilized a sexagesimal system (base-60), which influenced our modern-day system of measuring time and angles. The development of efficient methods for working with fractions was a significant milestone in the advancement of mathematics and its practical applications.
Frequently Asked Questions (FAQ)
-
What if the denominator doesn't divide evenly into the whole number? In such cases, you'll get a fraction or a decimal as the answer. For example, finding 2/5 of 12 would result in 24/5, which is 4.8.
-
Can I use a calculator? Yes, absolutely! Calculators are efficient tools for solving these problems, especially when dealing with larger or more complex fractions.
-
Why is understanding this important? Understanding fractions and their application is fundamental to many aspects of life, including finance, cooking, construction, and various scientific and engineering fields. It's a building block for more advanced mathematical concepts.
-
Are there other ways to solve this problem? Yes, as demonstrated above, there are various methods, each with its own advantages and disadvantages. The best method depends on personal preference and the complexity of the problem.
Conclusion: Beyond the Simple Answer
While the answer to 3/8 of 24 is simply 9, the journey to finding that answer reveals a wealth of mathematical knowledge. This problem serves as a microcosm of the broader mathematical landscape, demonstrating the interconnectedness of fractions, percentages, decimals, proportions, and algebra. Mastering the fundamentals of fractions is not just about solving simple arithmetic problems; it's about developing a deeper understanding of the world around us and acquiring a powerful tool for problem-solving in various contexts. So, the next time you encounter a fraction, remember the journey – the understanding – is often more valuable than the final answer itself.
Latest Posts
Latest Posts
-
25 Of 250000
Sep 17, 2025
-
1 73 In Ft
Sep 17, 2025
-
35 Of 140
Sep 17, 2025
-
15 Of 33
Sep 17, 2025
-
45 Of 400
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3/8 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.