3 4 18
stanleys
Sep 12, 2025 · 6 min read
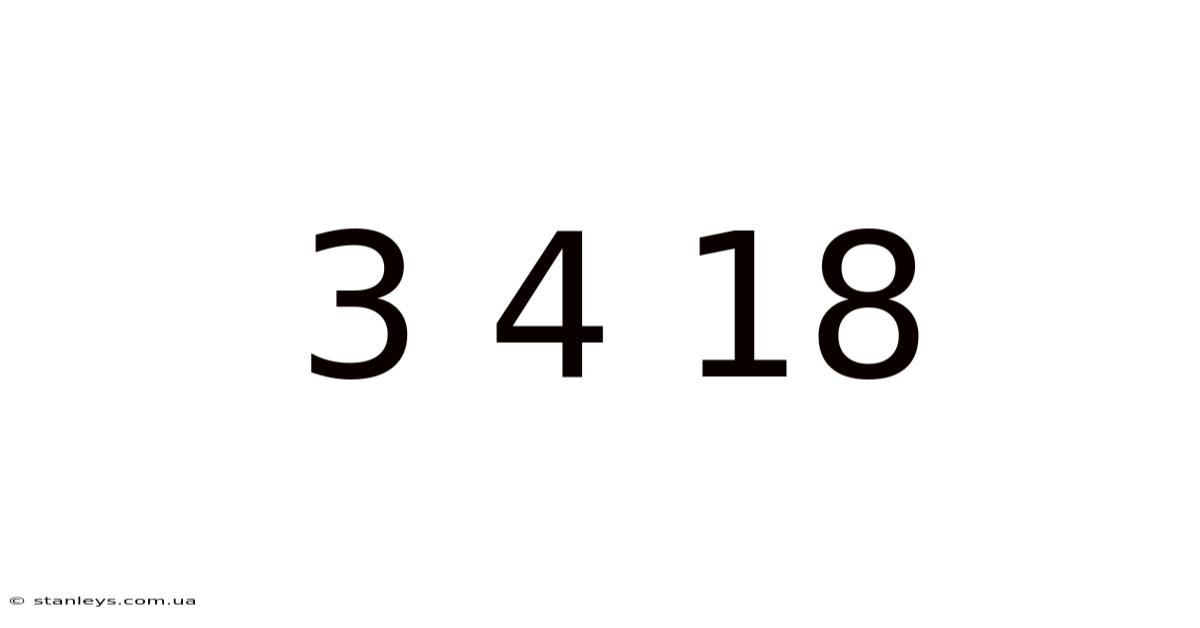
Table of Contents
Unlocking the Mysteries of 3, 4, and 18: A Deep Dive into Mathematical Relationships
The seemingly simple numbers 3, 4, and 18 hold a surprising wealth of mathematical connections and intriguing properties. This article explores these relationships, delving into various mathematical concepts to reveal the hidden connections between these three seemingly disparate numbers. We'll journey from basic arithmetic operations to more advanced concepts, uncovering the rich tapestry woven by these seemingly ordinary digits. Whether you're a mathematics enthusiast or simply curious about the fascinating world of numbers, this exploration will unveil the surprising depths hidden within 3, 4, and 18.
I. Fundamental Relationships: Arithmetic and Geometry
The most immediate relationship between 3, 4, and 18 is found in basic arithmetic.
-
Multiplication: 3 multiplied by 6 equals 18 (3 x 6 = 18). This establishes a direct multiplicative link. Furthermore, 4 multiplied by 4.5 equals 18 (4 x 4.5 = 18), demonstrating another multiplicative connection, albeit with a decimal fraction.
-
Division: 18 divided by 3 equals 6 (18 / 3 = 6), and 18 divided by 6 equals 3 (18 / 6 = 3), highlighting the inverse relationship between multiplication and division. Similarly, 18 divided by 4 equals 4.5 (18 / 4 = 4.5).
-
Geometry: The numbers 3 and 4 are fundamental in geometry. They form the legs of a right-angled triangle, the hypotenuse of which, according to the Pythagorean theorem (a² + b² = c²), is 5 (3² + 4² = 5²). While 18 doesn't directly participate in this specific right-angled triangle, it's worth noting that multiples of this 3-4-5 triangle can be constructed. For instance, a triangle with sides 6-8-10 (double the original) is also a right-angled triangle. This connection highlights the broader geometrical significance of these numbers within the framework of Pythagorean triples.
II. Factorization and Prime Numbers
Delving deeper, let's examine the factorization of these numbers:
-
3: 3 is a prime number, meaning it's only divisible by 1 and itself.
-
4: 4 is a composite number, with prime factorization 2 x 2 (2²).
-
18: 18 is a composite number, with prime factorization 2 x 3 x 3 (2 x 3²).
Notice the shared presence of the prime number 3 in both 18 and its individual components. This highlights the foundational role of prime numbers in building up composite numbers. The fact that 18 contains both 2 and 3 as prime factors connects it to both 3 and 4 at a fundamental level.
III. Exploring Number Theory Concepts
Let's explore some number theory concepts in relation to 3, 4, and 18:
-
Divisors: The divisors of 18 are 1, 2, 3, 6, 9, and 18. Notice that both 3 and 4 are not divisors of 18.
-
Modular Arithmetic: Considering modular arithmetic, we find intriguing patterns. For example, modulo 3 (the remainder after division by 3), 18 is congruent to 0 (18 ≡ 0 (mod 3)). Similarly, 18 is congruent to 2 (mod 4) because 18 divided by 4 leaves a remainder of 2.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). Neither 3, 4, nor 18 are perfect numbers. However, the concept of divisors and their sums provides a further lens through which to analyze these numbers.
IV. Patterns and Sequences
While 3, 4, and 18 don't readily form an obvious arithmetic or geometric sequence, they can be incorporated into various sequences:
-
Arithmetic Sequences: One could construct an arithmetic sequence including these numbers, for example, 3, 4, 18, 32, ... However, this is arbitrary and doesn't reveal a deep inherent mathematical relationship.
-
Geometric Sequences: Similar to arithmetic sequences, a geometric sequence can be constructed to include these numbers, but this would be an arbitrary construct rather than a natural consequence of their mathematical properties.
-
Number Triangles (Pascal's Triangle): While not directly present, the numbers 3 and 4 appear in Pascal's Triangle, highlighting their involvement in combinatorial mathematics. Though 18 isn't directly present, it's within reach in the expanding numerical patterns within Pascal's triangle.
V. Advanced Mathematical Connections
Moving beyond elementary number theory, let's explore more complex connections:
-
Algebraic Equations: One could construct various algebraic equations where 3, 4, and 18 are solutions or coefficients. However, these equations would be artificially created and not reflect an intrinsic mathematical relationship between the numbers.
-
Higher-Dimensional Geometry: While 3 and 4 have clear geometric significance in two dimensions (the Pythagorean theorem), expanding into higher dimensions adds complexity. The number 18 doesn’t immediately translate to simple higher-dimensional geometric concepts in an obvious way.
-
Number Systems: The numbers 3, 4, and 18 maintain their fundamental properties across different number systems (binary, hexadecimal, etc.), highlighting their inherent mathematical properties independent of the system of representation.
VI. Practical Applications and Real-World Examples
While the abstract mathematical relationships between 3, 4, and 18 may seem theoretical, they subtly appear in various real-world applications:
-
Construction and Engineering: The 3-4-5 triangle (and its multiples) is widely used in construction and engineering for establishing right angles.
-
Calendars: The number 3 appears frequently in calendar systems (30-day months, 365-day year). The number 4 also finds application in the weekly calendar. The number 18, though less prevalent, still has potential use in various calendar applications or calculations of time periods.
VII. Frequently Asked Questions (FAQ)
Q: Is there a specific mathematical formula or theorem connecting 3, 4, and 18 directly?
A: There isn't a single, established formula or theorem specifically linking these three numbers. Their relationships are primarily observed through basic arithmetic operations, factorization, and contextual applications within broader mathematical concepts.
Q: Are there any significant unsolved problems related to these numbers?
A: No, there are no significant, unsolved mathematical problems directly centered on these three numbers. Their connections are primarily explored within established mathematical frameworks.
Q: Can these numbers be used to create a unique mathematical puzzle or game?
A: Yes, one could design mathematical puzzles or games involving these numbers. For instance, a puzzle could involve finding different ways to combine these numbers through arithmetic operations to reach a target number.
VIII. Conclusion
This exploration of the numbers 3, 4, and 18 reveals that the apparent simplicity belies a surprising richness in mathematical relationships. While there isn't one overarching theorem that defines their connection, exploring them through different lenses – arithmetic, geometry, number theory – reveals a fascinating tapestry of connections. The journey demonstrates the interconnectedness of mathematical concepts and highlights how even seemingly simple numbers can lead to profound explorations of the numerical world. Further investigation could involve exploring the numbers' appearance in different number systems or extending the analysis to similar number trios to discover common patterns and relationships. The inherent beauty of mathematics lies in these explorations, encouraging us to look deeper and discover the hidden wonders embedded within seemingly ordinary numbers.
Latest Posts
Latest Posts
-
5 6 In Fraction
Sep 12, 2025
-
82 7kg In Stones
Sep 12, 2025
-
Semi Interquartile Range
Sep 12, 2025
-
Synonyms Of Applicability
Sep 12, 2025
-
1 000 5
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 4 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.