27 X 3
stanleys
Sep 16, 2025 · 5 min read
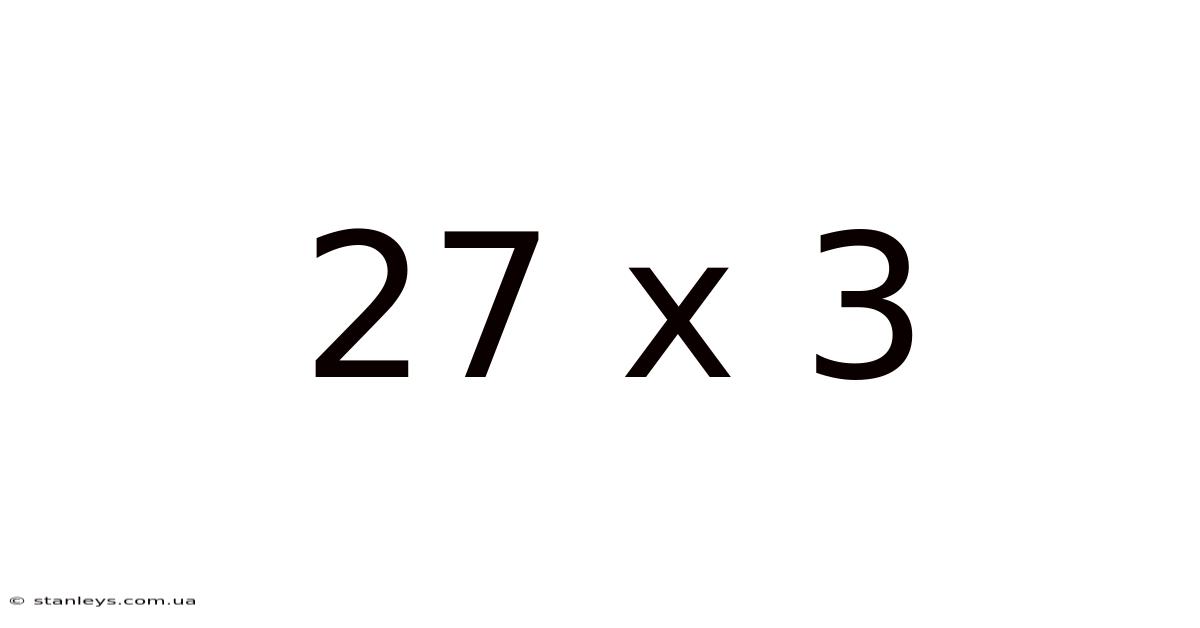
Table of Contents
Unveiling the Wonders of 27 x 3: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem 27 x 3, delving far beyond the immediate answer. We'll unpack various methods of solving this problem, examining the underlying mathematical principles, exploring real-world applications, and even touching upon the historical context of multiplication itself. Understanding 27 x 3 isn't just about finding the product; it's about developing a deeper understanding of numerical relationships and problem-solving strategies.
Introduction: More Than Just a Number
At first glance, 27 x 3 appears straightforward. Even young students can grasp the concept of repeated addition: 27 + 27 + 27. However, this seemingly simple equation serves as a gateway to understanding more complex mathematical concepts. This article aims to demystify the process, showcasing different approaches to solving 27 x 3 and highlighting the importance of mathematical fluency. We will cover traditional methods, alternative strategies, and even explore the problem's potential within the context of advanced mathematical concepts.
Method 1: Traditional Multiplication
This is the method most of us learned in elementary school. It involves breaking down the numbers into tens and ones, then multiplying and adding the results.
- Step 1: Multiply the ones: 3 x 7 = 21. Write down "1" and carry-over "2".
- Step 2: Multiply the tens: 3 x 2 = 6. Add the carry-over "2": 6 + 2 = 8.
- Step 3: Combine the results: The final answer is 81.
Therefore, 27 x 3 = 81. This method demonstrates a fundamental understanding of place value and the distributive property of multiplication.
Method 2: Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to solve 27 x 3:
- Rewrite 27 as 20 + 7.
- Apply the distributive property: 3 x (20 + 7) = (3 x 20) + (3 x 7)
- Calculate: (60) + (21) = 81
This approach reinforces the understanding of how multiplication works at a deeper level, showcasing the relationship between addition and multiplication.
Method 3: Repeated Addition
This is the most intuitive method, especially for younger learners. It involves adding 27 three times:
27 + 27 + 27 = 81
While simple, this method highlights the fundamental relationship between addition and multiplication. It’s a valuable tool for building a strong foundation in arithmetic.
Method 4: Doubling and Halving
This method involves strategically manipulating the numbers to simplify the calculation. While not always the most efficient for 27 x 3, it's a useful technique for larger numbers.
- Double 27: 27 x 2 = 54
- Half 3: 3 / 2 = 1.5 (This step leads to a decimal which complicates this specific problem)
In this case, doubling and halving isn't the most efficient method for this specific problem due to the resulting decimal. However, it demonstrates a flexible approach to problem-solving, crucial for more complex mathematical operations.
Method 5: Using a Multiplication Table
A multiplication table provides a quick reference for basic multiplication facts. By looking up 27 (though usually tables only go up to 12) and 3, you can quickly find the product: 81. While convenient for simpler problems, understanding the underlying methods is crucial for solving more complex equations.
The Mathematical Principles at Play
Solving 27 x 3 involves several core mathematical principles:
- Place Value: The method of breaking down 27 into tens and ones demonstrates a deep understanding of place value, a fundamental concept in arithmetic.
- Distributive Property: The distributive property of multiplication over addition is crucial for understanding how multiplication interacts with addition.
- Commutative Property: Although not explicitly used here, the commutative property (a x b = b x a) highlights that the order of multiplication doesn't affect the result (3 x 27 = 27 x 3).
- Associative Property: Similarly, the associative property (a x (b x c) = (a x b) x c) plays a role in understanding how we can group numbers during complex multiplications.
Real-World Applications of Multiplication
The ability to quickly and accurately perform multiplication like 27 x 3 is essential in numerous real-world scenarios:
- Shopping: Calculating the total cost of multiple items. For example, buying three items that cost $27 each.
- Cooking: Scaling recipes up or down. If a recipe calls for 27 grams of flour, and you need to triple the recipe.
- Construction: Calculating material needs. If a project requires 27 units of a certain material, and you need three times that amount.
- Finance: Calculating interest or discounts.
- Everyday problem-solving: A wide range of everyday situations require basic multiplication skills for quick and accurate calculations.
Exploring Beyond the Basics: Extending the Concept
While 27 x 3 is a basic multiplication problem, it can serve as a stepping stone to more complex mathematical concepts:
- Algebra: The problem can be expressed algebraically as 3x = 81, where 'x' represents the unknown number 27.
- Calculus: While not directly applicable, understanding multiplication forms the foundation for more advanced mathematical concepts like derivatives and integrals.
- Number Theory: Exploring the factors and multiples of 81 (the product) can lead to an understanding of number theory concepts.
Frequently Asked Questions (FAQs)
Q: What is the quickest way to solve 27 x 3?
A: The traditional multiplication method (as described in Method 1) is usually the quickest and most efficient for this particular problem. However, for larger numbers, other methods might be more efficient.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental operation in mathematics, essential for countless real-world applications and for building a strong foundation for more advanced mathematical concepts.
Q: Are there other ways to visualize 27 x 3?
A: Yes! You could use visual aids like arrays (a grid of 27 rows and 3 columns) or manipulatives (like blocks or counters) to physically represent the multiplication.
Conclusion: Mastering the Fundamentals
The seemingly simple problem 27 x 3 offers a window into the fascinating world of mathematics. By exploring various solution methods and understanding the underlying mathematical principles, we gain a much deeper appreciation for the power and elegance of multiplication. Mastering this fundamental operation is not just about getting the right answer; it's about building a solid foundation for future mathematical endeavors and developing crucial problem-solving skills applicable to numerous aspects of life. From everyday calculations to advanced mathematical concepts, the understanding gleaned from solving 27 x 3 has far-reaching implications. Continue to explore and expand your mathematical knowledge; the journey is as rewarding as the destination.
Latest Posts
Related Post
Thank you for visiting our website which covers about 27 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.