252 Of 120
stanleys
Sep 10, 2025 · 5 min read
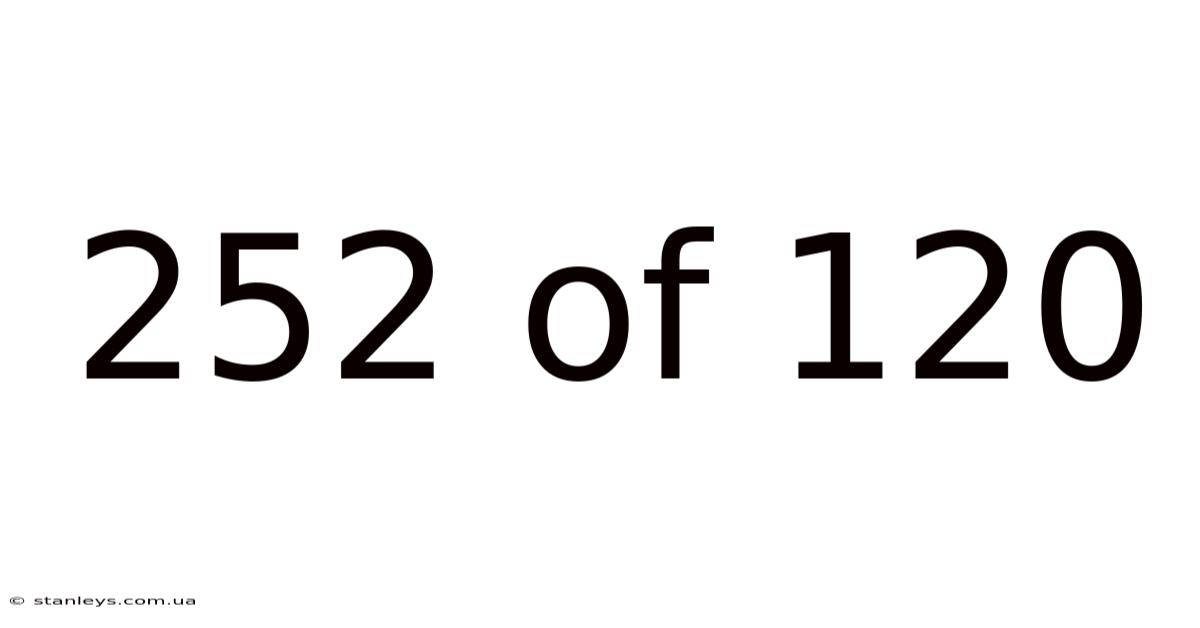
Table of Contents
Understanding the Fraction 252/120: Simplification, Decimal Conversion, and Real-World Applications
The fraction 252/120 might seem daunting at first glance, but understanding its components and how to manipulate it is crucial for various mathematical applications. This comprehensive guide will explore the simplification of this fraction, its decimal equivalent, and provide real-world examples to illustrate its practical use. We'll break down the process step-by-step, making it accessible to learners of all levels.
Introduction: Deconstructing the Fraction
The fraction 252/120 represents a part-to-whole relationship. The numerator (252) indicates the number of parts we're considering, while the denominator (120) represents the total number of equal parts that make up the whole. Before we delve deeper, let's establish the core concepts:
- Numerator: The top number in a fraction (252 in this case).
- Denominator: The bottom number in a fraction (120 in this case).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator. 252/120 is an improper fraction.
- Simplification (or Reduction): The process of finding an equivalent fraction with a smaller numerator and denominator.
Step-by-Step Simplification of 252/120
The key to simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers without leaving a remainder. Let's find the GCD of 252 and 120 using the prime factorization method:
-
Prime Factorization of 252: 252 = 2 x 126 = 2 x 2 x 63 = 2 x 2 x 3 x 21 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7
-
Prime Factorization of 120: 120 = 2 x 60 = 2 x 2 x 30 = 2 x 2 x 2 x 15 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
-
Identifying Common Factors: We look for the common prime factors in both factorizations: 2 and 3.
-
Calculating the GCD: The GCD is found by multiplying the lowest power of each common prime factor. In this case, it's 2¹ x 3¹ = 6.
-
Simplifying the Fraction: We divide both the numerator and the denominator by the GCD (6):
252 ÷ 6 = 42 120 ÷ 6 = 20
Therefore, the simplified fraction is 42/20. However, we can simplify further. Notice that both 42 and 20 are divisible by 2:
42 ÷ 2 = 21 20 ÷ 2 = 10
Thus, the fully simplified fraction is 21/10.
Converting the Fraction to a Decimal
To convert the simplified fraction 21/10 to a decimal, we simply perform the division:
21 ÷ 10 = 2.1
Therefore, the decimal equivalent of 252/120 is 2.1.
Understanding Mixed Numbers
Since 21/10 is an improper fraction (numerator > denominator), we can also express it as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 21/10 to a mixed number:
-
Divide the numerator (21) by the denominator (10): 21 ÷ 10 = 2 with a remainder of 1.
-
The whole number part of the mixed number is the quotient (2).
-
The fractional part is the remainder (1) over the original denominator (10).
So, 21/10 as a mixed number is 2 1/10.
Real-World Applications of Fractions like 252/120
Fractions are fundamental to many real-world scenarios. Let's consider some examples where a fraction like 252/120 (or its simplified form 21/10) could be applicable:
-
Baking: Imagine a recipe calling for 252 grams of flour for 120 cookies. The fraction 252/120 represents the amount of flour per cookie. Simplifying it to 21/10 (or 2.1) tells us that each cookie requires 2.1 grams of flour.
-
Construction: Suppose a construction project requires 252 meters of wire for 120 light fixtures. The fraction 252/120 simplifies to 2.1, indicating that each light fixture needs 2.1 meters of wire.
-
Finance: If you earned $252 over 120 hours of work, the fraction 252/120 represents your hourly wage. Simplifying it to 2.1 shows you earned $2.10 per hour.
-
Sports Statistics: Consider a basketball player who made 252 shots out of 120 attempts. The fraction 252/120 simplifies to 2.1, representing an average of 2.1 successful shots per attempt (a remarkably high success rate!).
-
Data Analysis: In analyzing survey results, imagine 252 respondents out of 1200 chose a particular option. The fraction 252/1200 can be simplified to 21/100, representing 21% of respondents who selected that option.
Frequently Asked Questions (FAQ)
-
Why is simplifying fractions important? Simplifying fractions makes them easier to understand and work with. It provides a more concise representation of the same value.
-
What if I don't get the GCD right away? It's okay to simplify in multiple steps. Keep dividing the numerator and denominator by common factors until you reach the simplest form.
-
Can I use a calculator to simplify fractions? Many calculators have built-in functions for finding the GCD and simplifying fractions.
-
Are there other methods to find the GCD besides prime factorization? Yes, the Euclidean algorithm is another efficient method for finding the greatest common divisor.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is a cornerstone of mathematical literacy. This detailed exploration of 252/120 demonstrates the importance of simplification and conversion between fractions and decimals. By mastering these techniques, you'll be better equipped to tackle various mathematical problems and apply your knowledge to numerous real-world situations. Remember, consistent practice and a clear understanding of the underlying principles are key to success in mastering fractions and other mathematical concepts. Don't be afraid to explore further and experiment with different fractions – the more you practice, the more confident and proficient you'll become!
Latest Posts
Latest Posts
-
60ml In Tablespoons
Sep 10, 2025
-
3 Of 9000
Sep 10, 2025
-
Half Of 365
Sep 10, 2025
-
38cm To Inches
Sep 10, 2025
-
Specialisation Of Labour
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 252 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.