2500 / 3
stanleys
Sep 10, 2025 · 6 min read
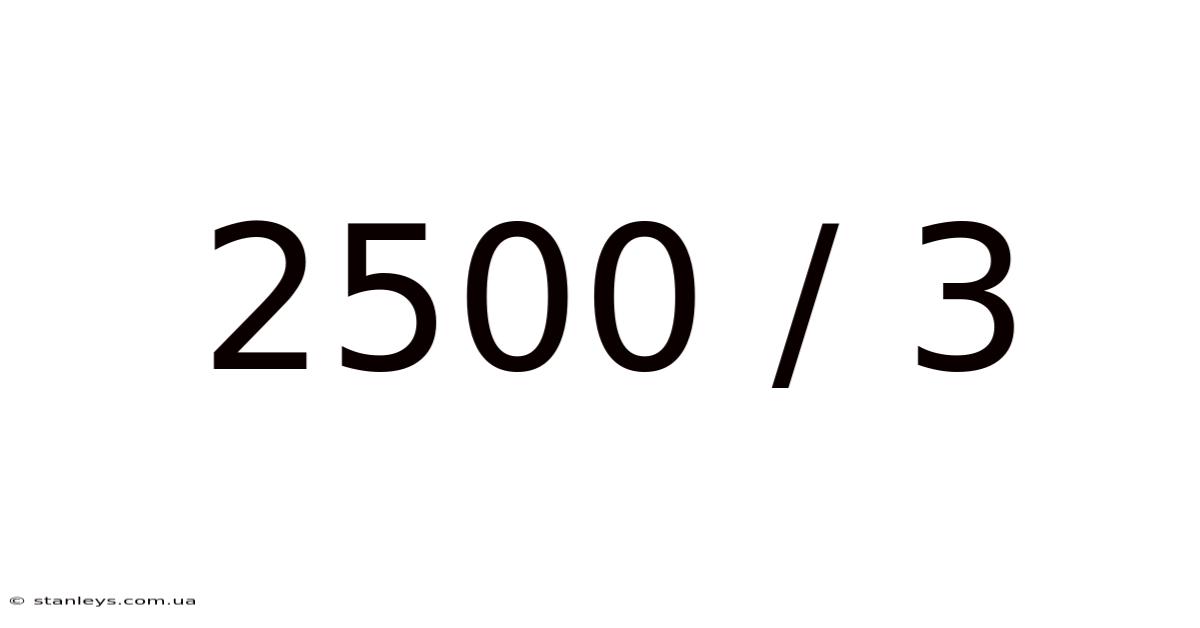
Table of Contents
Decoding 2500/3: A Deep Dive into Division and Its Applications
This article explores the mathematical operation of division, specifically focusing on the problem 2500/3. We'll break down the process, examine different approaches to solving it, discuss its applications in various fields, and address common questions surrounding division. Understanding division is fundamental to various aspects of mathematics, science, and everyday life, making this topic both practical and enriching.
Understanding Division: A Fundamental Operation
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts or groups. The problem 2500/3 asks: "How many times does 3 fit into 2500?" The number 2500 is the dividend, the number 3 is the divisor, and the result is the quotient. In division, we may also encounter a remainder, which represents the portion of the dividend that's left over after the division is complete.
Methods for Solving 2500/3
There are several ways to solve 2500/3, each offering different insights into the problem:
1. Long Division
Long division is a traditional method that systematically breaks down the division process into smaller, manageable steps.
- Step 1: Set up the long division problem: 3 | 2500
- Step 2: Divide the first digit (2) by the divisor (3). Since 2 is smaller than 3, we move to the next digit.
- Step 3: Divide 25 by 3. 3 goes into 25 eight times (3 x 8 = 24). Write 8 above the 5.
- Step 4: Subtract 24 from 25, leaving a remainder of 1.
- Step 5: Bring down the next digit (0).
- Step 6: Divide 10 by 3. 3 goes into 10 three times (3 x 3 = 9). Write 3 above the 0.
- Step 7: Subtract 9 from 10, leaving a remainder of 1.
- Step 8: Bring down the next digit (0).
- Step 9: Divide 10 by 3. 3 goes into 10 three times (3 x 3 = 9). Write 3 above the 0.
- Step 10: Subtract 9 from 10, leaving a remainder of 1.
Therefore, 2500 divided by 3 is 833 with a remainder of 1. This can be expressed as 833 R 1 or 833 ¹/₃.
2. Using a Calculator
The simplest way to solve 2500/3 is using a calculator. Simply input 2500 ÷ 3 and the calculator will display the result: 833.333333... This is a decimal representation, showing that the division results in a non-terminating repeating decimal.
3. Fraction Representation
The result can also be expressed as a mixed number: 833 ¹/₃. This clearly shows the whole number part (833) and the fractional remainder (¹/₃).
Applications of Division: Real-World Examples
Division is an essential tool in numerous fields and everyday scenarios:
-
Sharing Equally: If you have 2500 candies and want to distribute them equally among 3 friends, division helps determine how many candies each friend receives (833 with one candy leftover).
-
Averaging: Calculating the average speed, temperature, or any other quantity involves division. For instance, if a car travels 2500 km in 3 days, the average daily distance is 2500/3 = 833.33 km/day.
-
Unit Conversion: Converting units often requires division. For example, converting 2500 centimeters to meters involves dividing by 100 (2500/100 = 25 meters).
-
Finance: Division is crucial in calculating percentages, interest rates, profit margins, and splitting costs among multiple parties.
-
Engineering and Physics: Many engineering and physics calculations rely heavily on division, from calculating forces and velocities to determining material properties and designing structures.
-
Computer Science: Division is a fundamental operation in computer programming and algorithms, used in tasks like array indexing, data manipulation, and resource allocation.
-
Data Analysis: In statistics and data analysis, division is used to calculate ratios, proportions, and averages.
Understanding Decimal and Fractional Representations
The solution 833.333... represents a recurring decimal. The '3' repeats infinitely. This is because 1/3 cannot be expressed as a terminating decimal. The fraction 833 ¹/₃ provides a more precise representation, avoiding the need for an infinite decimal expansion. Choosing between decimal and fraction representation depends on the context and the level of precision required. For many practical applications, rounding the decimal (e.g., to 833.33) might be sufficient.
Beyond 2500/3: Exploring Division with Different Numbers
The principles applied to solving 2500/3 can be generalized to other division problems. Understanding the process, regardless of the numbers involved, is key. Consider these examples:
-
Dividing by a larger number: If the divisor is larger than the dividend (e.g., 3/2500), the result will be a decimal less than 1.
-
Dividing by a power of 10: Dividing by 10, 100, 1000, etc., simply involves moving the decimal point to the left.
-
Dividing by fractions: Dividing by a fraction is equivalent to multiplying by its reciprocal. For example, 2500 divided by 1/3 is the same as 2500 multiplied by 3, which equals 7500.
Frequently Asked Questions (FAQ)
Q: What if I get a remainder in division?
A: A remainder indicates that the dividend is not perfectly divisible by the divisor. The remainder can be expressed as a fraction (e.g., ¹/₃) or as a decimal (e.g., 0.333...). The choice depends on the level of accuracy needed.
Q: How can I improve my division skills?
A: Practice is key! Start with simple division problems and gradually increase the difficulty. Utilize different methods (long division, calculator, etc.) to strengthen your understanding and find the most efficient approach for you.
Q: Why is division important in everyday life?
A: Division helps us solve problems related to sharing, averaging, proportions, and many other scenarios that we encounter daily, from splitting bills to calculating fuel consumption.
Q: What are some common mistakes to avoid in division?
A: Common mistakes include misplacing digits during long division, incorrectly interpreting remainders, and failing to consider the context of the problem. Careful attention to detail and a clear understanding of the process can help avoid these errors.
Conclusion: Mastering Division for a Brighter Future
Division, while seemingly a simple arithmetic operation, is a powerful tool with far-reaching applications. Mastering division not only improves your mathematical skills but also enhances your ability to solve problems in various fields and everyday life. By understanding different methods of solving division problems, such as long division and utilizing calculators, and appreciating the significance of both decimal and fractional representations, you equip yourself with a vital skill for academic success and navigating the complexities of the real world. The seemingly simple problem of 2500/3 reveals the depth and importance of this fundamental operation, laying the groundwork for more advanced mathematical concepts and problem-solving strategies. Continue to practice and explore the wonders of division!
Latest Posts
Latest Posts
-
46kg To Stone
Sep 10, 2025
-
64cm In Inches
Sep 10, 2025
-
99 2f To C
Sep 10, 2025
-
6 7 2
Sep 10, 2025
-
3000m To Miles
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 2500 / 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.