25 Of 85
stanleys
Sep 21, 2025 · 5 min read
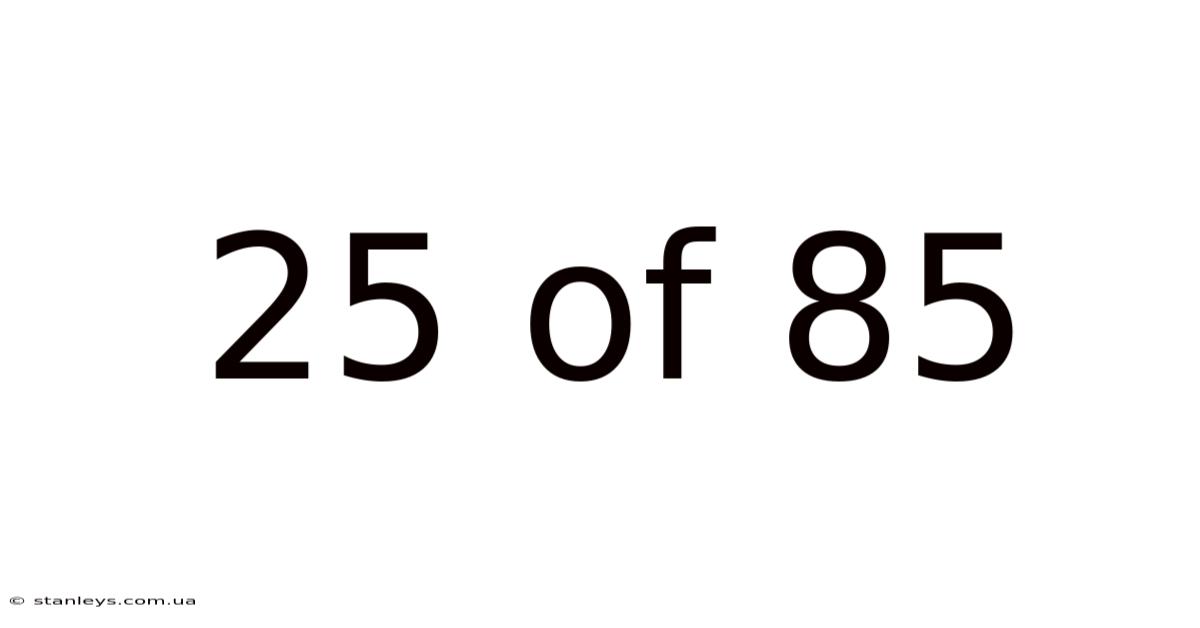
Table of Contents
Decoding the Enigma: Understanding and Applying the Fraction 25/85
The seemingly simple fraction 25/85 might appear unremarkable at first glance. However, beneath its unassuming exterior lies a world of mathematical concepts and practical applications that extend far beyond basic arithmetic. This article delves deep into the intricacies of 25/85, exploring its simplification, decimal representation, percentage equivalent, real-world applications, and even its connection to broader mathematical principles. We'll unravel its secrets, revealing its hidden potential and demonstrating its relevance in various fields. This comprehensive guide will equip you with a complete understanding of this fraction and its significance.
Introduction: Unpacking the Fraction 25/85
The fraction 25/85 represents a part-to-whole relationship. It signifies that we are considering 25 units out of a total of 85 units. This basic understanding forms the foundation for exploring its various properties and applications. While seemingly straightforward, this fraction provides a valuable opportunity to explore fundamental mathematical concepts and develop a deeper appreciation for fractional arithmetic. Understanding this seemingly simple fraction can unlock a deeper understanding of more complex mathematical concepts.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before diving into its other properties, let's simplify 25/85 to its lowest terms. This process involves finding the greatest common divisor (GCD) of both the numerator (25) and the denominator (85). The GCD is the largest number that divides both 25 and 85 without leaving a remainder.
- Finding the factors of 25: 1, 5, 25
- Finding the factors of 85: 1, 5, 17, 85
Notice that the greatest common factor between 25 and 85 is 5. Therefore, we can simplify the fraction by dividing both the numerator and the denominator by 5:
25 ÷ 5 = 5 85 ÷ 5 = 17
Thus, the simplified form of 25/85 is 5/17. This simplified form is essential for easier calculations and a clearer understanding of the fraction's value.
Decimal Representation: Converting a Fraction to a Decimal
Converting the fraction 5/17 to its decimal equivalent involves dividing the numerator (5) by the denominator (17). This process results in a repeating decimal:
5 ÷ 17 ≈ 0.294117647...
The decimal representation of 5/17 is an irrational number because it is a non-terminating, non-repeating decimal. This means that the digits after the decimal point continue infinitely without a repeating pattern. For practical purposes, we often round the decimal to a specific number of decimal places. Rounding to three decimal places, we get 0.294.
Percentage Equivalent: Expressing the Fraction as a Percentage
To express the fraction 5/17 as a percentage, we multiply the decimal equivalent by 100:
0.294117647... × 100 ≈ 29.41%
Therefore, 25/85, or its simplified form 5/17, is approximately 29.41%. This percentage representation provides a convenient way to understand the relative size of the fraction compared to the whole.
Real-World Applications: Seeing 25/85 in Action
The fraction 25/85, or its simplified version 5/17, appears in various real-world scenarios. Here are a few examples:
- Proportions and Ratios: Imagine a class with 85 students, and 25 of them are girls. The fraction 25/85 (or 5/17) represents the proportion of girls in the class.
- Probability: If you have a bag containing 85 marbles, 25 of which are red, the probability of drawing a red marble is 25/85 (or 5/17).
- Measurement and Scaling: If you need to reduce a drawing by a scale factor of 5/17, you would multiply all dimensions by this fraction.
- Financial Calculations: In finance, fractions are frequently used to represent parts of a whole, such as calculating shares of a company or portions of an investment portfolio. 25/85 could represent a portion of a total investment.
Further Mathematical Exploration: Connections to Other Concepts
The fraction 25/85 provides a springboard for exploring several advanced mathematical concepts:
- Continued Fractions: The fraction 5/17 can be represented as a continued fraction, offering a unique way to express the ratio. Continued fractions are valuable in number theory and approximation.
- Modular Arithmetic: In modular arithmetic, the remainder after division is crucial. The fraction's decimal representation and its remainder when divided by various numbers are relevant in this area.
- Rational Numbers: The fraction 5/17 is a rational number, which means it can be expressed as the ratio of two integers. Understanding rational numbers is essential for various mathematical fields.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 25/85?
A1: The simplest form of 25/85 is 5/17. This is achieved by dividing both the numerator and the denominator by their greatest common divisor, which is 5.
Q2: Is 25/85 a proper or improper fraction?
A2: 25/85 is a proper fraction because the numerator (25) is smaller than the denominator (85). Proper fractions represent values less than 1.
Q3: How do I convert 25/85 to a percentage?
A3: First, simplify the fraction to 5/17. Then, divide the numerator (5) by the denominator (17) to get the decimal equivalent (approximately 0.294). Finally, multiply the decimal by 100 to obtain the percentage (approximately 29.4%).
Q4: What are some real-world applications of 25/85?
A4: The fraction 25/85, or 5/17, can be used in various contexts, such as calculating proportions, probabilities, scaling drawings, and representing parts of a whole in financial calculations.
Conclusion: The Significance of Understanding Fractions
While seemingly insignificant, the fraction 25/85 offers a rich learning experience. Its simplification, decimal and percentage conversions, and real-world applications highlight the importance of understanding fundamental fractional arithmetic. This fraction serves as a microcosm of broader mathematical principles, demonstrating the interconnectedness of various mathematical concepts. Mastering the manipulation and interpretation of fractions like 25/85 forms a crucial foundation for more advanced mathematical studies and practical problem-solving in numerous fields. By thoroughly understanding this seemingly simple fraction, you gain a deeper appreciation for the power and elegance of mathematics in its various applications. The seemingly simple fraction 25/85, therefore, becomes a gateway to a broader understanding of the mathematical world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 25 Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.