25 Of 50
stanleys
Sep 14, 2025 · 6 min read
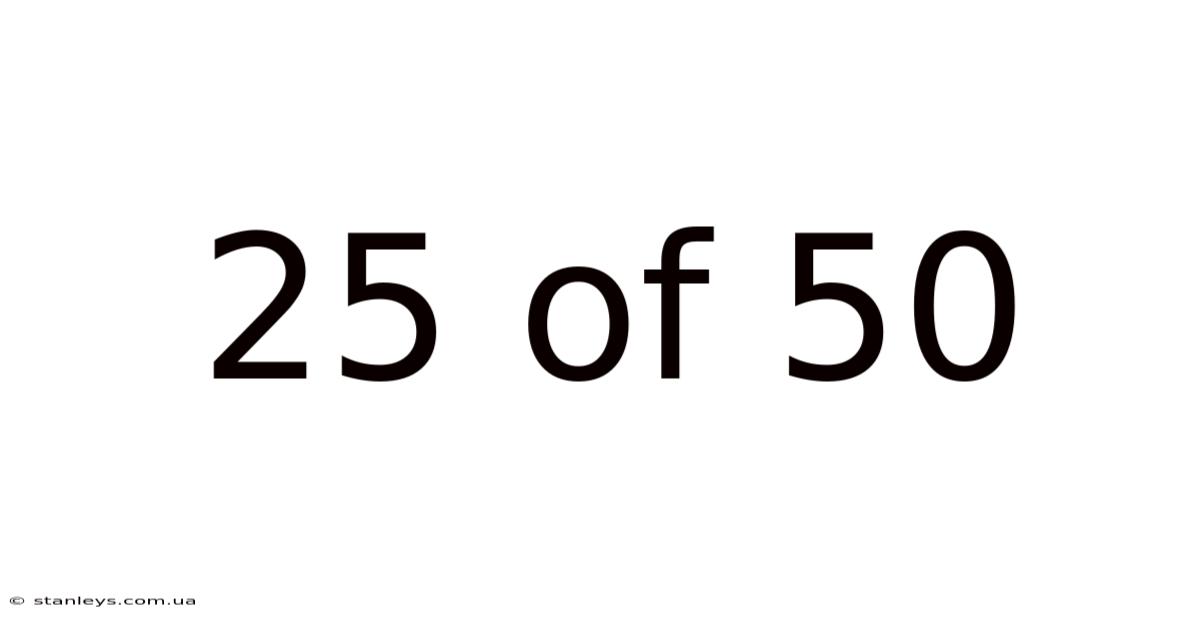
Table of Contents
Decoding the Enigma: Understanding the Fraction 25/50 and its Broader Implications
The seemingly simple fraction 25/50 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a deeper appreciation of mathematical concepts like simplification, percentages, ratios, and their applications in real-world scenarios. This article will delve into the intricacies of 25/50, exploring its simplification, equivalent forms, percentage representation, practical applications, and addressing frequently asked questions. By the end, you'll not only understand 25/50 but also gain a broader understanding of fractional arithmetic and its relevance.
Introduction: The Significance of Simplifying Fractions
Fractions represent parts of a whole. The fraction 25/50 means 25 out of 50 equal parts. While this is a perfectly valid representation, mathematics emphasizes simplification to express fractions in their most concise and understandable form. Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator (25) and the denominator (50) and dividing both by it. This process doesn't change the value of the fraction; it simply presents it more efficiently.
Simplifying 25/50: A Step-by-Step Guide
Let's simplify 25/50.
-
Find the GCD: The greatest common divisor of 25 and 50 is 25. This means that both 25 and 50 are divisible by 25 without leaving a remainder.
-
Divide both numerator and denominator: Dividing both the numerator (25) and the denominator (50) by 25, we get:
25 ÷ 25 = 1 50 ÷ 25 = 2
-
Simplified Fraction: Therefore, the simplified form of 25/50 is 1/2.
This simplification process reveals that 25/50 represents exactly half of a whole.
Equivalent Fractions: Exploring Different Representations
While 1/2 is the simplest form, 25/50 is one of many fractions equivalent to 1/2. Equivalent fractions represent the same proportion or value but have different numerators and denominators. You can create equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example:
- Multiplying by 2: (1/2) * (2/2) = 2/4
- Multiplying by 3: (1/2) * (3/3) = 3/6
- Multiplying by 4: (1/2) * (4/4) = 4/8
- And so on...
Conversely, you can obtain 1/2 by dividing both the numerator and denominator of a larger equivalent fraction by the same number. For instance, 100/200 simplifies to 1/2 by dividing both by 100. Understanding equivalent fractions is crucial in comparing and manipulating fractions in various mathematical operations.
Percentage Representation: Connecting Fractions to Percentages
Percentages provide another way to express fractions. A percentage represents a fraction with a denominator of 100. To convert a fraction to a percentage, you divide the numerator by the denominator and multiply the result by 100. In the case of 25/50 (or its simplified form, 1/2):
-
Divide numerator by denominator: 1 ÷ 2 = 0.5
-
Multiply by 100: 0.5 * 100 = 50
Therefore, 25/50 is equal to 50%. This means that 25/50 represents 50 out of every 100 parts, or one-half.
Ratio Representation: Understanding Proportions
A ratio expresses the relative size of two or more values. The fraction 25/50 can be expressed as a ratio of 25:50, which simplifies to 1:2. This ratio indicates that for every one part of a specific quantity, there are two parts of another. For example, if you have a bag containing 25 red marbles and 25 blue marbles, the ratio of red marbles to blue marbles is 1:1 (25:25, simplified). However, if you were to consider the ratio of red marbles to the total number of marbles (50), it would be 25:50 or 1:2. Understanding ratios is crucial in various fields, including recipe scaling, map interpretation, and statistical analysis.
Practical Applications: Real-World Examples
The fraction 25/50, or its equivalent 1/2, appears frequently in everyday life. Here are a few examples:
-
Sharing Equally: If you have 50 candies and want to share them equally with a friend, you'll each receive 25 candies, representing 25/50 or 1/2 of the total.
-
Discount Calculations: A 50% discount means you pay half the original price, mirroring the fraction 1/2.
-
Measurement Conversions: Converting units often involves fractions. For example, half a meter is 0.5 meters, which is equivalent to 25/50 of a meter.
-
Probability: In probability, 1/2 represents the probability of a coin landing on heads or tails (assuming a fair coin). This is equivalent to a 50% chance.
-
Data Analysis: In statistical analysis and data visualization, half of a dataset could be represented as 25/50, signifying a critical point or median within the data.
Deeper Dive: Exploring Decimal Equivalents and Beyond
The fraction 25/50 is also easily represented as a decimal: 0.5. Decimals offer another way to understand the value of fractions, particularly when dealing with calculations involving other decimal numbers. The decimal equivalent helps visualize the fraction's position on the number line.
Further explorations could include looking at the fraction's representation in other number systems (e.g., binary) or its application in more advanced mathematical concepts like complex numbers or calculus. The fundamental understanding of 25/50, however, forms a solid base for exploring such complexities.
Frequently Asked Questions (FAQs)
Q1: Is 25/50 the only way to represent half?
No, there are infinitely many equivalent fractions representing one-half, such as 1/2, 2/4, 3/6, 50/100, etc. However, 1/2 is the simplest and most commonly used form.
Q2: Why is simplifying fractions important?
Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the value in its most concise and efficient form.
Q3: How can I convert any fraction to a percentage?
To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100.
Q4: What is the difference between a fraction and a ratio?
While both fractions and ratios represent parts of a whole or comparisons between quantities, a fraction represents a single part of a whole, while a ratio can compare multiple quantities. A fraction is always a part of the whole, whereas a ratio can be a comparison between parts of a whole or between entirely separate quantities.
Q5: Can I use a calculator to simplify fractions?
Yes, many calculators have functions that simplify fractions. However, understanding the manual process of finding the GCD and simplifying is important for building a strong mathematical foundation.
Conclusion: Beyond the Basics of 25/50
The seemingly simple fraction 25/50 opens doors to a deeper understanding of fundamental mathematical concepts. Its simplification to 1/2 highlights the importance of efficiency in mathematical representation. Exploring its equivalent forms, percentage, and ratio representations expands our understanding of proportional relationships and their applications in various contexts. This seemingly simple fraction serves as a powerful tool to demonstrate the interconnectedness of different mathematical concepts and their relevance in real-world scenarios. From basic arithmetic to more advanced mathematical concepts, the principles demonstrated by 25/50 lay a solid groundwork for further exploration and learning. Remember, a deep understanding of the basics is the key to unlocking more complex mathematical ideas.
Latest Posts
Latest Posts
-
Composers From Russia
Sep 14, 2025
-
70 Of 8
Sep 14, 2025
-
5 X 6
Sep 14, 2025
-
Hdmi 2 Cable
Sep 14, 2025
-
21lb In Kg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.