25 Of 4
stanleys
Sep 17, 2025 · 6 min read
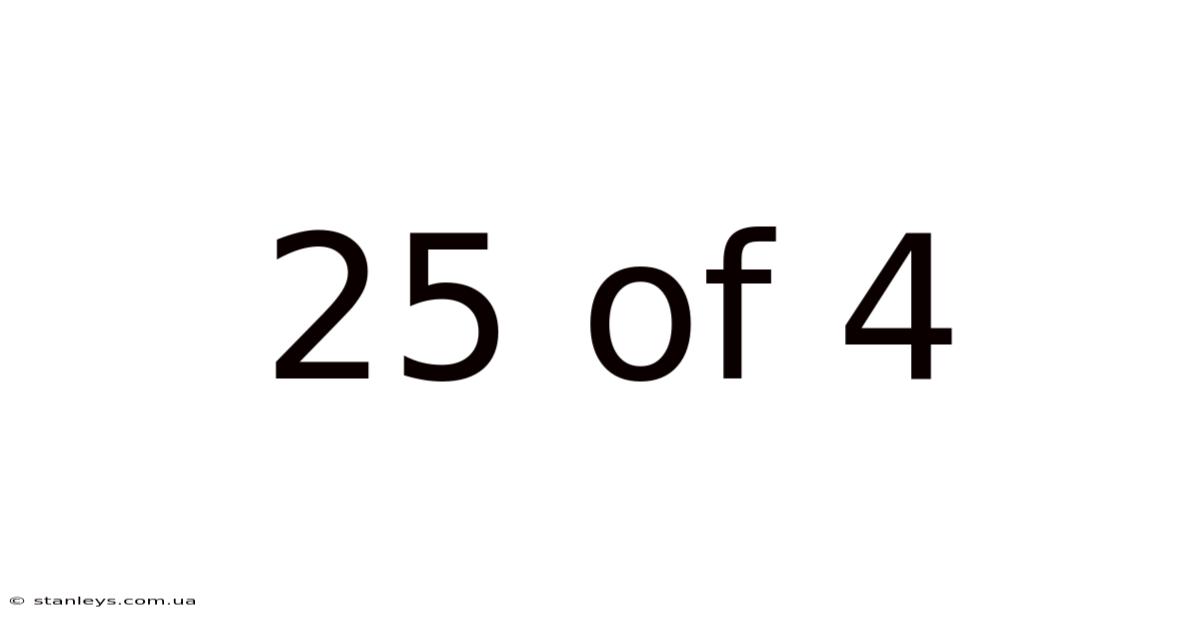
Table of Contents
Decoding the Fraction 25/4: A Comprehensive Guide
Understanding fractions is a cornerstone of mathematical literacy. This article delves deep into the fraction 25/4, exploring its various representations, applications, and the underlying concepts that govern its manipulation. We'll move beyond simple calculation to explore the deeper meaning and significance of this seemingly simple fraction. This guide is designed for learners of all levels, from those just grasping the basics of fractions to those seeking a more nuanced understanding. Whether you're a student struggling with fractions or an adult looking to refresh your mathematical knowledge, this comprehensive guide will provide a clear and engaging path to mastery.
Understanding Fractions: A Quick Refresher
Before we dive into 25/4, let's quickly review the fundamental components of a fraction. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number (25 in our case) indicates how many parts we have.
- Denominator: The bottom number (4 in our case) indicates how many equal parts the whole is divided into.
Therefore, 25/4 signifies that we have 25 parts of a whole that's been divided into 4 equal parts. This representation immediately suggests that we have more than the whole, indicating an improper fraction.
Converting Improper Fractions to Mixed Numbers
An improper fraction, like 25/4, has a numerator larger than its denominator. This is often more intuitively understood as a mixed number, which combines a whole number and a proper fraction. Converting 25/4 to a mixed number involves dividing the numerator by the denominator:
25 ÷ 4 = 6 with a remainder of 1
This means we have 6 whole units and 1 part remaining out of the 4 parts that make up a whole. Therefore, 25/4 is equivalent to the mixed number 6 1/4.
This conversion is crucial for practical applications. Imagine you have 25 quarters. You can easily exchange these for 6 dollars (since 4 quarters make a dollar) with one quarter left over. This perfectly illustrates the concept of the mixed number representation of 25/4.
Visual Representation of 25/4
Visualizing fractions can significantly aid in comprehension. Consider representing 25/4 using a pictorial method:
Imagine four equal-sized squares. Each square represents one whole unit. To represent 25/4, we need six full squares (representing 6 whole units, 24/4) and one more square divided into four equal parts, with one of those parts shaded. This visual reinforces the mixed number equivalent: 6 1/4.
This visual approach is particularly helpful for younger learners or those who benefit from concrete representations of abstract concepts. The ability to visualize fractions is a key skill for developing a strong foundational understanding of fractions and their application.
Decimal Representation of 25/4
Another important representation of 25/4 is its decimal equivalent. To convert a fraction to a decimal, you simply divide the numerator by the denominator:
25 ÷ 4 = 6.25
Therefore, 25/4 is equal to 6.25. This decimal representation is frequently used in calculations and real-world applications where precision is required, such as measurements or financial calculations.
Practical Applications of 25/4
The fraction 25/4, and its various representations, finds application in various real-world scenarios. For example:
- Measurement: If you're measuring a length and find it to be 25/4 inches, you know it's 6.25 inches long.
- Finance: Imagine you're splitting a $25 bill among four friends. Each person would receive $6.25.
- Baking: A recipe might call for 25/4 cups of flour. This is equivalent to 6 1/4 cups.
- Construction: Measurements in construction often involve fractions, and understanding conversions is crucial for accuracy and efficiency.
These examples highlight the importance of understanding fractions and their conversions in various everyday contexts. The ability to fluently convert between fractions, mixed numbers, and decimals is essential for solving problems across multiple disciplines.
Adding, Subtracting, Multiplying, and Dividing Fractions Involving 25/4
Performing arithmetic operations with fractions like 25/4 requires understanding the rules of fraction manipulation. Let's explore each operation:
-
Addition/Subtraction: To add or subtract fractions, you must have a common denominator. For example, to add 25/4 and 1/2, we first find a common denominator (4), then convert 1/2 to 2/4. The sum is then (25/4) + (2/4) = 27/4 or 6 ¾. Subtraction follows a similar process.
-
Multiplication: Multiplying fractions is straightforward. Multiply the numerators together and then the denominators: (25/4) x (2/3) = 50/12. This can then be simplified to 25/6 or 4 1/6.
-
Division: To divide fractions, you invert the second fraction and multiply: (25/4) ÷ (1/2) = (25/4) x (2/1) = 50/4 = 25/2 or 12 ½.
Advanced Concepts: Ratios and Proportions involving 25/4
Fractions are intrinsically linked to ratios and proportions. A ratio expresses the relationship between two quantities. For example, 25/4 could represent a ratio of 25 to 4. Proportions involve setting two ratios equal to each other to solve for an unknown quantity.
Understanding ratios and proportions is crucial in fields like scaling, mixing ingredients (in cooking or chemistry), and map reading. The fraction 25/4 serves as a simple yet illustrative example of how these concepts intertwine with fractional understanding.
Error Analysis and Common Mistakes with 25/4
Several common mistakes can arise when working with fractions like 25/4:
- Incorrect Conversion to Mixed Numbers: Failing to correctly divide the numerator by the denominator and obtain the whole number and remainder can lead to inaccurate conversions.
- Improper Simplification: Not simplifying the resulting fraction to its lowest terms can make further calculations more complex.
- Errors in Arithmetic Operations: Mistakes in adding, subtracting, multiplying, or dividing fractions can stem from a lack of understanding of the basic rules.
- Misunderstanding Decimal Conversions: Incorrectly dividing the numerator by the denominator to obtain the decimal representation can lead to errors in calculations.
Frequently Asked Questions (FAQ)
Q: What is 25/4 as a percentage?
A: To convert a fraction to a percentage, first convert it to a decimal (6.25), then multiply by 100: 6.25 x 100 = 625%.
Q: How do I simplify 25/4?
A: 25/4 is already in its simplest form as an improper fraction. The simplified mixed number is 6 ¼.
Q: Can 25/4 be expressed as a recurring decimal?
A: No, 25/4 is a terminating decimal (6.25). Recurring decimals occur when the division results in a non-terminating, repeating pattern.
Q: What are some real-world examples where I might encounter 25/4?
A: You might encounter it in various measurements, financial calculations, recipe ingredients, or even in statistical data analysis.
Conclusion: Mastering the Fraction 25/4 and Beyond
Understanding the fraction 25/4 extends beyond simple calculation. It’s about grasping the fundamental concepts of fractions, their diverse representations (mixed numbers, decimals), and their application in various contexts. By mastering these skills, you build a solid foundation for more advanced mathematical concepts and improve your ability to solve real-world problems. This comprehensive guide has equipped you with the tools and knowledge to not only understand 25/4 but also to approach any fraction with confidence and clarity. Remember to practice regularly, utilize visual aids when needed, and don't hesitate to revisit the concepts to reinforce your learning. The journey of mastering mathematics is continuous, and every step, like understanding 25/4, brings you closer to a deeper appreciation of numbers and their power.
Latest Posts
Latest Posts
-
75 Of 160
Sep 17, 2025
-
100 Divided 15
Sep 17, 2025
-
C Est Magnifique Translation
Sep 17, 2025
-
80 Of 56
Sep 17, 2025
-
6 9kg In Lbs
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.