25 Of 1400
stanleys
Sep 17, 2025 · 5 min read
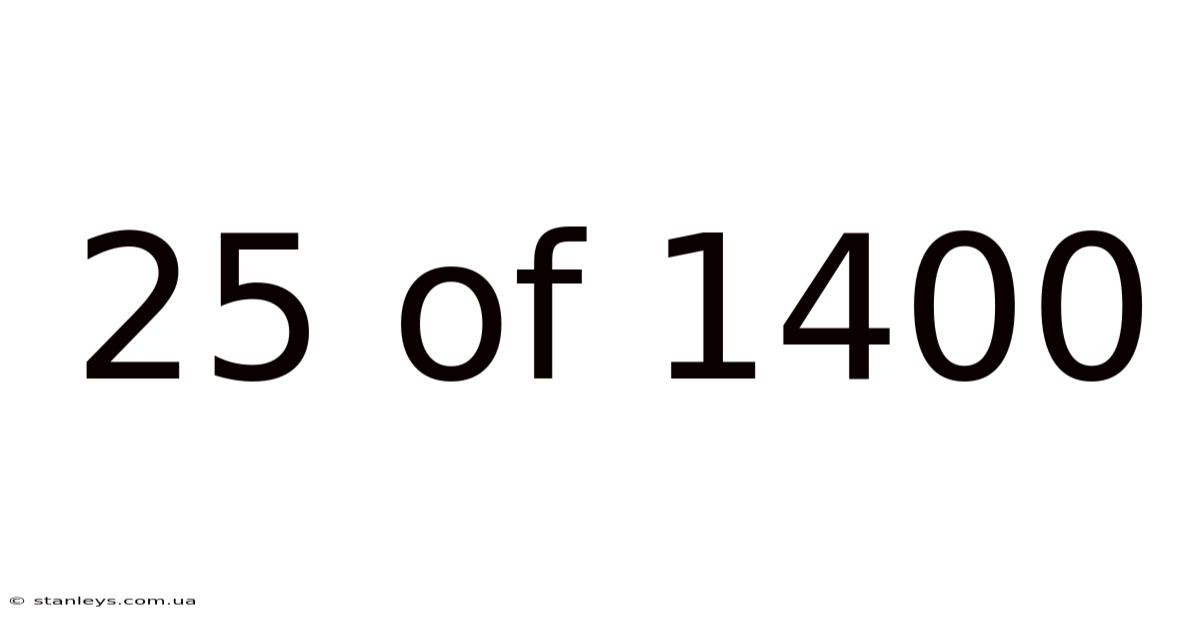
Table of Contents
Understanding the Significance of "25 of 1400": A Deep Dive into Ratios, Proportions, and Percentages
The seemingly simple phrase "25 of 1400" represents a fundamental concept in mathematics: ratios, proportions, and percentages. Understanding this seemingly simple statement unlocks a world of applications across various fields, from everyday calculations to complex scientific analyses. This article will explore the multifaceted meaning of "25 of 1400," examining its numerical representation, practical applications, and the broader mathematical principles it exemplifies.
What does "25 of 1400" mean?
At its core, "25 of 1400" indicates a part-to-whole relationship. It signifies that 25 is a portion of a larger whole, 1400. This relationship can be expressed in several ways:
-
Ratio: The ratio is 25:1400, or simplified to 1:56. This shows that for every one part, there are 56 parts in the whole.
-
Fraction: The fraction is 25/1400, which also simplifies to 1/56. This represents 25 as a fraction of the total 1400.
-
Percentage: To express it as a percentage, we calculate (25/1400) * 100% ≈ 1.79%. This means 25 represents approximately 1.79% of 1400.
Practical Applications: Real-World Scenarios
The concept of "25 of 1400" finds relevance in numerous real-world scenarios. Let's consider a few examples:
-
Survey Results: Imagine a survey of 1400 people, where 25 respondents chose a particular option. The ratio, fraction, and percentage calculations help analyze the popularity of that option within the larger sample. This data can be crucial for market research, opinion polls, or academic studies.
-
Inventory Management: A warehouse might have 1400 units of a particular product, with 25 units being damaged or defective. Determining the percentage of damaged goods is crucial for inventory control, quality assurance, and financial planning.
-
Statistical Analysis: In scientific research or statistical analysis, "25 of 1400" could represent a sample size. Researchers might analyze 25 data points from a larger dataset of 1400 to draw inferences about the entire population. Understanding the percentage of the sample relative to the whole is crucial for determining the statistical significance of findings.
-
Financial Calculations: Consider a portfolio of 1400 investments, with 25 showing significant losses. Calculating the percentage of underperforming investments helps in risk assessment and portfolio management.
-
Quality Control: In manufacturing, 25 out of 1400 products might be deemed defective during quality control checks. The percentage of defective items helps determine production efficiency and quality standards.
Mathematical Principles Involved
Understanding "25 of 1400" necessitates grasping core mathematical principles:
-
Ratios: A ratio compares two or more quantities. In our example, the ratio 25:1400 compares the number of parts to the whole. Ratios can be simplified by dividing both numbers by their greatest common divisor (GCD). In this case, the GCD of 25 and 1400 is 25, leading to the simplified ratio of 1:56.
-
Proportions: A proportion is a statement that two ratios are equal. For instance, we could set up a proportion to solve for an unknown value. If x represents a percentage, the proportion would be: 25/1400 = x/100. Solving for x gives us the percentage value.
-
Percentages: A percentage is a ratio expressed as a fraction of 100. Converting a fraction to a percentage involves multiplying the fraction by 100%. In our example, (25/1400) * 100% ≈ 1.79%.
-
Simplification: Simplifying fractions and ratios makes calculations easier and improves understanding. The simplified fraction 1/56 provides a clearer representation of the relationship between 25 and 1400 than the original fraction 25/1400.
Expanding the Concept: Beyond the Basics
The concept of "25 of 1400" extends beyond simple calculations. It forms the foundation for more complex statistical analyses:
-
Sampling: In statistics, researchers often use a sample from a larger population to draw conclusions about the entire population. Understanding the ratio between the sample size (25) and the population size (1400) is crucial for determining the reliability and accuracy of the conclusions. The larger the sample size relative to the population, generally, the more reliable the results.
-
Probability: The fraction 25/1400 can be interpreted as the probability of selecting a particular item from a set of 1400 items. This probability can be used to make predictions about future events.
-
Confidence Intervals: When estimating a population parameter based on a sample, statisticians often construct confidence intervals. The sample size (25) and the population size (1400) influence the width of the confidence interval – a smaller sample size generally leads to a wider confidence interval, reflecting greater uncertainty.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate the percentage from a ratio?
- A: To calculate the percentage from a ratio, express the ratio as a fraction, then multiply by 100%. For example, the ratio 25:1400 becomes the fraction 25/1400. Multiplying by 100% gives approximately 1.79%.
-
Q: What is the difference between a ratio and a proportion?
- A: A ratio compares two quantities, while a proportion states that two ratios are equal. A ratio is a comparison; a proportion is an equation.
-
Q: Why is it important to simplify fractions and ratios?
- A: Simplifying makes calculations easier and provides a clearer understanding of the relationship between the quantities. It makes it easier to visualize the proportion and interpret the results.
-
Q: How does sample size affect the reliability of statistical conclusions?
- A: A larger sample size generally leads to more reliable conclusions. A smaller sample size may be more prone to sampling error and bias.
-
Q: Can "25 of 1400" be used in different contexts?
- A: Absolutely! The concept applies broadly across diverse fields and situations where a part-to-whole relationship needs to be quantified and analyzed.
Conclusion
The seemingly simple phrase "25 of 1400" opens a window into a world of mathematical principles and practical applications. Understanding its representation as a ratio, fraction, and percentage allows us to analyze proportions, interpret data, and make informed decisions in various contexts. Whether in market research, inventory management, scientific studies, or financial analysis, mastering the calculation and interpretation of such relationships is essential for informed decision-making and effective problem-solving. The core concepts – ratios, proportions, and percentages – are fundamental building blocks for more complex mathematical and statistical analyses, highlighting the importance of a strong foundation in these basic mathematical concepts. The seemingly simple phrase holds far greater depth than initially apparent, underscoring the power of fundamental mathematical concepts to inform and shape our understanding of the world around us.
Latest Posts
Latest Posts
-
Cth Medical Abbreviation
Sep 17, 2025
-
32km To Miles
Sep 17, 2025
-
Charge Of Zn
Sep 17, 2025
-
7 1 9
Sep 17, 2025
-
10 Of 60
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 1400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.