24 Of 84
stanleys
Sep 21, 2025 · 5 min read
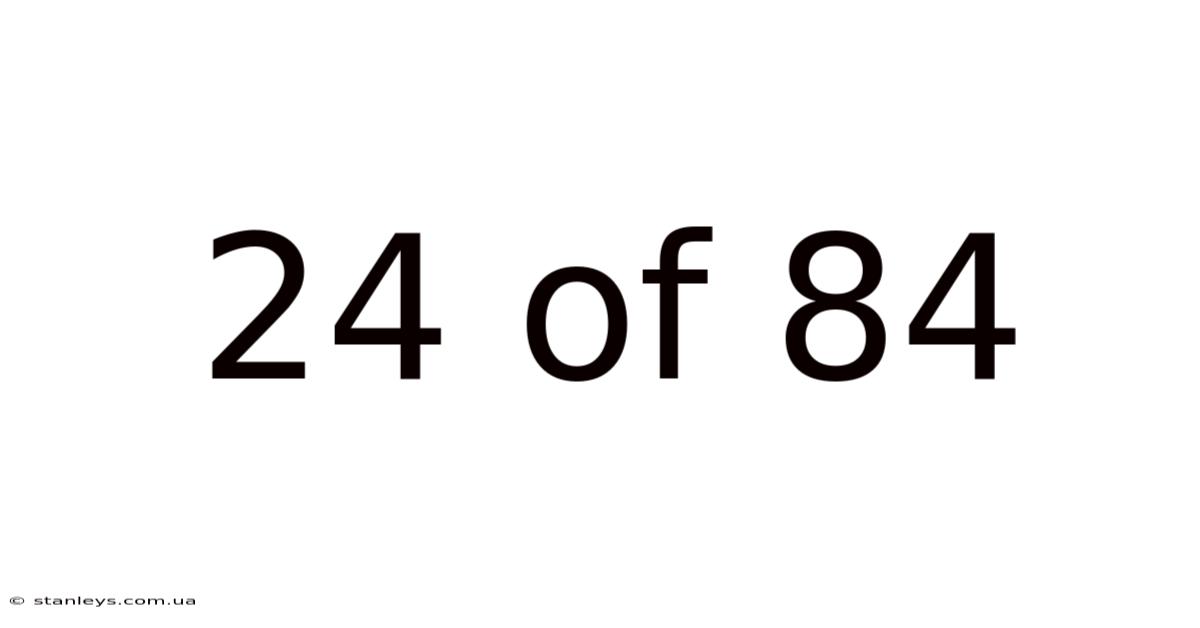
Table of Contents
Decoding the Enigma: Understanding the Significance of 24/84 and its Applications
The seemingly simple fraction 24/84 might appear insignificant at first glance. However, a deeper dive reveals its multifaceted nature, touching upon fundamental mathematical concepts and finding applications in diverse fields. This article will explore the meaning and significance of 24/84, delving into its simplification, percentage representation, ratio interpretation, and real-world applications. We will also address frequently asked questions about fractions and explore the broader context of rational numbers.
Introduction: Unveiling the Simplicity Within Complexity
The fraction 24/84 represents a part of a whole, a relationship between two numbers. Understanding this relationship forms the bedrock of many mathematical operations and real-world problem-solving. While seemingly straightforward, the fraction presents an opportunity to explore fundamental concepts such as simplification, equivalent fractions, and the conversion between fractions, decimals, and percentages. This exploration will not only enhance mathematical literacy but also provide a foundation for understanding more complex mathematical ideas.
Step-by-Step Simplification: Reducing to the Lowest Terms
The first step in understanding 24/84 is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (24) and the denominator (84). The GCD is the largest number that divides both 24 and 84 without leaving a remainder.
-
Finding the GCD: We can find the GCD using various methods, such as prime factorization or the Euclidean algorithm. Let's use prime factorization:
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
- 84 = 2 x 2 x 3 x 7 = 2² x 3 x 7
The common factors are 2² and 3. Therefore, the GCD is 2² x 3 = 12.
-
Dividing the Numerator and Denominator: We divide both the numerator and the denominator by the GCD (12):
- 24 ÷ 12 = 2
- 84 ÷ 12 = 7
Therefore, the simplified fraction is 2/7.
Understanding Equivalent Fractions: Exploring Different Representations
It's crucial to understand that 24/84 and 2/7 are equivalent fractions. They represent the same proportion or part of a whole. Many other fractions are also equivalent to 2/7, such as 4/14, 6/21, 8/28, and so on. These fractions are obtained by multiplying both the numerator and the denominator by the same number. Simplifying a fraction to its lowest terms, like we did with 24/84, makes it easier to work with and compare with other fractions.
Percentage Representation: Expressing the Fraction as a Percentage
To express 2/7 as a percentage, we need to convert the fraction to a decimal and then multiply by 100.
-
Converting to a Decimal: Divide the numerator (2) by the denominator (7): 2 ÷ 7 ≈ 0.2857
-
Multiplying by 100: 0.2857 x 100 ≈ 28.57%
Therefore, 24/84 is approximately 28.57%.
Ratio Interpretation: Understanding the Relationship Between Two Quantities
The fraction 24/84 can also be interpreted as a ratio. It represents the relationship between two quantities – 24 and 84. For example, if there are 24 red balls and 84 blue balls in a bag, the ratio of red balls to blue balls is 24:84, which simplifies to 2:7. This means that for every 2 red balls, there are 7 blue balls.
Real-World Applications: Examples of the Fraction in Practice
The fraction 24/84, or its simplified form 2/7, can find applications in various real-world scenarios. Here are a few examples:
-
Mixing Ingredients: Imagine a recipe requiring 2 cups of flour and 7 cups of water. The ratio of flour to water is 2:7, directly reflecting the simplified fraction.
-
Probability: If there are 2 favorable outcomes out of 7 possible outcomes in an event, the probability of the favorable event occurring is 2/7.
-
Scaling and Proportion: If a map has a scale where 2 cm represents 7 km, the ratio is 2:7. This allows for converting distances on the map to real-world distances.
-
Data Analysis: In statistical analysis, the fraction might represent a proportion of a sample possessing a certain characteristic.
Scientific Explanation: The Foundation in Number Theory
The mathematical operations involved in simplifying 24/84 and understanding its equivalent forms are rooted in number theory. The concept of the greatest common divisor (GCD) is fundamental to simplifying fractions and finding equivalent ratios. The ability to express a fraction as a percentage or decimal is crucial for various calculations and comparisons.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a fraction and a ratio? A: While often used interchangeably, a fraction represents a part of a whole, while a ratio represents the relationship between two quantities. However, both can be expressed in the form a/b.
-
Q: How do I convert a decimal to a fraction? A: To convert a decimal to a fraction, write the decimal as the numerator and place a power of 10 (10, 100, 1000, etc.) as the denominator, depending on the number of decimal places. Then, simplify the fraction to its lowest terms.
-
Q: What are rational numbers? A: Rational numbers are numbers that can be expressed as a fraction a/b, where 'a' and 'b' are integers, and 'b' is not equal to zero. 24/84 is a rational number.
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a more concise and efficient representation of the proportion.
Conclusion: A Deeper Understanding of Basic Mathematics
The seemingly simple fraction 24/84 offers a rich opportunity to explore fundamental mathematical concepts. Through simplification, we arrive at the equivalent fraction 2/7, allowing for easier manipulation and comparison. Understanding its percentage representation, ratio interpretation, and diverse applications highlights the practical relevance of even basic mathematical principles. This comprehensive exploration emphasizes the importance of foundational mathematical knowledge in various aspects of life, paving the way for tackling more advanced mathematical challenges. From recipes to probability, maps to data analysis, the principles demonstrated by 24/84 permeate numerous areas, highlighting the enduring relevance of this seemingly simple fraction. The journey from 24/84 to 2/7 is a microcosm of the power of simplification and understanding in mathematics, enriching our comprehension of numbers and their relationships in the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 24 Of 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.