21 X 12
stanleys
Sep 14, 2025 · 6 min read
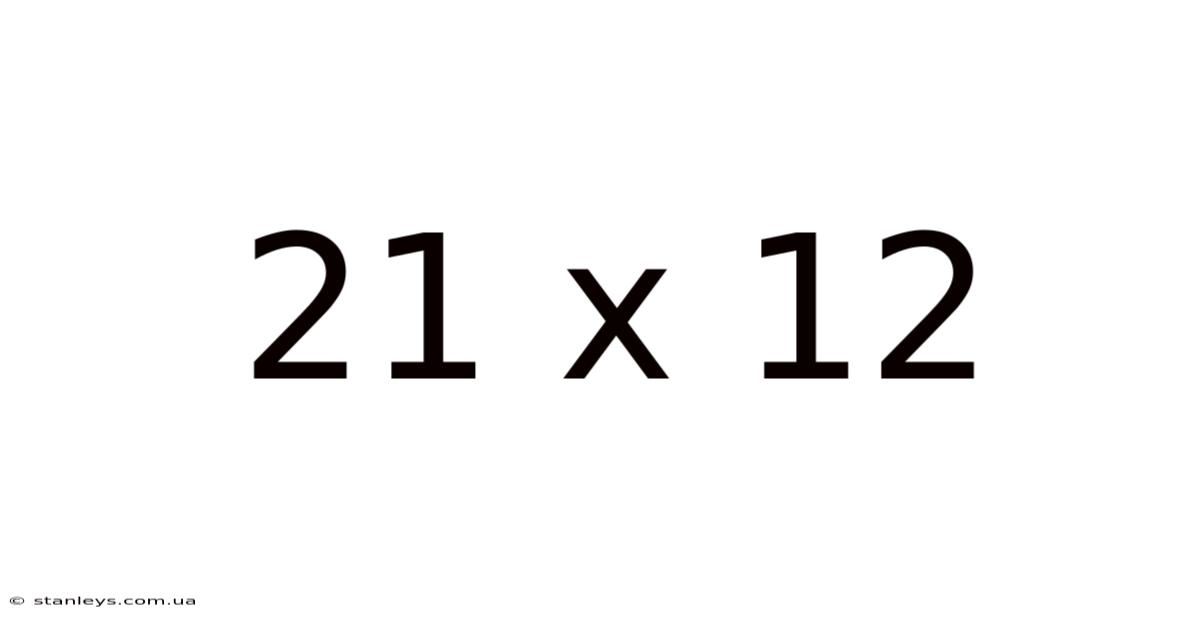
Table of Contents
Decoding 21 x 12: A Deep Dive into Multiplication, Its Applications, and Beyond
The seemingly simple multiplication problem, 21 x 12, opens a door to a vast world of mathematical concepts and practical applications. This article will not only solve this specific equation but also explore the underlying principles of multiplication, delve into its various methods, and showcase its relevance in diverse real-world scenarios. We'll journey from basic arithmetic to advanced applications, ensuring a comprehensive understanding for readers of all levels.
Introduction: Understanding the Fundamentals
Multiplication, at its core, is repeated addition. 21 x 12 simply means adding 21 twelve times, or adding 12 twenty-one times. While this approach works, it's inefficient for larger numbers. This is where understanding the structure of multiplication and employing efficient methods becomes crucial. This equation, seemingly simple, offers a fantastic platform to explore these efficient strategies and their broader mathematical implications. We'll cover various methods, from the traditional column method to the distributive property, and discuss the advantages and disadvantages of each. The goal is to not only solve 21 x 12 but to equip you with the tools to tackle any multiplication problem with confidence and understanding.
Methods for Solving 21 x 12
Several approaches can solve 21 x 12. Let's examine a few:
- The Traditional Column Method: This is the most common method taught in schools.
21
x 12
----
42 (21 x 2)
210 (21 x 10)
----
252
This method involves multiplying 21 by each digit of 12 separately (2 and 10) and then adding the results. It leverages the concept of place value, where the position of a digit determines its value (ones, tens, hundreds, etc.).
- Distributive Property: This method utilizes the distributive property of multiplication over addition: a(b + c) = ab + ac. We can rewrite 12 as (10 + 2), then distribute:
21 x (10 + 2) = (21 x 10) + (21 x 2) = 210 + 42 = 252
This method highlights the underlying structure of multiplication and can be particularly helpful when dealing with larger numbers or expressions.
- The Lattice Method: Although less commonly used, the lattice method provides a visual representation of the multiplication process. It's particularly useful for beginners to grasp the concept of place value and partial products.
(Diagram would be included here showing the lattice method visually solving 21 x 12, explaining each step).
- Mental Math Techniques: With practice, you can develop mental math techniques to solve this equation quickly. For instance, you could break down 21 into (20 + 1) and then distribute: (20 + 1) x 12 = (20 x 12) + (1 x 12) = 240 + 12 = 252.
Regardless of the method employed, the answer remains the same: 252.
Beyond the Calculation: Exploring Applications of Multiplication
The seemingly simple calculation of 21 x 12 holds significant relevance across various fields:
-
Everyday Life: Imagine you're buying 21 packs of cookies, each containing 12 cookies. To find the total number of cookies, you would use multiplication: 21 x 12 = 252 cookies. This illustrates the practical application of multiplication in everyday purchasing and inventory management.
-
Geometry and Area Calculation: If you have a rectangle with a length of 21 units and a width of 12 units, the area of that rectangle is found by multiplying the length and width: 21 x 12 = 252 square units. This concept extends to calculating the area of more complex shapes, leading to applications in architecture, engineering, and design.
-
Finance and Business: Multiplication is fundamental in finance. Calculating total earnings, profits, losses, interest calculations, and much more involves multiplication. For instance, if a company makes a profit of $21 per item and sells 12 items, the total profit is 21 x 12 = $252.
-
Science and Engineering: Multiplication plays a crucial role in various scientific and engineering calculations, including physics (force, energy, and work calculations), chemistry (mole calculations), and engineering (structural analysis and design).
-
Computer Science: Multiplication is a fundamental operation in computer programming and algorithms. It's used in various computations, from simple arithmetic to complex simulations and data processing.
Expanding the Understanding: Factors and Multiples
Understanding the concept of factors and multiples adds another layer to comprehending 21 x 12.
-
Factors: The factors of a number are the numbers that divide it evenly without leaving a remainder. The factors of 252 include 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, and 252.
-
Multiples: Multiples of a number are the numbers obtained by multiplying that number by any integer. 252 is a multiple of 21 and 12. Understanding factors and multiples helps in simplifying calculations and identifying patterns in numbers.
Advanced Concepts: Prime Factorization and Exponents
Let's delve further into more advanced mathematical concepts related to 21 x 12.
-
Prime Factorization: Breaking down a number into its prime factors (numbers divisible only by 1 and themselves) provides a deeper understanding of its structure. The prime factorization of 252 is 2² x 3² x 7. This means 252 can be expressed as (2 x 2) x (3 x 3) x 7. Prime factorization is fundamental in many areas of mathematics, including number theory and cryptography.
-
Exponents: Exponents represent repeated multiplication. In the prime factorization of 252 (2² x 3² x 7), the exponents (2 and 2) indicate repeated multiplication: 2² = 2 x 2 = 4 and 3² = 3 x 3 = 9. Exponents simplify the representation of large numbers and are crucial in algebraic manipulation and calculus.
Frequently Asked Questions (FAQ)
-
Q: What are the different ways to represent 21 x 12?
- A: Besides the standard form, it can be represented using the distributive property, as (20+1) x 12, or as repeated addition (adding 21 twelve times, or 12 twenty-one times).
-
Q: Is there a quickest way to solve 21 x 12 mentally?
- A: With practice, using the distributive property, breaking 21 into (20 + 1) and multiplying each part by 12 separately, then adding the results, becomes quite efficient.
-
Q: How does this calculation relate to other mathematical concepts?
- A: This simple calculation is intertwined with numerous mathematical concepts, including factors, multiples, prime factorization, the distributive property, and area calculation, all fundamental to further mathematical studies.
-
Q: Why is understanding multiplication important?
- A: Multiplication is a cornerstone of mathematics and is crucial for understanding and solving problems in various fields, from daily finances to complex scientific calculations.
Conclusion: A Deeper Appreciation for Multiplication
The seemingly straightforward problem of 21 x 12 offers a rich opportunity to explore the fascinating world of mathematics. From basic arithmetic operations to advanced concepts like prime factorization and exponents, this single equation reveals the interconnectedness of mathematical principles. By understanding the various methods of solving multiplication problems and appreciating their applications in real-world scenarios, we gain a deeper understanding of the power and relevance of mathematics in our daily lives. The seemingly simple act of multiplying 21 by 12 underscores the beauty and utility of this fundamental mathematical operation, demonstrating its profound impact across diverse fields and levels of mathematical complexity. It's not just about the answer (252); it's about the journey of understanding the underlying principles and their far-reaching consequences.
Latest Posts
Latest Posts
-
17cms In Inches
Sep 14, 2025
-
35pounds To Kg
Sep 14, 2025
-
70 Of 65
Sep 14, 2025
-
Lee Friedlander Photographer
Sep 14, 2025
-
300pounds In Kg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 21 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.