20 Of 1200
stanleys
Sep 06, 2025 · 6 min read
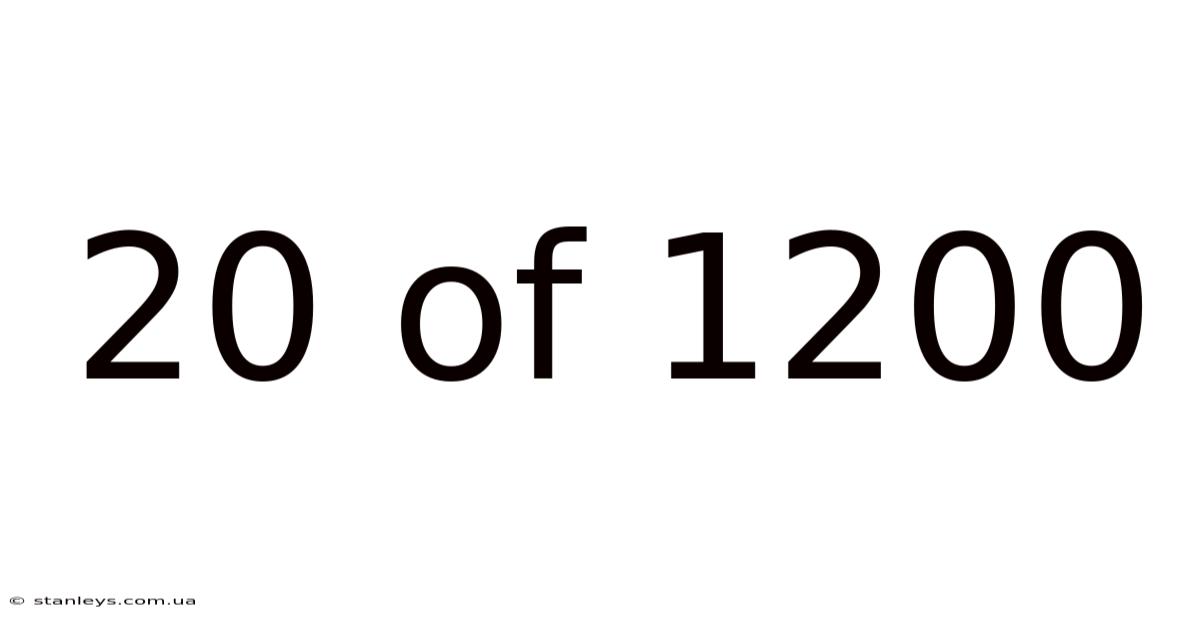
Table of Contents
Decoding the Fraction: Understanding 20 out of 1200
Understanding fractions can feel daunting, especially when dealing with larger numbers like "20 out of 1200". This seemingly simple phrase represents a core concept in mathematics crucial for various applications, from everyday calculations to advanced statistical analysis. This article will break down the meaning of 20 out of 1200, exploring its various representations, calculations, and practical implications. We'll delve into how to express this fraction in its simplest form, calculate percentages, and understand its significance within different contexts. By the end, you'll not only understand this specific fraction but also gain a stronger grasp of fractional concepts in general.
Understanding the Basics: What does "20 out of 1200" mean?
The phrase "20 out of 1200" represents a ratio. It signifies that there are 20 parts of a whole comprising 1200 parts. Think of it like this: if you have 1200 marbles, and 20 of them are red, then "20 out of 1200" describes the proportion of red marbles. This ratio can be expressed in several ways, each with its own advantages.
Expressing the Ratio: Fractions, Decimals, and Percentages
There are three primary ways to express the ratio "20 out of 1200":
-
Fraction: The most direct representation is a fraction: 20/1200. This clearly shows the part (20) over the whole (1200).
-
Decimal: To convert the fraction to a decimal, we divide the numerator (20) by the denominator (1200): 20 ÷ 1200 = 0.016666... This decimal representation provides a precise numerical value. The repeating '6' indicates that the decimal is non-terminating.
-
Percentage: Percentages offer a readily understandable representation of proportions. To convert the fraction to a percentage, we multiply the decimal by 100: 0.016666... × 100 ≈ 1.67%. This means that 20 out of 1200 represents approximately 1.67% of the whole.
Simplifying the Fraction: Finding the Lowest Terms
The fraction 20/1200 can be simplified to its lowest terms by finding the greatest common divisor (GCD) of 20 and 1200. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. In this case, the GCD of 20 and 1200 is 20.
Dividing both the numerator and the denominator by 20, we get:
20 ÷ 20 = 1 1200 ÷ 20 = 60
Therefore, the simplified fraction is 1/60. This simplified form is easier to work with and provides a clearer understanding of the ratio's magnitude. Both 20/1200 and 1/60 represent the same proportion, just expressed differently.
Practical Applications: Real-World Examples
The concept of "20 out of 1200" has numerous real-world applications. Let's look at a few examples:
-
Quality Control: Imagine a factory producing 1200 widgets. If 20 widgets are found to be defective, the fraction 20/1200 (or 1/60) represents the defect rate. This information is crucial for improving production processes.
-
Surveys and Statistics: If a survey of 1200 people reveals that 20 support a particular policy, the fraction 20/1200 (or 1.67%) shows the level of support for that policy within the sample population.
-
Financial Analysis: In finance, this concept could represent a small portion of a larger investment portfolio. Understanding this proportion helps in assessing the overall risk and return of the investment.
-
Academic Performance: If a student answers 20 questions correctly out of a total of 1200 questions across various exams throughout the year, this fraction could be used to assess their overall academic performance. This wouldn’t be a very good result, demonstrating a need for improvement.
-
Environmental Studies: If 20 out of 1200 tested samples of water contain a particular pollutant, this represents a significant environmental concern that requires further investigation and remediation.
Understanding Percentage Change: A Deeper Dive
While expressing "20 out of 1200" as a percentage (approximately 1.67%) provides a convenient representation, understanding percentage change requires a slightly different approach. Suppose, for instance, the initial number was 1200, and it decreased to 1180. The decrease is 20. To calculate the percentage change, we use the following formula:
Percentage Change = [(New Value - Old Value) / Old Value] × 100
In this case:
Percentage Change = [(1180 - 1200) / 1200] × 100 = -1.67%
This indicates a decrease of approximately 1.67%. It's important to distinguish between expressing a proportion (like 20 out of 1200) and calculating a percentage change.
Calculating Proportions with Different Numbers: Applying the Concepts
The principles involved in understanding "20 out of 1200" are applicable to any ratio. Let's consider a different example: "35 out of 700".
-
Fraction: 35/700
-
Simplified Fraction: Dividing both numerator and denominator by 35, we get 1/20.
-
Decimal: 35 ÷ 700 = 0.05
-
Percentage: 0.05 × 100 = 5%
Notice that even though the numbers are different, the process of converting to a simplified fraction, decimal, and percentage remains the same.
Further Exploration: Advanced Applications
The concept of ratios and proportions extends far beyond these basic examples. In advanced mathematics, statistics, and other fields, understanding these fundamental concepts is critical. Applications include:
-
Probability: Calculating the probability of events.
-
Statistical Inference: Making inferences about populations based on sample data.
-
Financial Modeling: Creating models to predict future financial performance.
-
Engineering and Physics: Solving problems involving ratios and proportions in various physical systems.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to simplify a fraction?
A: The easiest way is to find the greatest common divisor (GCD) of the numerator and denominator and divide both by it. Many calculators and online tools can help find the GCD.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It provides a clearer representation of the proportion and facilitates further calculations.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators can perform this conversion. Simply divide the numerator by the denominator, then multiply by 100.
Q: What if the numbers are very large?
A: Even with very large numbers, the process of converting to a fraction, decimal, or percentage remains the same. Using a calculator or computer software can be helpful for larger numbers to ensure accuracy.
Conclusion: Mastering Fractions for a Better Understanding of the World
Understanding the meaning and implications of "20 out of 1200," as well as the broader principles of ratios and proportions, is a foundational skill with significant practical value. By mastering these concepts, you'll not only improve your mathematical abilities but also gain a more nuanced understanding of data, statistics, and the world around you. This knowledge equips you to analyze information more effectively and make more informed decisions in various contexts. Remember, the seemingly simple act of understanding a fraction like 20/1200 opens doors to a deeper comprehension of numerical relationships and their practical significance across diverse fields.
Latest Posts
Latest Posts
-
Grains In Gramm
Sep 12, 2025
-
91km In Miles
Sep 12, 2025
-
93 3kg In Stone
Sep 12, 2025
-
93 9kg In Stone
Sep 12, 2025
-
Lb En Newton
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.