2.6 Cos 12
stanleys
Sep 21, 2025 · 7 min read
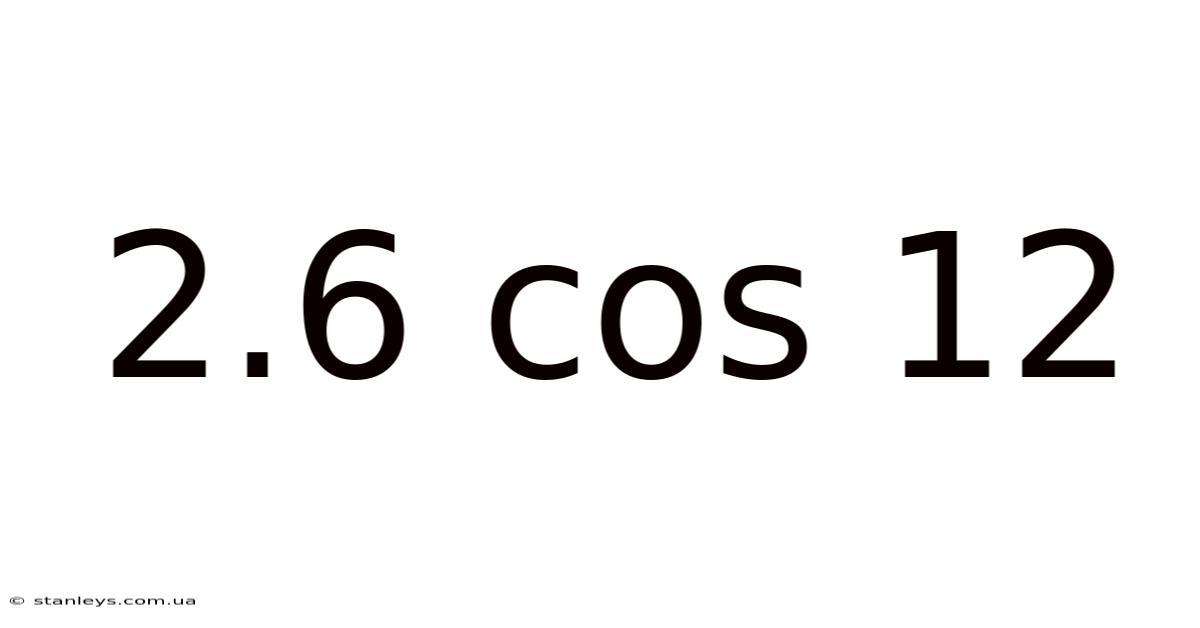
Table of Contents
Decoding 2.6 cos 12: A Deep Dive into Trigonometry and its Applications
This article explores the mathematical expression "2.6 cos 12," breaking down its components, explaining the underlying principles of trigonometry, and demonstrating its practical applications across various fields. We'll delve into the concepts of cosine, angles (in degrees and radians), and how these elements combine to yield a numerical result. This exploration is designed to be accessible to a broad audience, from high school students to anyone curious about the practical use of mathematics. Understanding "2.6 cos 12" requires a grasp of fundamental trigonometry, which we will carefully unpack.
Understanding the Components: Numbers and Angles
The expression "2.6 cos 12" consists of three key components:
-
2.6: This is a constant coefficient, a simple numerical value that scales the result of the cosine function. It's a multiplier that will stretch or compress the final answer.
-
cos: This is the trigonometric function cosine. The cosine of an angle in a right-angled triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. In a unit circle context (a circle with radius 1), the cosine of an angle represents the x-coordinate of the point where the angle intersects the circle.
-
12: This is the angle, measured in degrees. It's crucial to understand that trigonometric functions operate on angles. The angle 12 degrees is a relatively small angle, and its cosine will be a positive value close to 1.
Calculating the Result: Putting it All Together
To calculate the value of "2.6 cos 12," we need a calculator capable of handling trigonometric functions (most scientific calculators and online calculators have this capability). The steps are straightforward:
-
Set your calculator to degrees mode: Ensure your calculator is set to use degrees as the unit for angles. Radians are another common unit for angles, and using the wrong unit will give an entirely different result.
-
Find the cosine of 12 degrees: Enter "cos 12" into your calculator. You should get a value close to 0.9781. This is the cosine of 12 degrees.
-
Multiply by the coefficient: Multiply the result from step 2 by 2.6. This gives you the final answer: 2.6 * 0.9781 ≈ 2.547.
Therefore, 2.6 cos 12 ≈ 2.547. Note that this is an approximation; the precise value has more decimal places.
Trigonometric Functions: A Deeper Dive
Trigonometry is a branch of mathematics that studies the relationships between angles and sides of triangles. The three primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan). These functions are defined for angles in both right-angled triangles and within the context of the unit circle.
-
Sine (sin): In a right-angled triangle, the sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In the unit circle, it represents the y-coordinate of the point where the angle intersects the circle.
-
Cosine (cos): As previously explained, the cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse in a right-angled triangle. In the unit circle, it's the x-coordinate.
-
Tangent (tan): The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side. In the unit circle, it's the ratio of the y-coordinate to the x-coordinate.
These functions are periodic, meaning their values repeat at regular intervals. The period for sine and cosine is 360 degrees (or 2π radians). The tangent function has a period of 180 degrees (or π radians).
Angles: Degrees and Radians
Angles can be measured in degrees or radians. Degrees are a more familiar unit, with a full circle comprising 360 degrees. Radians are a unit based on the radius of a circle. One radian is the angle subtended at the center of a circle by an arc equal in length to the radius. There are 2π radians in a full circle (approximately 6.28 radians). Converting between degrees and radians involves the relationship:
- Radians = Degrees * (π/180)
- Degrees = Radians * (180/π)
It's essential to ensure your calculator is in the correct mode (degrees or radians) when performing trigonometric calculations.
Applications of Trigonometry: Beyond the Classroom
Trigonometry isn't just an abstract mathematical concept; it has numerous practical applications across diverse fields:
-
Engineering and Physics: Trigonometry is fundamental to engineering and physics, used in calculations involving forces, vectors, motion, and wave phenomena. Examples include structural analysis, projectile motion, and the analysis of electrical circuits. The expression "2.6 cos 12" could represent a component of a force vector, for instance.
-
Surveying and Navigation: Surveyors use trigonometry to determine distances and elevations, while navigators use it for calculations involving position, distance, and direction. Global Positioning Systems (GPS) rely heavily on trigonometric calculations.
-
Computer Graphics and Game Development: Trigonometry is crucial for creating realistic graphics and animations in computer games and other applications. It's used to model rotations, transformations, and perspective.
-
Astronomy: Trigonometric functions are essential for calculating distances and positions of celestial bodies.
-
Signal Processing: Trigonometric functions are used extensively in the analysis and processing of signals, such as sound waves and radio waves.
-
Medicine: Medical imaging techniques, such as ultrasound and X-ray, rely on trigonometric calculations.
Further Exploration and Advanced Concepts
While we've covered the basics of "2.6 cos 12," trigonometry encompasses many more advanced concepts. These include:
-
Trigonometric Identities: These are equations that are true for all values of the variables involved. They are useful for simplifying expressions and solving trigonometric equations.
-
Inverse Trigonometric Functions: These functions (arcsin, arccos, arctan) find the angle whose sine, cosine, or tangent is a given value.
-
Trigonometric Equations: These involve solving for unknown angles in equations containing trigonometric functions.
-
Hyperbolic Functions: These are similar to trigonometric functions but are defined using hyperbolic curves rather than circles.
-
Complex Numbers and Trigonometry: Trigonometry extends to the realm of complex numbers, creating connections between these seemingly disparate areas of mathematics.
Frequently Asked Questions (FAQ)
Q: What if the angle was given in radians instead of degrees?
A: If the angle was given in radians, you would need to ensure your calculator is set to radian mode before calculating the cosine. Remember to convert the radians to degrees if needed using the formula mentioned earlier.
Q: Why is the coefficient 2.6 important?
A: The coefficient 2.6 scales the result of the cosine function. It stretches or compresses the final answer. Without it, the result would simply be the cosine of 12 degrees.
Q: Are there other ways to represent the angle?
A: Yes, angles can also be represented in radians or using other units.
Q: Can this calculation be done without a calculator?
A: For simple angles like 0, 30, 45, 60, and 90 degrees, the cosine values can be memorized. However, for an angle like 12 degrees, a calculator is necessary for an accurate result.
Q: What are the real-world applications of this specific calculation (2.6 cos 12)?
A: The specific application depends on the context. It could represent a component of a force vector, a displacement, an amplitude of a wave, or various other quantities in engineering, physics, or other fields.
Conclusion
Understanding "2.6 cos 12" requires a foundational knowledge of trigonometry, including the concept of cosine, the measurement of angles in degrees, and the use of calculators to evaluate trigonometric functions. While the calculation itself is straightforward, its implications are far-reaching, with applications across multiple scientific and engineering disciplines. This article has aimed to provide a clear and comprehensive explanation, emphasizing both the calculation and the broader context of trigonometry, encouraging further exploration of this crucial mathematical field. The versatility and importance of trigonometry continue to solidify its role as a cornerstone of many advanced fields, proving its value extends far beyond theoretical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2.6 Cos 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.