2/5 Of 60
stanleys
Sep 11, 2025 · 6 min read
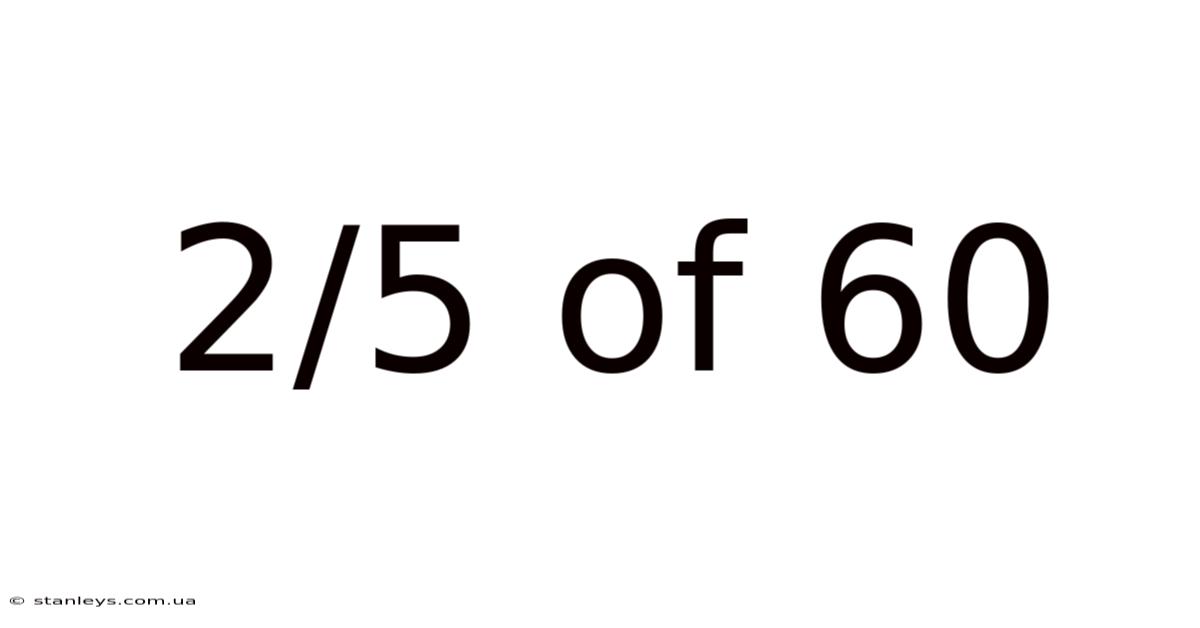
Table of Contents
Decoding 2/5 of 60: A Comprehensive Guide to Fractions and Their Applications
Finding 2/5 of 60 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper comprehension of fractions, their practical applications, and their importance in various fields. This article will delve into the intricacies of solving this problem, explore the underlying mathematical concepts, and demonstrate how this type of calculation is relevant in everyday life, from cooking and budgeting to more complex scenarios in engineering and finance.
Understanding Fractions: A Foundation for Calculation
Before tackling 2/5 of 60, let's establish a solid understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we're considering 2 out of 5 equal parts of a whole.
Several key concepts are crucial when working with fractions:
-
Equivalent Fractions: These are fractions that represent the same value, even though they look different. For example, 1/2 is equivalent to 2/4, 3/6, and so on. Understanding equivalent fractions is crucial for simplifying calculations and comparing fractions.
-
Simplifying Fractions: This involves reducing a fraction to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). For instance, 4/8 can be simplified to 1/2 by dividing both 4 and 8 by 4.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾). It's often useful to convert between these forms depending on the context of the problem.
-
Operations with Fractions: Just like whole numbers, fractions can be added, subtracted, multiplied, and divided. These operations involve specific rules that must be followed to obtain accurate results.
Calculating 2/5 of 60: Step-by-Step Solution
Now, let's address the core problem: finding 2/5 of 60. There are two primary methods to solve this:
Method 1: Multiplication
This is the most straightforward method. "Of" in mathematics usually implies multiplication. Therefore, finding 2/5 of 60 is equivalent to multiplying 2/5 by 60:
(2/5) x 60 = (2 x 60) / 5 = 120 / 5 = 24
Therefore, 2/5 of 60 is 24.
Method 2: Finding One-Fifth and Doubling
This method involves breaking down the problem into smaller, more manageable steps. First, we find 1/5 of 60:
60 / 5 = 12
Since we want 2/5, we simply double the result:
12 x 2 = 24
Again, we arrive at the answer: 24.
Real-World Applications of Fraction Calculations
The seemingly simple calculation of 2/5 of 60 has far-reaching applications in numerous real-world scenarios. Here are just a few examples:
-
Cooking and Baking: Recipes often use fractions to specify ingredient quantities. If a recipe calls for 2/5 of a cup of sugar, understanding how to calculate this fraction is essential for accurate measurement.
-
Shopping and Budgeting: Sales and discounts are frequently expressed as fractions. For example, a 2/5 discount on a $60 item means a saving of $24 (as we calculated above). Understanding fractions helps consumers make informed purchasing decisions and manage their budgets effectively.
-
Engineering and Construction: Fractions are fundamental in engineering and construction, used in measurements, scaling blueprints, and calculating material quantities. Accuracy in these calculations is crucial for the structural integrity and functionality of buildings and other structures.
-
Finance and Investments: Fractions are used extensively in financial calculations, including interest rates, stock valuations, and profit margins. Understanding fractional calculations is essential for making sound financial decisions.
-
Data Analysis and Statistics: Fractions and percentages (which are essentially fractions with a denominator of 100) are essential tools in data analysis and statistics. They help to represent proportions, probabilities, and relationships between different variables.
Extending the Concept: Working with More Complex Fractions
While 2/5 of 60 is a relatively straightforward calculation, the principles involved can be applied to more complex problems involving different fractions and operations. Consider these scenarios:
-
Adding and Subtracting Fractions: Imagine needing to determine the total quantity of ingredients when combining fractions of different items in a recipe. This would involve adding or subtracting fractions with unlike denominators, requiring finding a common denominator before performing the operation.
-
Multiplying Fractions with Whole Numbers and other Fractions: Scaling a recipe up or down requires multiplying fractions by whole numbers or other fractions. This involves multiplying the numerators together and the denominators together, then simplifying the resulting fraction if possible.
-
Dividing Fractions: Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying. This operation might be needed when calculating ratios or proportions.
Mastering these fundamental operations lays the groundwork for solving more complex problems involving percentages, ratios, and proportions – concepts that are crucial in numerous academic and professional fields.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 2/5?
A: 2/5 is already in its simplest form. The numerator (2) and denominator (5) have no common factors other than 1.
Q: How can I convert 2/5 to a decimal?
A: To convert a fraction to a decimal, divide the numerator by the denominator: 2 ÷ 5 = 0.4
Q: How can I convert 2/5 to a percentage?
A: To convert a fraction to a percentage, first convert it to a decimal (0.4), then multiply by 100: 0.4 x 100 = 40%.
Q: What if the number wasn't 60? How would I adapt the method?
A: The method remains the same. Replace 60 with any other number. For example, to find 2/5 of 100, you would calculate (2/5) x 100 = 40.
Conclusion: Mastering Fractions – A Lifelong Skill
Understanding how to calculate 2/5 of 60 is more than just solving a simple arithmetic problem. It's about grasping the fundamental principles of fractions, their versatility, and their widespread applications across various disciplines. From everyday tasks like cooking and budgeting to complex calculations in engineering and finance, a solid understanding of fractions is an invaluable asset. By mastering these foundational concepts, you equip yourself with a crucial skill set applicable throughout your life, both personally and professionally. This extends beyond simply knowing how to find 2/5 of 60; it's about developing a deeper mathematical intuition and the ability to confidently tackle more complex fractional calculations in the future. The more you practice, the more comfortable and proficient you will become, and the broader the range of problems you’ll be able to solve.
Latest Posts
Latest Posts
-
L To Dl
Sep 11, 2025
-
Pmh Medical Abbrev
Sep 11, 2025
-
Qua Scrabble Word
Sep 11, 2025
-
4 2 X
Sep 11, 2025
-
92 7kg In Stone
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 2/5 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.