2/5 Of 45
stanleys
Sep 15, 2025 · 6 min read
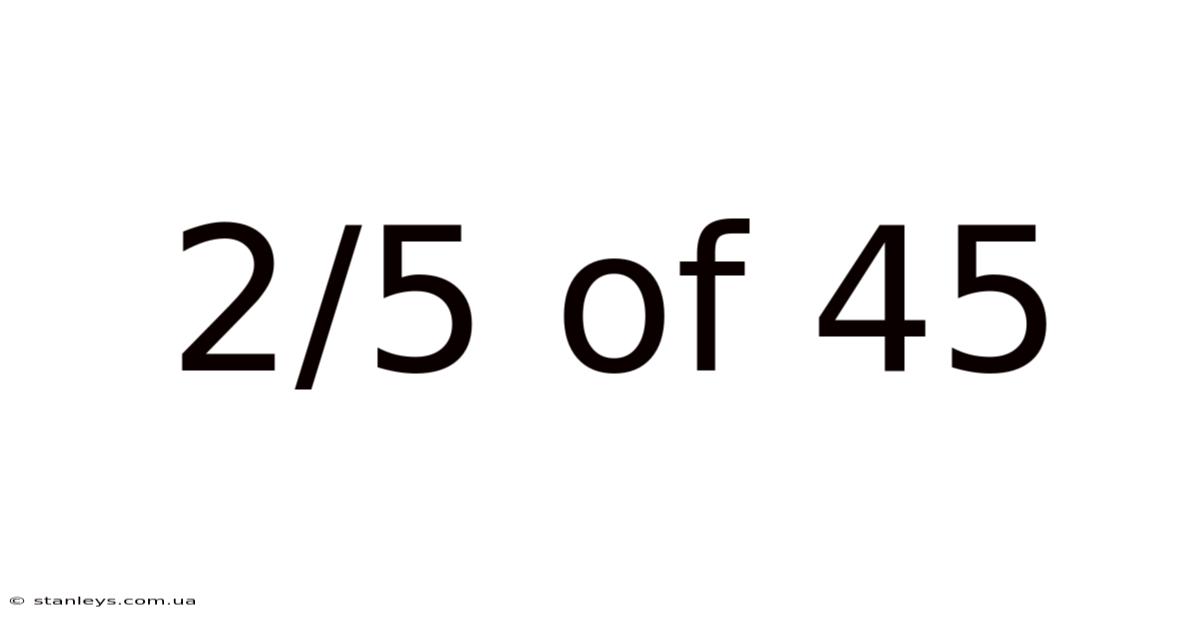
Table of Contents
Unveiling the Mystery: A Deep Dive into 2/5 of 45
Finding 2/5 of 45 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly straightforward calculation opens a door to a fascinating world of fractions, ratios, proportions, and their real-world applications. This article will not only solve the problem but also explore the underlying concepts, offering a comprehensive understanding that extends far beyond a simple numerical answer. We'll delve into different methods of solving the problem, explore its applications in various fields, and address frequently asked questions. By the end, you'll possess a confident grasp of fractions and their practical significance.
Understanding Fractions: The Building Blocks
Before tackling 2/5 of 45, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
Method 1: Direct Calculation
The most straightforward way to find 2/5 of 45 is to directly perform the calculation. We can express "of" as multiplication. Therefore, the problem becomes:
(2/5) * 45
To multiply a fraction by a whole number, we can multiply the numerator by the whole number and keep the denominator the same:
(2 * 45) / 5 = 90 / 5
Finally, we simplify the fraction by dividing the numerator by the denominator:
90 / 5 = 18
Therefore, 2/5 of 45 is 18.
Method 2: Finding the Unit Fraction
Another approach involves finding the unit fraction first. A unit fraction is a fraction with a numerator of 1. In this case, the unit fraction is 1/5. We can find 1/5 of 45 by dividing 45 by 5:
45 / 5 = 9
This means 1/5 of 45 is 9. Since we need 2/5, we simply multiply the unit fraction result by 2:
9 * 2 = 18
Again, we arrive at the answer: 2/5 of 45 is 18.
Method 3: Decimal Conversion
We can also solve this problem using decimal conversions. First, convert the fraction 2/5 into a decimal:
2 / 5 = 0.4
Then, multiply the decimal by 45:
0.4 * 45 = 18
This method highlights the interchangeable nature of fractions and decimals, reinforcing the understanding that both represent parts of a whole.
Real-World Applications: Beyond the Classroom
The concept of finding a fraction of a number isn't confined to mathematical exercises. It has widespread applications in various real-world scenarios:
-
Shopping Discounts: Imagine a store offering a 20% discount on an item priced at $45. 20% can be expressed as the fraction 1/5. Therefore, the discount amount is (1/5) * $45 = $9. The final price after the discount would be $45 - $9 = $36. Understanding fractions helps you quickly calculate discounts and make informed purchasing decisions.
-
Recipe Scaling: If a recipe calls for 2/5 of a cup of flour for 4 servings, and you want to double the recipe to make 8 servings, you would need to calculate (2/5) * 2 cups = 4/5 of a cup of flour. This demonstrates how fraction calculations are essential in cooking and baking.
-
Data Analysis: In data analysis, fractions and percentages are commonly used to represent proportions within datasets. For example, if a survey of 45 people reveals that 18 prefer a particular brand, we can express this as 18/45, which simplifies to 2/5 or 40%. This helps in understanding trends and drawing conclusions from collected data.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Fractions are often used to represent precise dimensions and quantities of materials. For example, a blueprint might specify the use of 2/5 of a cubic meter of concrete for a particular section of a building.
-
Financial Calculations: Fractions and percentages are fundamental in finance. Calculating interest rates, loan repayments, and investment returns frequently involve working with fractions. Understanding fractional calculations improves your understanding of financial statements and reports.
Exploring Ratios and Proportions
The problem of finding 2/5 of 45 is intrinsically linked to the concepts of ratios and proportions. A ratio is a comparison between two quantities, often expressed as a fraction. In this case, the ratio is 2:5, representing the relationship between the part (2) and the whole (5). A proportion is a statement of equality between two ratios. We can express the problem as a proportion:
2/5 = x/45
To solve for x (which represents 2/5 of 45), we can cross-multiply:
5x = 2 * 45
5x = 90
x = 90 / 5
x = 18
This method further reinforces the interconnectedness of fractions, ratios, and proportions, emphasizing their versatility in problem-solving.
Addressing Common Misconceptions
Several common misconceptions can arise when dealing with fractions:
-
Incorrect Order of Operations: Remember that multiplication and division have equal precedence in the order of operations (PEMDAS/BODMAS). You should perform these operations from left to right.
-
Confusing Numerator and Denominator: Always pay close attention to which number is the numerator and which is the denominator. Switching them will lead to an incorrect result.
-
Improper Simplification: Ensure you simplify fractions to their lowest terms to obtain the most concise and accurate answer.
-
Ignoring the "Of" Operator: Remember that "of" in mathematical contexts often implies multiplication.
Frequently Asked Questions (FAQ)
Q1: Can I solve this problem using a calculator?
A1: Yes, absolutely! Most calculators can handle fraction calculations directly or by converting the fraction to a decimal.
Q2: What if the numbers were different? How would I approach a similar problem?
A2: The same methods apply regardless of the numbers. The key is to understand the underlying principles of fractions and the various methods for solving them (direct calculation, unit fraction, decimal conversion, or proportion).
Q3: Are there other ways to represent 2/5?
A3: Yes, 2/5 can also be represented as a decimal (0.4) or a percentage (40%).
Q4: What if the fraction was an improper fraction (numerator larger than denominator)?
A4: The same principles still apply. You would perform the multiplication as usual and then convert the resulting improper fraction to a mixed number if required.
Conclusion: Mastering Fractions for a Brighter Future
Finding 2/5 of 45, while seemingly simple, provides a robust foundation for understanding fractions, ratios, and proportions. These mathematical concepts are not just abstract ideas; they are essential tools for navigating various aspects of daily life, from budgeting and shopping to cooking, construction, and data analysis. By mastering these fundamental principles, you equip yourself with valuable skills applicable to numerous fields and future endeavors. The journey of learning is a continuous process; remember to practice regularly and explore different approaches to solidify your understanding. The ability to confidently handle fractions unlocks a world of possibilities and empowers you to solve complex problems with ease and precision.
Latest Posts
Latest Posts
-
800 Grams Ounces
Sep 15, 2025
-
95 3kg In Stone
Sep 15, 2025
-
30 Of 110
Sep 15, 2025
-
66 6 To Fraction
Sep 15, 2025
-
Box With X
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 2/5 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.