19 X 3
stanleys
Sep 16, 2025 · 5 min read
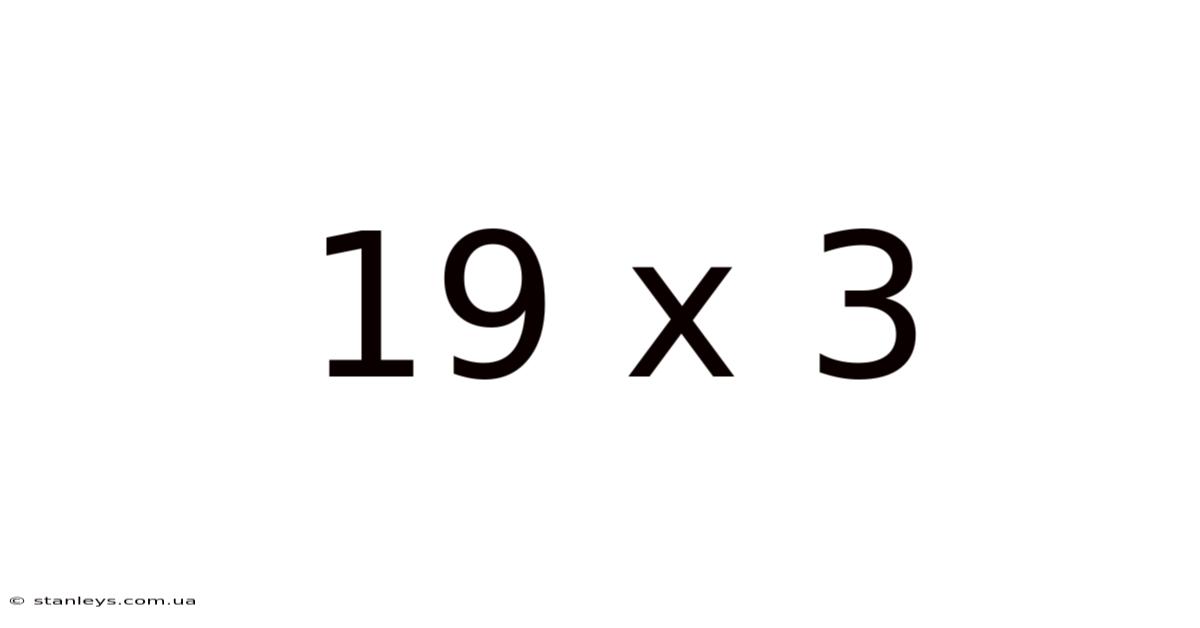
Table of Contents
Unveiling the Magic Behind 19 x 3: A Deep Dive into Multiplication
This article delves into the seemingly simple multiplication problem of 19 x 3, exploring its solution through various methods and expanding upon the underlying mathematical principles. We'll move beyond a simple answer, uncovering the rich tapestry of mathematical concepts embedded within this seemingly basic calculation. This exploration is designed to be accessible to all, from elementary school students to those looking to refresh their fundamental arithmetic skills. Understanding the 'why' behind the 'how' will strengthen your mathematical intuition and problem-solving abilities.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is simply repeated addition. When we say 19 x 3, we're essentially asking: what is the sum of three 19s? This can be represented visually as three groups of nineteen objects, whether those are apples, marbles, or abstract units.
-
Method 1: Repeated Addition: The most straightforward approach is to add 19 three times: 19 + 19 + 19 = 57. This method reinforces the basic concept of multiplication and is excellent for building a strong foundational understanding.
-
Visual Representation: Imagine three rows, each containing nineteen dots. Counting all the dots would yield the answer, visually demonstrating the concept of repeated addition. This visual approach is particularly helpful for younger learners.
Strategic Approaches to Solving 19 x 3
While repeated addition is fundamental, more efficient methods exist for larger numbers. Let's explore some strategies:
Method 2: Distributive Property
The distributive property of multiplication over addition is a powerful tool. We can break down 19 into 20 - 1, making the calculation easier:
19 x 3 = (20 - 1) x 3
Applying the distributive property:
(20 x 3) - (1 x 3) = 60 - 3 = 57
This method leverages the ease of multiplying by multiples of ten, making it a more efficient approach than direct addition.
Method 3: Partial Products
Similar to the distributive property, the partial products method breaks down the multiplication into smaller, manageable steps:
- Multiply the tens digit of 19 (which is 10) by 3: 10 x 3 = 30
- Multiply the units digit of 19 (which is 9) by 3: 9 x 3 = 27
- Add the partial products together: 30 + 27 = 57
This method clarifies the role of place value in multiplication, highlighting the contribution of each digit to the final product.
Method 4: Lattice Multiplication (A Visual Approach)
Lattice multiplication offers a unique visual approach that can be particularly helpful for those who benefit from visual aids:
- Draw a grid with two rows (for the two digits of 19) and one column (for the single digit of 3).
- Write the digits of 19 along the top and the digit 3 along the right side.
- Multiply each digit of 19 by 3 and write the result in the corresponding cell, separating the tens and units digits diagonally.
- Add the numbers along the diagonal lines, starting from the bottom right.
This method emphasizes place value and offers a systematic way to handle multiplication problems, especially beneficial for larger numbers.
The Mathematical Essence: Place Value and the Distributive Property
The success of many of these methods hinges on understanding place value and the distributive property. Place value dictates that the position of a digit within a number determines its value. In 19, the '1' represents 10 and the '9' represents 9. The distributive property allows us to break down a multiplication problem into smaller, easier calculations and then combine the results. Mastering these two concepts is crucial for proficiency in arithmetic.
Beyond the Calculation: Exploring Applications of 19 x 3
While 19 x 3 might seem like a simple isolated problem, it represents a fundamental concept applicable across numerous real-world scenarios:
-
Everyday Calculations: Calculating the total cost of 3 items priced at $19 each, determining the number of minutes in 3 hours and 19 minutes, or calculating the total distance traveled over 3 segments of a journey, each 19 kilometers long.
-
Geometry: Finding the area of a rectangle with sides measuring 19 units and 3 units.
-
Data Analysis: In data analysis, this type of calculation could represent the total number of occurrences within 3 groups of 19 data points each.
-
Scaling and Proportion: Understanding this basic multiplication empowers you to scale recipes (e.g., tripling a recipe that calls for 19 grams of an ingredient) or solve simple proportion problems.
Frequently Asked Questions (FAQ)
Q: Is there a faster way to solve 19 x 3 than repeated addition?
A: Yes, the distributive property and partial products methods offer more efficient solutions, particularly as numbers increase in size.
Q: Why is understanding place value important in this calculation?
A: Place value is crucial because it dictates the value of each digit within the number. Incorrectly handling place value leads to inaccurate results.
Q: Can I use a calculator to solve 19 x 3?
A: Yes, calculators provide a quick solution, but understanding the underlying mathematical principles is essential for developing strong mathematical skills.
Q: How can I improve my multiplication skills?
A: Practice regularly using different methods, focus on understanding place value and the distributive property, and explore various visual aids like the lattice method.
Conclusion: The Power of Understanding
The seemingly simple problem of 19 x 3 opens a window into a broader world of mathematical concepts. Understanding the multiple methods for solving this problem, and the underlying principles of place value and the distributive property, builds a strong foundation for more advanced mathematical operations. By exploring these approaches, you not only arrive at the correct answer (57) but also deepen your mathematical intuition and problem-solving skills. Remember, the goal is not just to find the answer but to understand why that answer is correct. This foundational understanding will serve you well in all your future mathematical endeavors. Keep practicing, keep exploring, and keep challenging yourself to understand the "why" behind the "how." The more you delve into the intricacies of mathematics, the more rewarding and fascinating it becomes.
Latest Posts
Related Post
Thank you for visiting our website which covers about 19 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.