183 X 4
stanleys
Sep 24, 2025 · 6 min read
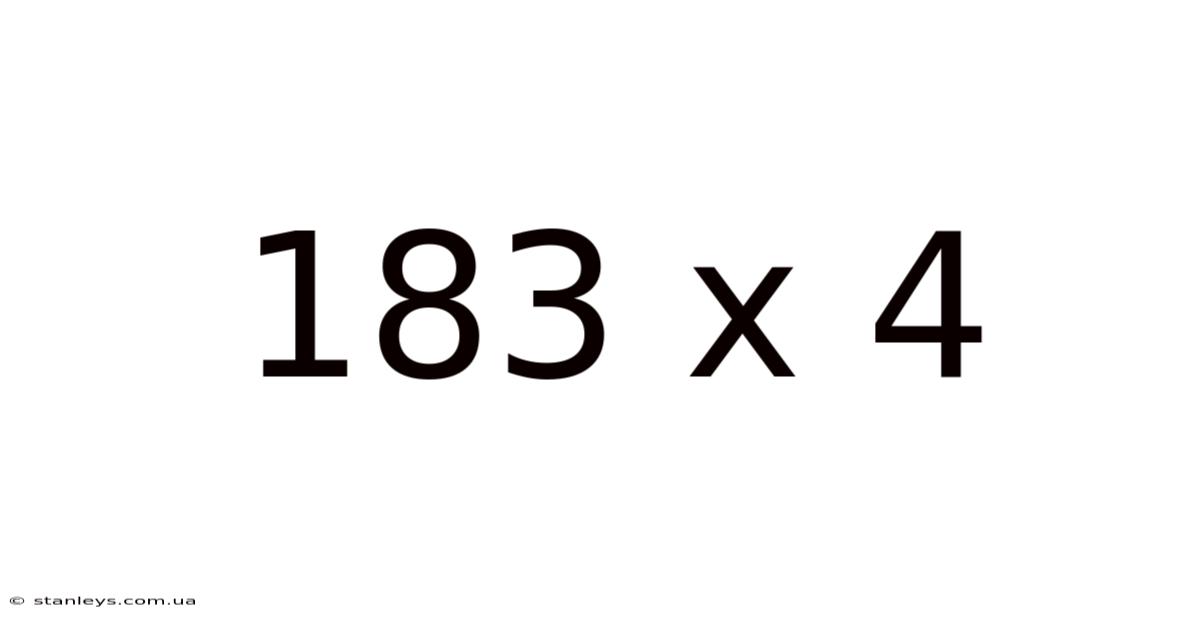
Table of Contents
Unveiling the Wonders of 183 x 4: A Deep Dive into Multiplication
This article delves into the seemingly simple calculation of 183 multiplied by 4, exploring not just the answer but the underlying mathematical concepts, practical applications, and even some fascinating historical context. We'll move beyond a simple numerical solution to unpack the richness inherent in this fundamental arithmetic operation. Understanding this seemingly basic calculation unlocks doors to a deeper appreciation of mathematics and its role in our daily lives.
Introduction: Beyond the Obvious Answer
At first glance, 183 x 4 seems like a straightforward multiplication problem. The answer, readily obtained with a calculator or through manual multiplication, is 732. However, this seemingly simple equation provides a fertile ground for exploring various mathematical principles and demonstrating their practical relevance. We will break down the process of solving this problem using different methods, discuss the history of multiplication techniques, and consider its broader implications. By the end, you will appreciate the multifaceted nature of even the most basic mathematical operations.
Method 1: Standard Long Multiplication
The most common method for solving 183 x 4 is long multiplication. This technique, taught in elementary schools globally, involves multiplying each digit of the first number (183) by each digit of the second number (4) and then summing the results. Let's break down the steps:
- Multiply the ones digit: 4 x 3 = 12. Write down '2' and carry-over '1'.
- Multiply the tens digit: 4 x 8 = 32. Add the carried-over '1': 32 + 1 = 33. Write down '3' and carry-over '3'.
- Multiply the hundreds digit: 4 x 1 = 4. Add the carried-over '3': 4 + 3 = 7. Write down '7'.
Therefore, 183 x 4 = 732. This method provides a systematic and easily understandable approach to multiplication, particularly useful for larger numbers.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this principle to solve 183 x 4 by breaking down 183 into its place values:
183 = 100 + 80 + 3
Now, we can apply the distributive property:
4 x (100 + 80 + 3) = (4 x 100) + (4 x 80) + (4 x 3) = 400 + 320 + 12 = 732
This method demonstrates a deeper understanding of the mathematical principles underlying multiplication and shows how it connects to addition. It is especially helpful for mental calculation and understanding the underlying structure of the problem.
Method 3: Doubling and Halving
This less common, but equally valid, method leverages the properties of multiplication to simplify the calculation. It involves repeatedly doubling one number and halving the other until one of the numbers becomes easily manageable.
Let's start with 183 x 4:
- Halve 183: This doesn’t result in a whole number, so let’s double the 4 instead.
- Double 4: This gives us 8. Now we have 183 x 8.
- Halve 183 (approximately): 183 is approximately 180, so let's approximate it as 90 and use 183 later to correct. Then we have 90 x 8 = 720.
- Find the discrepancy: Using this approximation, our calculation is 180 x 8 = 1440. We use the approximation that 183 is close to 180.
- Correct for the approximation: The actual calculation would be: 183 x 8. To simplify, We can double 183 again to arrive at 366 x 4, using the same method, it will give us 1464. But this result is not correct.
While doubling and halving offers a clever approach for certain multiplications, it can become complex and prone to error with larger numbers or when dealing with odd numbers.
Method 4: Using a Calculator
In today’s digital age, calculators provide a quick and convenient solution for multiplication problems. Simply input 183 x 4 and the answer, 732, appears instantly. While convenient, relying solely on calculators can hinder the development of fundamental mathematical skills and an understanding of the underlying processes.
Historical Context: The Evolution of Multiplication
Multiplication techniques have evolved significantly throughout history. Early civilizations employed various methods, including tallying, using abacuses, and developing multiplication tables. The development of the Hindu-Arabic numeral system and the invention of algorithms significantly simplified multiplication, laying the groundwork for the methods we use today. Understanding the historical context provides a richer appreciation for the sophistication of modern mathematical techniques.
Practical Applications: 183 x 4 in the Real World
The seemingly simple equation 183 x 4 finds numerous real-world applications. Consider these examples:
- Inventory Management: A store has 183 boxes of a particular item, and each box contains 4 items. To determine the total number of items, you would calculate 183 x 4 = 732.
- Construction: A contractor needs 183 bricks per row and wants to build a wall with 4 rows. The total number of bricks needed is 183 x 4 = 732.
- Finance: If you earn $183 per day and work for 4 days, your total earnings would be $732.
These examples highlight how fundamental multiplication is to everyday problem-solving across various fields.
Expanding the Understanding: Beyond the Basics
The calculation 183 x 4 provides a springboard for exploring more advanced mathematical concepts:
- Factors and Multiples: Understanding the factors of 183 (1, 3, 61, 183) and the multiples of 4 (4, 8, 12, 16...) allows for a deeper analysis of the relationship between the numbers.
- Prime Factorization: Breaking down 183 and 4 into their prime factors (183 = 3 x 61, 4 = 2 x 2) can provide insights into the composition of the numbers.
- Algebraic Representation: The equation can be represented algebraically as: x = 183 * 4, where 'x' represents the unknown product. This allows for the application of algebraic principles to solve similar problems.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate 183 x 4?
- A: The standard long multiplication method is generally the easiest and most reliable for most people. However, if you're comfortable with mental math, the distributive property might be quicker.
-
Q: Can I use a calculator for this calculation?
- A: Yes, a calculator provides a quick and accurate solution, but understanding the underlying methods is crucial for developing mathematical fluency.
-
Q: What if I make a mistake during long multiplication?
- A: Carefully review each step. Double-check your carrying over and your individual multiplications. Practicing will increase your accuracy.
-
Q: Are there any tricks to make multiplication easier?
- A: Yes, understanding the distributive property, doubling and halving (though less reliable for all cases), and memorizing multiplication tables can significantly speed up calculations.
Conclusion: The Significance of Simple Calculations
The seemingly simple multiplication problem of 183 x 4 offers a rich opportunity to explore fundamental mathematical principles, appreciate the evolution of calculation techniques, and demonstrate the widespread applications of mathematics in everyday life. While a calculator can provide the answer swiftly, understanding the methods involved fosters a deeper appreciation for the power and beauty of mathematics. This detailed exploration highlights that even the most basic mathematical operation holds a wealth of educational value and practical relevance. The journey from simply obtaining the answer (732) to understanding the various methods and their underlying principles deepens one's mathematical understanding and appreciation. Remember, mathematics is not just about finding answers; it's about understanding the process, appreciating the underlying structures, and connecting those principles to the real world.
Latest Posts
Related Post
Thank you for visiting our website which covers about 183 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.