17.5 X 2
stanleys
Sep 13, 2025 · 6 min read
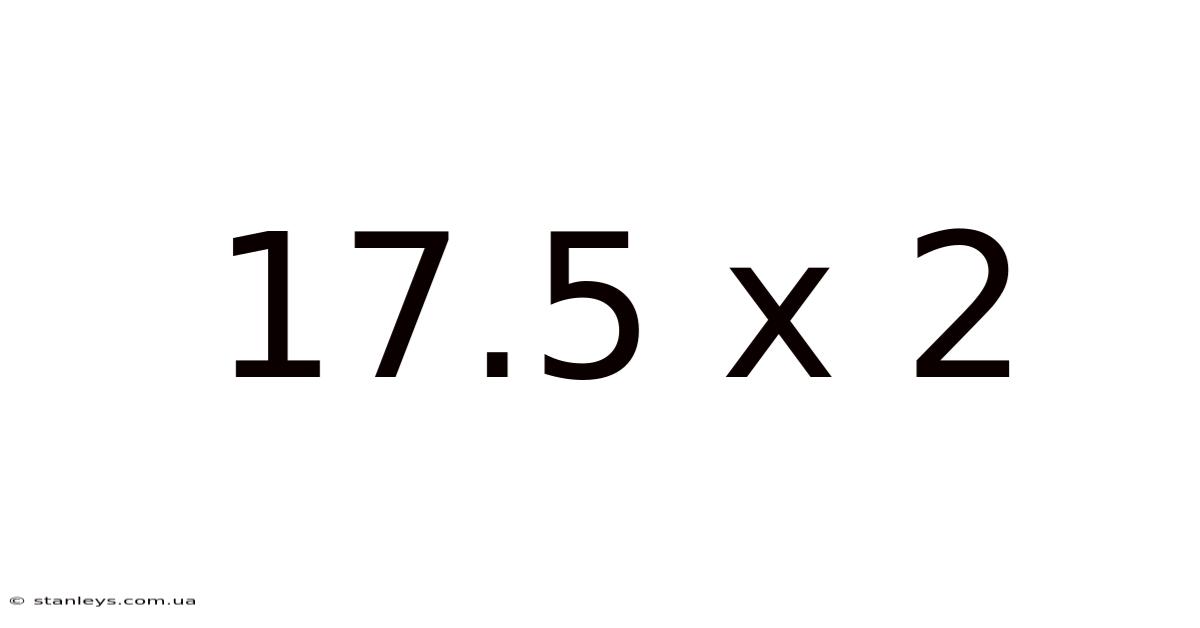
Table of Contents
Decoding 17.5 x 2: Exploring Multiplication, Fractions, and Practical Applications
This article delves into the seemingly simple calculation of 17.5 x 2, exploring the underlying mathematical principles, different methods for solving it, and its relevance in various real-world scenarios. We'll move beyond the basic answer to uncover the broader concepts involved, making this a comprehensive guide for anyone looking to strengthen their understanding of arithmetic and its practical applications. This exploration will be particularly beneficial for students grappling with fractions and decimals, and for anyone wanting a refresher on fundamental mathematical operations.
Understanding the Fundamentals: Multiplication and Decimal Numbers
Before tackling 17.5 x 2, let's solidify our understanding of the core components: multiplication and decimal numbers.
Multiplication is a fundamental arithmetic operation representing repeated addition. For example, 2 x 3 means adding 2 three times (2 + 2 + 2 = 6). In the case of 17.5 x 2, we're essentially adding 17.5 two times.
Decimal numbers are numbers that contain a decimal point, separating the whole number part from the fractional part. The number 17.5 consists of a whole number part (17) and a fractional part (0.5, which is equivalent to ½). Understanding the place value of each digit is crucial: the digit to the left of the decimal point represents the ones, tens, hundreds, and so on, while the digit to the right represents tenths, hundredths, thousandths, and so on.
Methods for Solving 17.5 x 2
There are several ways to solve 17.5 x 2, each offering a different approach and highlighting different mathematical concepts.
1. Direct Multiplication:
This is the most straightforward method. We can perform the multiplication directly, treating the decimal point as if it wasn't there initially:
175 x 2
350
Now, we reintroduce the decimal point. Since there's one digit after the decimal point in 17.5, we place the decimal point in the result one place from the right: 35.0, or simply 35.
2. Breaking Down the Numbers:
This method involves breaking down the numbers into simpler components, making the calculation easier. We can break 17.5 into 17 + 0.5:
- 17 x 2 = 34
- 0.5 x 2 = 1
Adding the results together: 34 + 1 = 35
This method is particularly useful for mental calculations and demonstrates a deeper understanding of the distributive property of multiplication.
3. Using Fractions:
Since 0.5 is equivalent to ½, we can express 17.5 as a mixed fraction: 17 ½. Then, the multiplication becomes:
2 x (17 ½) = 2 x (35/2) = 70/2 = 35
This method helps to bridge the gap between decimal numbers and fractions, strengthening understanding of both number systems.
4. Doubling:
This is a simple mental math technique. Doubling 17.5 means adding 17.5 to itself: 17.5 + 17.5 = 35. This method is efficient for quick calculations, particularly with numbers that are easily doubled.
Practical Applications of 17.5 x 2
The calculation 17.5 x 2 appears in various real-world contexts. Here are a few examples:
- Shopping: If you buy two items priced at $17.50 each, the total cost will be 17.5 x 2 = $35.
- Cooking: If a recipe calls for 17.5 grams of an ingredient and you need to double the recipe, you'll need 17.5 x 2 = 35 grams.
- Construction: If you're working with materials measured in meters and need to double a length of 17.5 meters, the total length becomes 17.5 x 2 = 35 meters.
- Finance: Calculating the total value of two investments, each worth $17.50, results in 17.5 x 2 = $35.
- Sports: If an athlete completes two laps of a track, each measuring 17.5 meters, the total distance covered is 17.5 x 2 = 35 meters.
These are just a few basic examples; the application extends across numerous fields and daily activities.
Extending the Concept: Working with Larger Numbers and More Complex Calculations
The principles discussed in relation to 17.5 x 2 can be extended to more complex calculations. For example, consider 17.5 x 3, 17.5 x 10, or even 17.5 x 2.5. The same methods – direct multiplication, breaking down numbers, using fractions, or even leveraging mental math techniques – can be applied.
Let's consider 17.5 x 10. This is easily solved by moving the decimal point one place to the right, resulting in 175. This is because multiplying by 10 is equivalent to multiplying by 10¹, which involves shifting the decimal point one place to the right. Similarly, multiplying by 100 (10²) involves shifting the decimal point two places to the right, and so on.
For calculations involving more complex decimal numbers or larger multipliers, using a calculator may be more efficient, but understanding the underlying mathematical principles remains crucial for interpreting results and for developing strong number sense.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand different methods for solving 17.5 x 2?
A1: Understanding different methods cultivates a deeper understanding of the underlying mathematical concepts. It provides flexibility in approaching problems, allowing you to choose the most efficient method depending on the context. It also enhances problem-solving skills and improves mental arithmetic abilities.
Q2: Can I use a calculator for this calculation?
A2: Absolutely! Calculators are useful tools for efficiency, especially with more complex calculations. However, it’s important to also understand the underlying mathematical principles to avoid relying solely on the calculator and to develop strong number sense.
Q3: How does understanding 17.5 x 2 help me in more advanced mathematics?
A3: This fundamental calculation provides a strong foundation for understanding more advanced topics like algebra, where similar principles of multiplication and manipulating decimal numbers are extensively used. It’s a stepping stone towards grasping more complex mathematical concepts.
Q4: What if the number was 17.5 x 2.5? How would I solve that?
A4: You could use the same principles. You could break down 2.5 into 2 + 0.5, then multiply 17.5 by each part separately and add the results. Alternatively, you could convert both numbers into fractions (17.5 = 35/2 and 2.5 = 5/2) and then multiply the fractions: (35/2) x (5/2) = 175/4 = 43.75. Or, you could use direct multiplication with decimals.
Conclusion: Beyond the Answer
The seemingly simple calculation of 17.5 x 2 offers a rich opportunity to explore fundamental mathematical principles, different problem-solving strategies, and practical applications in everyday life. By understanding the various methods for solving this calculation and by relating it to real-world situations, we build a stronger foundation in mathematics, improve our problem-solving skills, and appreciate the power of numerical literacy in navigating the world around us. It’s not just about getting the answer (35); it's about understanding why the answer is 35 and how this understanding can be applied to a wide range of situations. This deeper understanding is crucial for success in further mathematical studies and in countless real-world applications.
Latest Posts
Latest Posts
-
155 In Kg
Sep 13, 2025
-
Mashed Potato Scoop
Sep 13, 2025
-
1500ml In Pints
Sep 13, 2025
-
Red Color Yellow
Sep 13, 2025
-
140 X 3
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 17.5 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.