15 Of 900
stanleys
Sep 06, 2025 · 6 min read
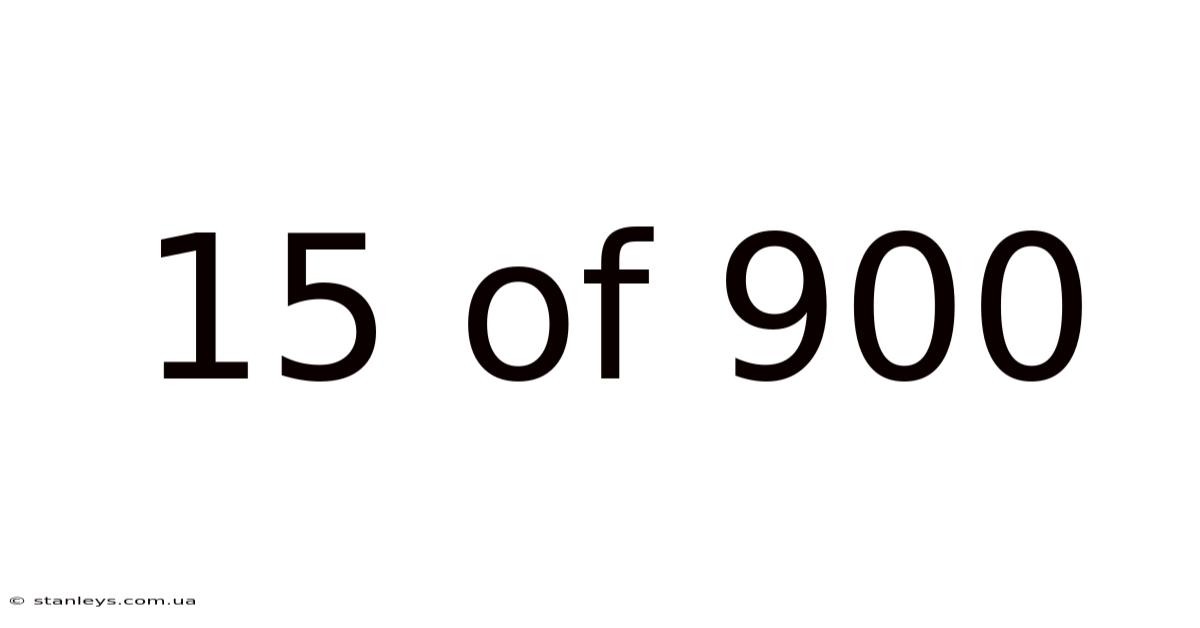
Table of Contents
Unveiling the Mystery: Understanding 15 out of 900 – A Deep Dive into Percentages, Ratios, and Probabilities
Understanding fractions, percentages, and probabilities is crucial in many aspects of life, from everyday tasks to complex scientific calculations. This article delves into the seemingly simple question: "What does 15 out of 900 represent?" We'll explore this seemingly simple problem, unpacking the underlying concepts and showing how this single example can illuminate a vast landscape of mathematical understanding. This includes calculating percentages, simplifying ratios, understanding relative frequencies, and even touching upon the implications for probability calculations. This detailed analysis will be beneficial for students, professionals, and anyone seeking a clearer grasp of these fundamental mathematical principles.
Converting the Ratio: From Fraction to Percentage
The core of understanding "15 out of 900" lies in recognizing it as a ratio. It can be expressed as a fraction: 15/900. This fraction represents the proportion of 15 relative to the total of 900. To convert this ratio into a more readily understandable format, we calculate the percentage.
The process involves dividing the numerator (15) by the denominator (900) and then multiplying the result by 100:
(15/900) * 100 = 1.666...%
This means that 15 out of 900 represents approximately 1.67%. The recurring decimal indicates that this percentage is an approximation; the exact value is a non-terminating decimal. Understanding this approximation is key to interpreting the results in real-world contexts.
Simplifying the Fraction: Finding the Lowest Terms
Before moving to more advanced applications, it's essential to simplify the original fraction 15/900. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In this case, the GCD of 15 and 900 is 15.
Dividing both the numerator and denominator by 15, we get:
15/15 = 1 900/15 = 60
Therefore, the simplified fraction is 1/60. This simplified form is crucial for understanding the underlying ratio more clearly. It shows that 15 out of 900 is equivalent to one part out of every sixty parts.
Exploring the Concept of Relative Frequency
In statistics, the phrase "15 out of 900" would represent a relative frequency. Imagine a survey where 900 people were asked a question, and 15 responded in a particular way. The relative frequency of that response is 15/900, or 1/60, or approximately 1.67%. Relative frequency provides a way to express the proportion of an event's occurrence within a larger dataset. This is invaluable in analyzing data and drawing conclusions from it. For instance, if this represented the number of defective items in a batch of 900, the relative frequency would indicate the defect rate.
Applications in Probability
The ratio 15/900 can also be interpreted within the framework of probability. If we imagine a scenario where we randomly select one item from a set of 900 items, and 15 of those items possess a particular characteristic, the probability of selecting an item with that characteristic is 15/900, or 1/60, or approximately 1.67%.
Probability is expressed as a value between 0 and 1, where 0 indicates an impossible event, and 1 indicates a certain event. Our probability of 1/60 (or 0.0167) signifies a relatively low chance of selecting an item with the specified characteristic.
Expanding the Context: Real-World Examples
Let's illustrate how "15 out of 900" can be applied in different scenarios:
- Quality Control: In a manufacturing process, if 15 out of 900 items are defective, the defect rate is 1.67%. This information is crucial for improving the manufacturing process.
- Surveys and Polls: If 15 out of 900 respondents answered "yes" to a specific question, the relative frequency of "yes" responses is 1.67%. This helps in understanding public opinion.
- Scientific Experiments: If 15 out of 900 experimental trials yielded a positive result, the success rate is 1.67%. This helps in evaluating the effectiveness of the experiment's design or methodology.
- Sports Statistics: If a basketball player makes 15 out of 900 free throws, their free-throw percentage is 1.67%. This is a common way to represent a player’s shooting accuracy.
Understanding the Significance of Sample Size
The context of the number 900 is crucial. It represents the sample size or the total number of observations. A larger sample size generally leads to more reliable conclusions. If the same ratio (15 out of 900) were found in a smaller sample size (e.g., 15 out of 100), the result would be more subject to chance variation and less statistically significant. This highlights the importance of considering the sample size when interpreting percentages and probabilities.
The Importance of Precision and Rounding
While we rounded the percentage to 1.67%, it's important to remember the exact value is 1.666...%. The level of precision needed depends on the context. In some situations, rounding to the nearest whole number (2%) might be sufficient, while in others, more decimal places are necessary for accuracy. This understanding helps to avoid misinterpretations due to rounding errors.
Further Mathematical Explorations: Proportions and Ratios
The ratio 15:900 (or 1:60) allows for further mathematical explorations of proportions. We could use this ratio to calculate the number of items with the same characteristic in a larger or smaller sample size. For example:
- If we had a sample of 1800 items, we would expect approximately 30 (1800 * 1/60) to have the same characteristic.
- If we had a sample of 300 items, we would expect approximately 5 (300 * 1/60) to have the same characteristic.
This ability to extrapolate from the known ratio to different sample sizes demonstrates the power of understanding ratios and proportions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to find the percentage?
A: Absolutely! Dividing 15 by 900 and then multiplying by 100 is easily done using any calculator.
Q: Why is it important to simplify the fraction?
A: Simplifying the fraction makes the ratio easier to understand and allows for easier calculations. 1/60 is much more intuitive than 15/900.
Q: What if the numbers were different? How would I approach a similar problem?
A: The same principles apply. For any "X out of Y" situation, calculate X/Y and multiply by 100 to get the percentage. Always simplify the fraction to its lowest terms.
Q: Is there a software or online tool that can help with these calculations?
A: Many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) can perform these calculations quickly and accurately.
Conclusion: The Power of Understanding Ratios and Percentages
Understanding the meaning of "15 out of 900" extends far beyond a simple calculation. It involves grasping fundamental concepts of ratios, fractions, percentages, relative frequencies, and probabilities. The ability to convert ratios to percentages, simplify fractions, and apply these concepts in different contexts is a valuable skill with applications across various fields, from statistics and science to business and everyday life. This detailed exploration has aimed to not only answer the initial question but also equip readers with a deeper understanding of the underlying mathematical principles. By mastering these concepts, one gains a powerful tool for analyzing data, making informed decisions, and interpreting information more effectively.
Latest Posts
Latest Posts
-
Fraction Of 0 04
Sep 09, 2025
-
Megagrams To Micrograms
Sep 09, 2025
-
61 3kg In Stone
Sep 09, 2025
-
6 2kg In Stone
Sep 09, 2025
-
Coat In French
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 900 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.