15 Of 85
stanleys
Sep 12, 2025 · 6 min read
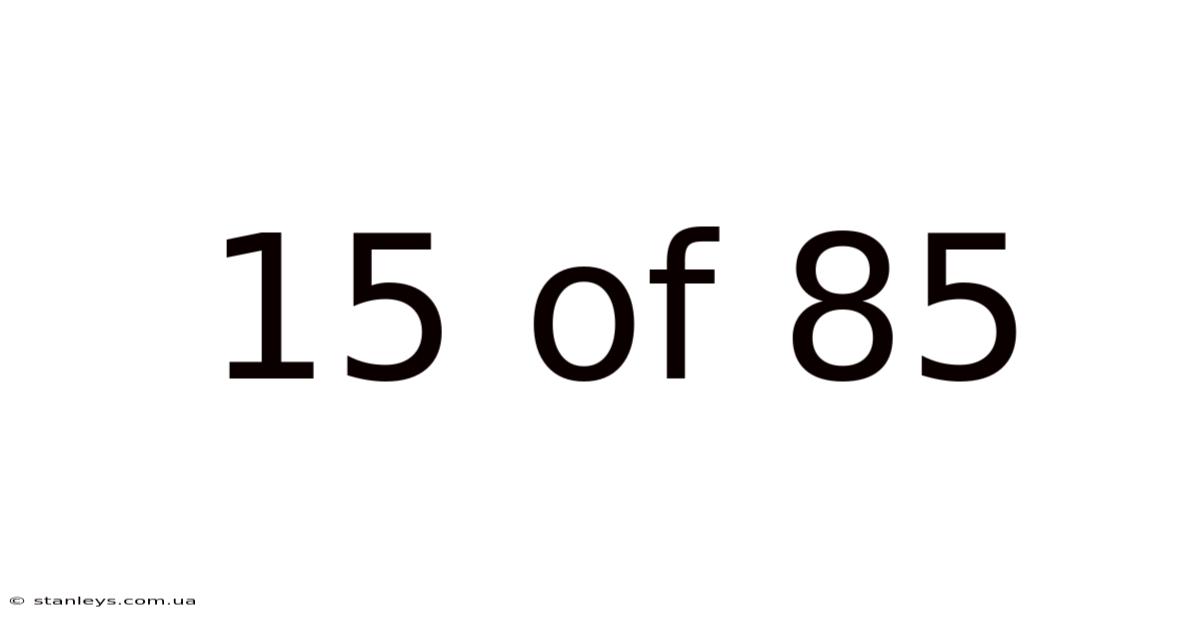
Table of Contents
Decoding the Enigma: Understanding 15 out of 85 – A Deep Dive into Proportions, Percentages, and Real-World Applications
Understanding fractions, percentages, and proportions is fundamental to navigating the complexities of everyday life. From calculating discounts at the mall to understanding complex data in scientific research, the ability to interpret and manipulate these numerical concepts is invaluable. This article will delve into the meaning and significance of "15 out of 85," exploring its representation as a fraction, percentage, and its applications across various fields. We'll also cover related concepts and answer frequently asked questions to provide a comprehensive understanding. Keyword: 15 out of 85, fraction, percentage, proportion, ratio.
Introduction: What Does "15 out of 85" Mean?
The phrase "15 out of 85" represents a ratio or proportion. It signifies that 15 items or units are selected or present from a total of 85 items or units. This simple phrase holds significant mathematical weight and can be expressed in several different, yet equally valid, ways. Understanding how to express this ratio and its implications is crucial for making informed decisions and solving various problems.
Expressing "15 out of 85" as a Fraction
The most straightforward way to represent "15 out of 85" is as a fraction: 15/85. This fraction indicates that 15 is the numerator (the part) and 85 is the denominator (the whole). However, fractions are often simplified to their lowest terms for easier understanding and comparison. To simplify 15/85, we find the greatest common divisor (GCD) of 15 and 85, which is 5. Dividing both the numerator and denominator by 5, we get the simplified fraction: 3/17. This means that for every 17 items, 3 are selected.
Converting the Fraction to a Percentage
While the fraction 3/17 provides a clear representation of the ratio, percentages offer a more readily understood and commonly used method of expressing proportions. To convert the fraction 3/17 into a percentage, we perform the following calculation:
(3/17) * 100% ≈ 17.65%
Therefore, "15 out of 85" is approximately equivalent to 17.65%. This percentage signifies that approximately 17.65 out of every 100 items would be selected if the same proportion were maintained.
Understanding Proportions and Ratios: Beyond the Numbers
The concept of "15 out of 85" extends beyond a simple numerical representation. It embodies the broader mathematical concept of proportion. A proportion is a statement of equality between two ratios. For example, the proportion 15/85 = 3/17 shows that these two ratios are equivalent. Understanding proportions is crucial for solving problems involving scaling, similarity, and direct/inverse relationships.
Consider this scenario: A school has 85 students, and 15 of them are enrolled in a music program. This represents the ratio 15/85, or 3/17. If the school expands to 170 students and maintains the same proportion of students in the music program, we can use proportions to determine how many students would be enrolled:
(3/17) = x/170
Solving for x (the number of students in the music program), we find x = 30. This demonstrates how understanding proportions enables us to predict outcomes based on existing ratios.
Real-World Applications of Proportions and Percentages
The ability to understand and apply the principles of proportions and percentages is vital in countless real-world scenarios, including:
- Business and Finance: Calculating profit margins, discounts, interest rates, and investment returns all rely heavily on understanding percentages and ratios.
- Science and Engineering: Scientific experiments often involve analyzing data and interpreting results based on proportions and percentages. Engineering designs rely on precise calculations involving ratios and proportions to ensure structural integrity and functionality.
- Statistics and Data Analysis: Analyzing statistical data often involves calculating percentages, proportions, and ratios to draw meaningful conclusions and identify trends. Understanding these concepts is essential for interpreting surveys, polls, and other forms of data.
- Everyday Life: Calculating tips at restaurants, understanding sales tax, and comparing prices all utilize the concepts of percentages and proportions. Even tasks as simple as cooking from a recipe often involve adjusting ingredient quantities based on proportions.
Beyond Simple Ratios: Exploring More Complex Scenarios
While "15 out of 85" provides a relatively straightforward example, the principles discussed extend to more intricate situations. Consider scenarios involving multiple ratios, complex fractions, or situations requiring multiple steps to reach a solution. For instance, imagine a situation where you need to compare the ratio of students enrolled in music to the ratio of students enrolled in sports. This requires a deeper understanding of comparative proportions. Mastering this involves a good grasp of fundamental concepts like cross-multiplication and solving for unknown variables in equations.
A Deeper Dive into Percentage Calculations
Calculating percentages can sometimes be more challenging than it initially seems. For instance, consider calculating the percentage increase or decrease between two values. If the number of students enrolled in music increased from 15 to 20, the percentage increase would be calculated as follows:
[(20 - 15) / 15] * 100% = 33.33%
Similarly, calculating percentage decrease follows a similar pattern. These calculations are vital in various contexts, from tracking economic growth to monitoring changes in environmental indicators.
Addressing Potential Errors and Misconceptions
One common error is incorrectly interpreting percentages. For example, a 20% increase followed by a 20% decrease does not result in the original value. This highlights the importance of understanding the underlying mathematical principles rather than relying solely on intuitive estimations. Another common misconception involves confusing ratios with percentages. While closely related, they represent different ways of expressing proportions and require careful interpretation in different contexts.
Frequently Asked Questions (FAQ)
-
Q: How do I convert a percentage to a fraction? A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 25% becomes 25/100, which simplifies to 1/4.
-
Q: How do I calculate the percentage of a number? A: To calculate the percentage of a number, multiply the number by the percentage (expressed as a decimal). For example, 20% of 50 is 0.20 * 50 = 10.
-
Q: What is the difference between a ratio and a proportion? A: A ratio is a comparison of two quantities, while a proportion is a statement that two ratios are equal.
-
Q: Can a ratio be expressed as a decimal? A: Yes, a ratio can be expressed as a decimal by dividing the numerator by the denominator. For example, the ratio 3/17 is approximately equal to 0.1765.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand and compare. It also helps in calculations, especially when dealing with more complex problems involving fractions and proportions.
Conclusion: Mastering the Power of Proportions
Understanding "15 out of 85," and more broadly, the concepts of fractions, percentages, and proportions, is essential for success in various academic, professional, and personal endeavors. This seemingly simple ratio holds significant mathematical power, allowing us to analyze data, predict outcomes, and make informed decisions in a wide range of contexts. By mastering these fundamental mathematical concepts, we empower ourselves to navigate the complexities of our world with greater confidence and understanding. The ability to translate between fractions, percentages, and ratios provides a versatile toolset for solving problems and interpreting information in a clear and concise manner. Continue to practice these skills, and you will find that their application extends far beyond simple arithmetic, opening doors to a deeper appreciation of the numerical world around us.
Latest Posts
Latest Posts
-
Double Bend Sign
Sep 12, 2025
-
Rosa Parks Quotes
Sep 12, 2025
-
Sliding Theory Filament
Sep 12, 2025
-
Traffic Bunching Meaning
Sep 12, 2025
-
Sewing A Garment
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.