125 X 12
stanleys
Sep 21, 2025 · 6 min read
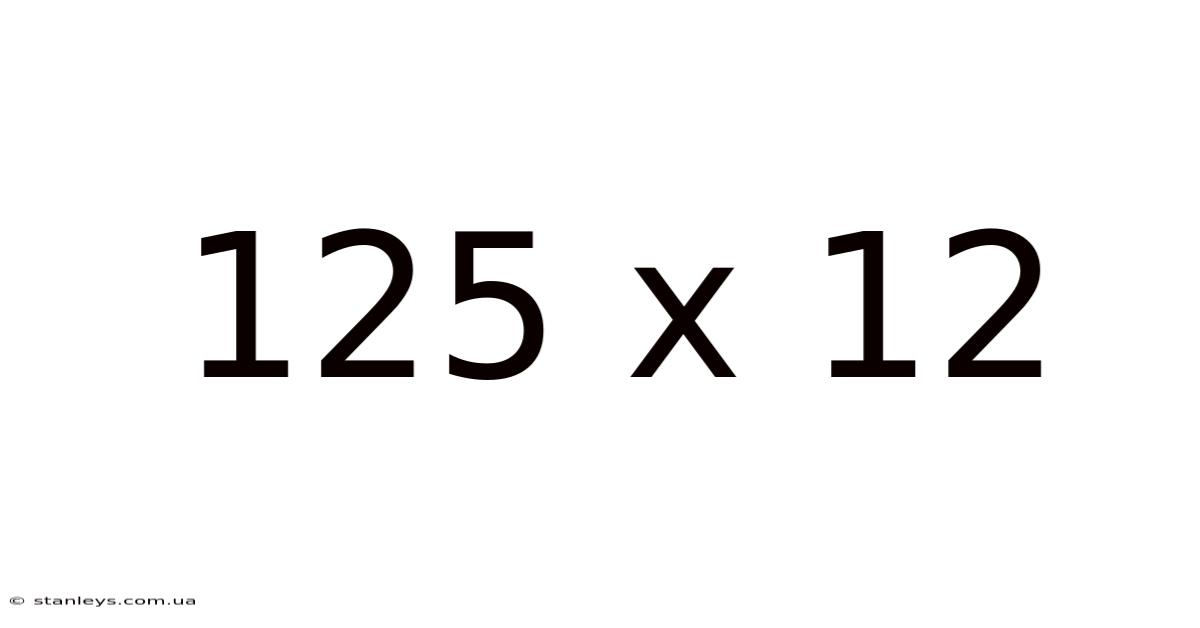
Table of Contents
Decoding 125 x 12: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 125 x 12, delving far beyond the immediate answer. We'll unravel the mechanics of multiplication, explore various methods of calculation, examine the problem's relevance in different contexts, and touch upon the broader mathematical concepts it represents. Understanding this seemingly simple equation provides a gateway to grasping more complex mathematical ideas. Whether you're a student brushing up on your multiplication skills or an adult looking to refresh your foundational math knowledge, this comprehensive guide will provide valuable insights.
I. Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is simply repeated addition. The equation 125 x 12 means adding 125 twelve times: 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125 + 125. While this method works, it’s incredibly inefficient for larger numbers. That’s where the power of multiplication shines, providing a shortcut to achieve the same result much faster.
II. Methods for Solving 125 x 12
Several methods can solve 125 x 12. Let's explore a few:
-
Standard Algorithm (Long Multiplication): This is the most common method taught in schools. It involves multiplying each digit of one number by each digit of the other, aligning the partial products, and then adding them together.
125 x 12 ----- 250 (125 x 2) 1250 (125 x 10) ----- 1500 -
Distributive Property: This method leverages the distributive property of multiplication over addition. We break down 12 into smaller, easier-to-handle numbers (like 10 and 2).
125 x 12 = 125 x (10 + 2) = (125 x 10) + (125 x 2) = 1250 + 250 = 1500
-
Mental Math Techniques: With practice, you can develop mental math skills to solve this quickly. For example, you can recognize that 125 is one-eighth of 1000. Therefore, 125 x 12 can be calculated as (1000/8) x 12. Rearranging, this becomes 1000 x (12/8) = 1000 x (3/2) = 1500. This method requires familiarity with fractions and their equivalents.
-
Using a Calculator: While not a method promoting understanding, calculators offer a quick and reliable solution, particularly for more complex problems.
III. Real-World Applications: Where do we encounter 125 x 12?
While 125 x 12 might seem like an abstract mathematical problem, its applications are surprisingly diverse:
-
Inventory Management: Imagine a warehouse storing boxes of goods. If each box contains 125 items, and there are 12 boxes, calculating the total number of items (1500) is crucial for efficient stock management.
-
Construction and Engineering: In construction projects, calculating material quantities is essential. If a project requires 125 units of a specific material per section, and there are 12 sections, knowing the total requirement (1500 units) is critical for budgeting and procurement.
-
Finance and Budgeting: Consider a scenario where monthly expenses are $125, and you need to budget for 12 months. Calculating the annual expense ($1500) is essential for financial planning.
-
Agriculture: In farming, if a farmer harvests 125 bushels of wheat per acre and has 12 acres, knowing the total harvest (1500 bushels) is crucial for yield estimation and market analysis.
-
Education: The problem serves as a fundamental exercise for students learning multiplication, strengthening their computational skills and problem-solving abilities.
IV. Expanding the Understanding: Exploring Related Concepts
Solving 125 x 12 opens doors to exploring broader mathematical concepts:
-
Factors and Multiples: The numbers 125 and 12 have their own sets of factors. Understanding factors and multiples helps in simplifying calculations and recognizing patterns in numbers. For instance, recognizing that 12 is a multiple of 2 and 6 can be beneficial in solving related problems using the distributive property.
-
Prime Factorization: Breaking down 125 and 12 into their prime factors (125 = 5 x 5 x 5; 12 = 2 x 2 x 3) provides insights into the fundamental building blocks of these numbers. This concept is crucial in various areas of mathematics, including number theory and cryptography.
-
Order of Operations (PEMDAS/BODMAS): While 125 x 12 is straightforward, understanding the order of operations is vital when dealing with more complex equations that involve multiple operations (parentheses/brackets, exponents/orders, multiplication and division, addition and subtraction).
-
Algebraic Representation: The problem can be represented algebraically as 'x = 125 * 12', where 'x' represents the unknown quantity. This introduces the concept of variables and equations, forming the foundation of algebra.
V. Beyond the Numbers: Developing Mathematical Fluency
Mastering multiplication, even a seemingly simple problem like 125 x 12, goes beyond just getting the right answer. It’s about developing mathematical fluency – the ability to understand, apply, and connect mathematical concepts with confidence and flexibility. This fluency is crucial for success in higher-level mathematics, science, engineering, and various other fields.
VI. Addressing Common Challenges and FAQs
-
Difficulty with Multiplication Tables: Many students struggle with memorizing multiplication tables. Consistent practice, using flashcards, and engaging in interactive games can help overcome this challenge.
-
Understanding the Standard Algorithm: The standard algorithm can sometimes seem confusing, particularly for larger numbers. Breaking down the problem into smaller steps, using visual aids, and focusing on understanding the underlying principles can enhance comprehension.
-
Making Mistakes in Calculation: Errors are common, especially when working with larger numbers or under time pressure. Careful attention to detail, double-checking answers, and practicing regularly can minimize errors.
-
Q: Are there alternative methods for solving this problem aside from the ones mentioned? A: Yes, there are various other mental math tricks and techniques that can be employed depending on individual preferences and familiarity with different mathematical approaches. For instance, some might find it easier to break down 125 into 100 + 25 and then multiply each part by 12 separately.
-
Q: How does solving this problem contribute to learning more advanced mathematics? A: Mastering basic arithmetic like multiplication forms a solid foundation for learning more complex concepts in algebra, calculus, and other advanced mathematical fields. It enhances number sense, problem-solving skills, and the ability to work with abstract mathematical ideas.
-
Q: What if I still struggle with multiplication after practicing? A: Seeking help from a teacher, tutor, or using online resources specifically designed for remedial math can provide additional support and guidance. There are numerous apps and websites that provide interactive learning experiences tailored to different learning styles.
VII. Conclusion: The Significance of Foundational Math Skills
The seemingly simple problem, 125 x 12, serves as a powerful illustration of the importance of foundational math skills. Understanding the various methods for solving the problem, its real-world applications, and the related mathematical concepts lays the groundwork for success in more advanced mathematical endeavors. Consistent practice, a focus on understanding underlying principles, and seeking help when needed are key to mastering multiplication and developing mathematical fluency. This fluency is not merely about getting the right answer; it's about fostering critical thinking, problem-solving skills, and a deeper appreciation for the power and elegance of mathematics. The journey from understanding 125 x 12 to mastering more complex mathematical concepts is a continuous process of learning, exploration, and growth.
Latest Posts
Related Post
Thank you for visiting our website which covers about 125 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.