10000 / 60
stanleys
Sep 15, 2025 · 6 min read
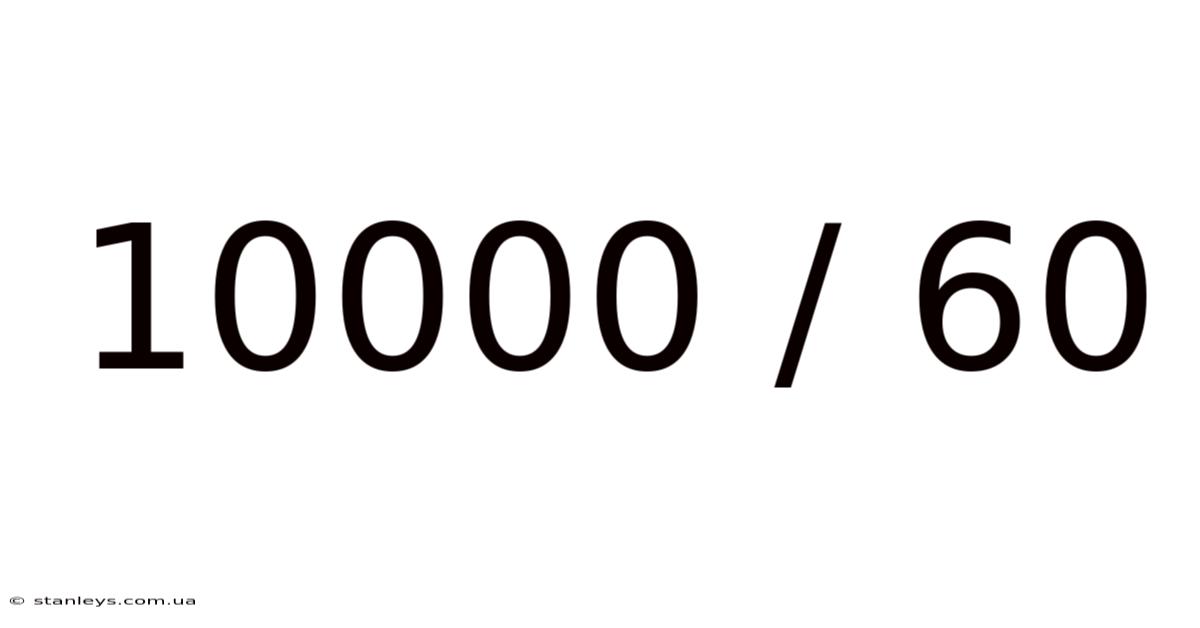
Table of Contents
Decoding 10000 / 60: A Deep Dive into Division and its Applications
This article explores the seemingly simple mathematical operation of 10000 divided by 60, delving beyond the immediate answer to uncover its underlying principles and diverse applications across various fields. We'll examine the process of long division, explore the resulting decimal and its practical interpretations, and touch upon the relevance of this calculation in real-world scenarios, from everyday life to complex scientific computations. Understanding 10000 / 60 isn't just about finding a numerical result; it's about grasping the fundamental concepts of division and its far-reaching implications.
Understanding the Problem: 10000 / 60
At its core, the problem 10000 / 60 asks: "How many times does 60 fit into 10000?" This fundamental question forms the basis of division, a crucial arithmetic operation used to separate a quantity into equal parts. The number 10000 is the dividend (the number being divided), and 60 is the divisor (the number we're dividing by). The result we're seeking is the quotient.
Performing Long Division: A Step-by-Step Guide
While calculators offer a quick solution, understanding the manual process of long division provides valuable insight into the mathematical logic involved. Here's how to solve 10000 / 60 using long division:
-
Set up the problem: Write 10000 inside the long division symbol (⟌) and 60 outside.
-
Divide the first digits: 60 doesn't go into 10, so we consider the first three digits: 100. 60 goes into 100 once (1 x 60 = 60). Write '1' above the '0' in 100.
-
Subtract and bring down: Subtract 60 from 100, leaving 40. Bring down the next digit (0) to make it 400.
-
Repeat the process: 60 goes into 400 six times (6 x 60 = 360). Write '6' above the '0' in 400.
-
Subtract and bring down: Subtract 360 from 400, leaving 40. Bring down the final digit (0) to make it 400.
-
Final division: 60 goes into 400 six times (6 x 60 = 360). Write '6' above the last '0'.
-
Subtract and determine the remainder: Subtract 360 from 400, leaving 40. This is the remainder.
Therefore, 10000 divided by 60 is 166 with a remainder of 40. We can express this as 166 R40.
Expressing the Result as a Decimal
While the remainder form is valid, it's often more useful to express the result as a decimal. To do this, we continue the long division process beyond the whole number quotient.
-
Add a decimal point and zeros: Add a decimal point after the 166 and add zeros to the dividend (10000.000...).
-
Continue dividing: Continue the long division process, bringing down zeros as needed until you reach a desired level of accuracy or the remainder becomes zero (in this case, it will be a recurring decimal).
Following this process, you find that 10000 / 60 = 166.6666... This is a recurring decimal, often written as 166.6̅.
Practical Applications of 10000 / 60
The result of 10000 / 60, whether expressed as a whole number with a remainder or a decimal, has numerous practical applications across diverse fields:
-
Time Management: If you have 10,000 seconds, dividing by 60 gives you the equivalent time in minutes (approximately 166.67 minutes). This is helpful for scheduling tasks, project management, or analyzing time-based data.
-
Unit Conversion: Many unit conversions involve division. For example, if you have 10,000 centimeters and need to convert it to meters (100 centimeters per meter), the calculation is analogous to 10000 / 100. Similarly, the division could be relevant in converting other units like feet to yards or gallons to quarts.
-
Resource Allocation: Imagine distributing 10,000 items evenly among 60 recipients. The quotient (166.67) represents the approximate number of items each recipient would receive. The remainder highlights the need for careful handling of the extra items.
-
Financial Calculations: The calculation could represent the division of a large sum of money among multiple stakeholders or the calculation of equal payments over a period.
-
Scientific Computations: In many scientific disciplines, such as physics and engineering, divisions are fundamental for calculations involving rates, ratios, and averages.
-
Statistical Analysis: Division is crucial for calculating means, medians, and other statistical measures. The result of 10000/60 could be part of a larger statistical analysis involving population distribution or sample sizes.
-
Data Analysis: In computer science and data analysis, this calculation could represent tasks such as dividing a large dataset into smaller, manageable chunks for processing or calculating an average value within a specific range.
-
Engineering and Design: Division plays a vital role in various engineering calculations, from determining the load capacity of a structure to analyzing fluid flow rates.
The Significance of Remainders
It's important to understand the significance of the remainder (40 in this case). The remainder indicates that the division isn't perfectly even. In real-world applications, the remainder may need to be addressed:
-
Rounding: Depending on the context, you might round the quotient up or down. For example, if distributing items, you might round up to ensure everyone receives at least 167 items.
-
Distribution: The remainder represents the extra items that need to be distributed separately or accounted for differently.
-
Further Calculation: In some cases, the remainder is incorporated into further calculations.
Exploring Further: Beyond 10000 / 60
The example of 10000 / 60 offers a gateway to understanding the broader implications of division. The same principles apply to any division problem, regardless of the complexity of the numbers involved. The ability to accurately and efficiently perform and interpret division is a crucial skill across various academic disciplines and professions.
Frequently Asked Questions (FAQ)
-
What if I use a calculator? A calculator provides the quick answer (166.666...). However, understanding the long division process offers deeper insight into the mathematical principles at play.
-
What are some real-world examples beyond those listed? Consider the allocation of resources in a manufacturing process, dividing a total workload among employees, or calculating the average speed of a vehicle over a certain distance. The possibilities are vast.
-
Why is it important to understand the remainder? The remainder reflects the inexact nature of the division and impacts how the result is interpreted and applied in real-world scenarios.
-
What if the divisor was a decimal number? The process remains similar, but requires a slightly different approach to managing the decimal points during long division.
-
How can I improve my division skills? Practice is key! Start with simpler division problems and gradually increase the complexity.
Conclusion
The seemingly simple calculation of 10000 / 60 provides a valuable learning opportunity extending far beyond just finding the answer. By exploring the long division process, examining the significance of the decimal and remainder, and considering its myriad applications, we gain a profound understanding of the fundamental principles of division and its vital role in numerous real-world contexts. This understanding empowers individuals to tackle more complex mathematical problems and apply these skills effectively in their chosen field. The journey from the basic problem to a deeper grasp of its implications highlights the beauty and practicality of mathematics. From time management to resource allocation, from statistical analysis to engineering design, the ability to understand and apply division is a fundamental skill with wide-ranging impact.
Latest Posts
Latest Posts
-
181 Cm Inches
Sep 15, 2025
-
Flesh Is Grass
Sep 15, 2025
-
78 6kg In Stone
Sep 15, 2025
-
Plastic Wire Coating
Sep 15, 2025
-
North East Farming
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 10000 / 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.