100 / 8
stanleys
Sep 12, 2025 · 6 min read
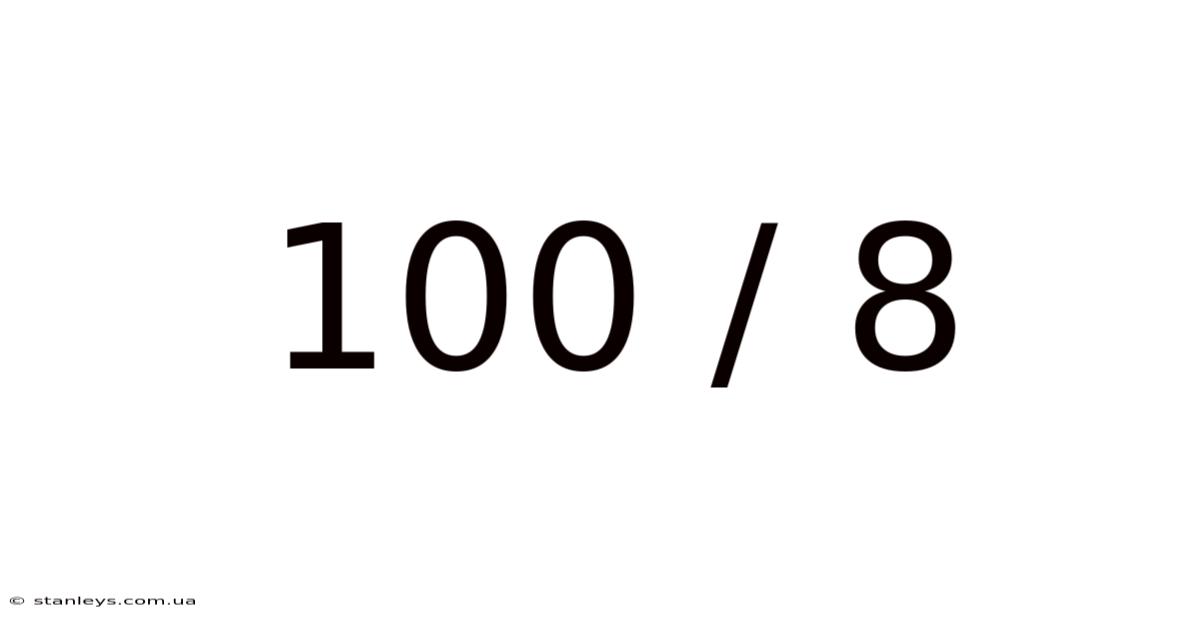
Table of Contents
Decoding 100/8: A Deep Dive into Division and its Applications
This article explores the seemingly simple division problem 100/8, delving far beyond the immediate answer. We'll uncover the fundamental principles of division, explore various methods of solving it, examine its practical applications across different fields, and even touch upon the historical context of division. Understanding 100/8 isn't just about finding the quotient; it's about grasping the underlying mathematical concepts and their real-world significance.
Introduction: What Does 100/8 Really Mean?
The expression 100/8 represents the process of dividing 100 into 8 equal parts. It asks the question: "How many times does 8 fit into 100?" The answer, as we'll soon see, is not a whole number, highlighting the importance of understanding remainders and decimals in division. This seemingly basic calculation forms the bedrock of many complex mathematical operations and practical applications. This article will equip you with not just the solution but a profound understanding of the concepts involved.
Methods of Solving 100/8
There are several ways to solve 100/8, each offering a unique perspective on the division process.
-
Long Division: This traditional method provides a step-by-step approach, perfect for understanding the mechanics of division.
- Set up the problem: 8 | 100
- Divide 8 into 10: 8 goes into 10 once (1), with a remainder of 2.
- Bring down the next digit (0): The remainder 2 becomes 20.
- Divide 8 into 20: 8 goes into 20 twice (2), with a remainder of 4.
- Since there are no more digits to bring down, the 4 is the remainder.
- The answer is 12 with a remainder of 4, often written as 12 R 4.
-
Short Division: This method is a more concise version of long division, suitable for simpler problems. It involves mental calculations and is faster once mastered. You would mentally divide 8 into 10 and 8 into 20 to arrive at the same 12 R 4.
-
Using Fractions: We can express 100/8 as the fraction 100/8. This fraction can be simplified by finding the greatest common divisor (GCD) of 100 and 8, which is 4. Simplifying, we get 25/2. This fraction can then be converted to a decimal by performing the division: 25 ÷ 2 = 12.5.
-
Using a Calculator: The simplest method is using a calculator. Inputting 100 ÷ 8 directly yields the decimal answer 12.5. While convenient, this method doesn't offer the same understanding of the underlying process as the other methods.
Understanding Remainders and Decimals
The long division method reveals a remainder of 4. This means that when we divide 100 into 8 equal parts, we get 12 complete parts and 4 remaining units. The fractional representation (25/2) and the decimal representation (12.5) show that the remaining 4 units can be expressed as a fraction (4/8 = 1/2) or a decimal (0.5).
Real-World Applications of Division: Examples using 100/8
The seemingly simple 100/8 problem has surprisingly numerous applications across diverse fields. Here are some examples:
-
Sharing Resources: Imagine you have 100 candies to distribute equally among 8 friends. Each friend receives 12 candies, and you have 4 candies left over.
-
Unit Pricing: If a pack of 8 pencils costs $100, the price of one pencil is $12.50 ($100/8 = $12.50).
-
Average Calculation: Suppose 8 students scored a total of 100 points on a test. Their average score is 12.5 points (100/8 = 12.5).
-
Measurement Conversion: Imagine converting 100 centimeters to groups of 8 centimeters each. You'll have 12.5 groups.
-
Engineering and Construction: Dividing resources or calculating measurements for construction projects frequently involves similar divisions. For example, distributing 100 meters of wire among 8 sections requires a calculation of 100/8 = 12.5 meters per section.
-
Data Analysis and Statistics: Calculating averages, rates, and proportions often involves division, making it a fundamental tool in data analysis. The 100/8 example could represent a small scale data point in a larger dataset.
-
Computer Science: In computer programming, resource allocation and data manipulation often necessitate division. For instance, distributing 100 processing tasks across 8 cores would require the same mathematical operation.
-
Finance: Dividing profits or expenses among shareholders or calculating interest rates can use division calculations that follow a similar principle to 100/8.
Exploring Deeper Mathematical Concepts
The problem 100/8 provides a gateway to exploring more complex mathematical concepts:
-
Euclidean Division: This theorem formalizes the concept of division with a remainder. For any integers a (dividend) and b (divisor) where b ≠ 0, there exist unique integers q (quotient) and r (remainder) such that a = bq + r, and 0 ≤ r < |b|. In our case, a = 100, b = 8, q = 12, and r = 4.
-
Modular Arithmetic: The remainder in division (4 in this case) is crucial in modular arithmetic. We can say that 100 is congruent to 4 modulo 8, written as 100 ≡ 4 (mod 8). This is fundamental in cryptography and other areas of mathematics.
-
Decimal Representation: Converting the remainder into a decimal (0.5) illustrates how we represent numbers using base 10. Understanding decimal representation is fundamental to many mathematical and scientific applications.
-
Rational Numbers: The fraction 25/2 shows that 12.5 is a rational number – a number that can be expressed as a fraction of two integers. Rational numbers form a significant subset of the real number system.
Historical Context of Division
The concept of division has been around for millennia. Ancient civilizations like the Babylonians and Egyptians used various methods for division, often involving sophisticated techniques for handling remainders and fractions. The development of modern notation and algorithms for division is a testament to the evolution of mathematical thinking over centuries.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to solve 100/8?
- A: Using a calculator is the quickest method, but long division provides a deeper understanding of the process.
-
Q: What does the remainder represent?
- A: The remainder represents the amount left over after dividing the dividend into equal parts based on the divisor.
-
Q: Can 100/8 be expressed as a fraction?
- A: Yes, it can be expressed as 100/8, which simplifies to 25/2.
-
Q: What is the decimal equivalent of 100/8?
- A: The decimal equivalent is 12.5.
-
Q: Why is understanding remainders important?
- A: Understanding remainders is essential in various applications, including resource allocation, measurement conversions, and modular arithmetic.
Conclusion: Beyond the Numbers
The seemingly simple division problem 100/8 unveils a wealth of mathematical concepts and practical applications. From the fundamental principles of long division to the broader implications of remainders and decimals, this seemingly straightforward calculation provides a foundation for understanding more complex mathematical ideas and their real-world relevance. This deep dive has demonstrated that the true value lies not just in the answer (12.5), but in the comprehensive understanding of the process and its various implications across diverse fields. By exploring various methods, understanding the historical context, and appreciating the real-world applications, we’ve moved beyond a simple calculation to a richer appreciation of the power and versatility of division.
Latest Posts
Latest Posts
-
64 8kg To Pounds
Sep 12, 2025
-
30 Of 900
Sep 12, 2025
-
Squoval Nail Shape
Sep 12, 2025
-
Factorise 8x 6
Sep 12, 2025
-
63 3kg In Stone
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 100 / 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.