10 Of 450
stanleys
Sep 14, 2025 · 6 min read
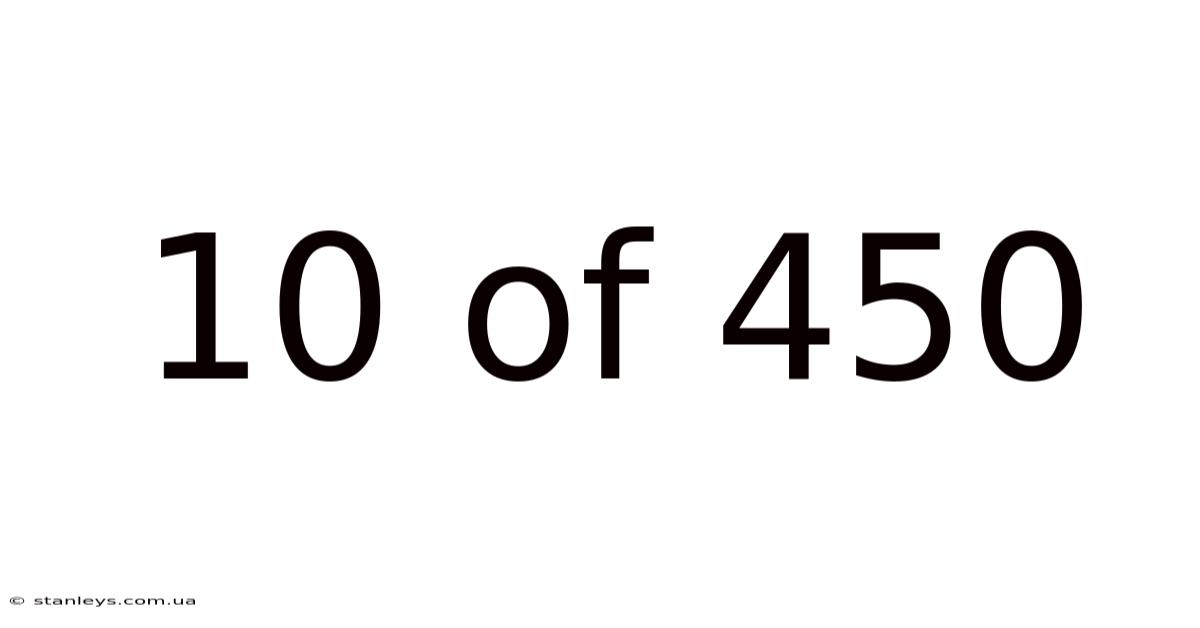
Table of Contents
Decoding the Mystery: Understanding the Fraction 10/450 and its Applications
The seemingly simple fraction 10/450 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a deeper understanding of fundamental mathematical concepts and their real-world applications. This article will delve into the intricacies of 10/450, exploring its simplification, decimal equivalent, percentage representation, and practical uses across different fields. We'll also address common misconceptions and answer frequently asked questions to provide a comprehensive overview.
Introduction: Unveiling the Simplicity Within Complexity
The fraction 10/450 represents a part-to-whole relationship. It signifies 10 units out of a total of 450 units. While this might seem straightforward, its inherent simplicity allows us to explore several key mathematical concepts and their practical relevance. By simplifying the fraction, converting it to a decimal and percentage, and understanding its applications, we gain a comprehensive understanding of its significance. This understanding is crucial not only for basic arithmetic but also for more advanced concepts in algebra, geometry, and even statistics.
Step-by-Step Simplification: Finding the Lowest Terms
The first step in understanding 10/450 is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (10) and the denominator (450). The GCD is the largest number that divides both numbers without leaving a remainder.
-
Finding the GCD: Both 10 and 450 are divisible by 10.
-
Dividing both Numerator and Denominator: Dividing both the numerator and the denominator by 10, we get:
10 ÷ 10 = 1 450 ÷ 10 = 45
Therefore, the simplified fraction is 1/45. This simplified form is much easier to work with and provides a clearer representation of the part-to-whole relationship.
Decimal Representation: Expressing the Fraction as a Decimal Number
Converting the simplified fraction 1/45 to a decimal involves dividing the numerator (1) by the denominator (45). This can be done using long division or a calculator.
-
Performing the Division: 1 ÷ 45 = 0.02222...
-
Identifying the Repeating Decimal: The result is a repeating decimal, specifically 0.02222..., where the digit '2' repeats infinitely. This can be represented as 0.02̅ (the bar indicates the repeating digit).
The decimal representation provides a different perspective on the fraction, expressing it as a value between 0 and 1. This form is particularly useful in applications involving calculations and comparisons.
Percentage Representation: Expressing the Fraction as a Percentage
Converting the fraction to a percentage provides another way of representing the part-to-whole relationship. To convert a decimal to a percentage, we multiply it by 100 and add the percentage symbol.
-
Converting the Decimal to a Percentage: 0.02̅ × 100 ≈ 2.22%
-
Rounding: Since the decimal is repeating, we might round the percentage to a specific number of decimal places, for example, 2.22%.
The percentage representation makes it easier to visualize the relative size of the fraction compared to the whole. For instance, 10/450 or 1/45 represents approximately 2.22% of the total.
Practical Applications Across Diverse Fields
The seemingly simple fraction 10/450, or its simplified form 1/45, has surprising applications in various fields:
-
Statistics and Probability: In statistical analysis, this fraction could represent the probability of a specific event occurring. For example, if there are 45 possible outcomes, and only one is favorable, the probability of that favorable outcome occurring is 1/45.
-
Business and Finance: This fraction can be used in various business calculations, such as calculating profit margins, market share, or the proportion of a specific product sold compared to the total sales.
-
Engineering and Design: In engineering and design, fractions are used extensively in scaling and proportioning. 1/45 could represent a specific scaling factor in blueprints or models.
-
Cooking and Baking: Fractions are essential in recipes, where precise measurements are crucial. 1/45 might represent a small portion of an ingredient in a recipe.
-
Science: In various scientific experiments and calculations, fractions are crucial for representing ratios, concentrations, and proportions.
Illustrative Examples: Real-World Scenarios
Let's explore a few real-world examples showcasing the practical applications of 10/450:
-
Scenario 1: Quality Control: In a manufacturing process, 10 out of 450 products were found to be defective. The fraction 10/450 (simplified to 1/45) represents the defect rate. This information is crucial for improving the manufacturing process.
-
Scenario 2: Survey Results: In a survey of 450 individuals, 10 responded positively to a specific question. The fraction 10/450 (1/45) represents the proportion of positive responses.
-
Scenario 3: Recipe Scaling: A recipe calls for 450 grams of flour. If you only need 1/45 of the recipe, you would use 10 grams of flour (450 grams / 45 = 10 grams).
Addressing Common Misconceptions
Many people struggle with fractions, often due to misunderstandings. Some common misconceptions surrounding 10/450 include:
-
Difficulty in Simplification: Many struggle to find the greatest common divisor (GCD) and simplify the fraction correctly. This can be overcome with practice and understanding of prime factorization.
-
Decimal Conversion Challenges: Converting a fraction to a decimal can be challenging, especially with repeating decimals. Understanding long division and using calculators effectively can help overcome this hurdle.
Frequently Asked Questions (FAQs)
-
Q: What is the simplest form of 10/450?
- A: The simplest form is 1/45.
-
Q: What is the decimal equivalent of 10/450?
- A: The decimal equivalent is approximately 0.02̅ (repeating decimal).
-
Q: What is the percentage equivalent of 10/450?
- A: The percentage equivalent is approximately 2.22%.
-
Q: How can I simplify fractions effectively?
- A: Find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD. Prime factorization can help find the GCD.
-
Q: What are some real-world applications of this type of fraction?
- A: Numerous applications exist in statistics, probability, finance, engineering, cooking, and science, representing ratios, proportions, probabilities, or scaling factors.
Conclusion: Embracing the Power of Simple Fractions
The fraction 10/450, seemingly insignificant at first glance, offers a powerful illustration of fundamental mathematical concepts and their wide-ranging applications. By understanding its simplification, decimal and percentage equivalents, and practical uses, we gain valuable insights into the world of mathematics and its relevance to various fields. Mastering fractions is a crucial stepping stone towards advanced mathematical concepts, enabling a deeper understanding and appreciation of the world around us. The seemingly simple fraction 10/450 is a testament to the power of foundational mathematical knowledge and its ability to solve real-world problems across diverse disciplines. Therefore, it's essential to develop a strong grasp of these fundamental concepts.
Latest Posts
Latest Posts
-
Cleaning Of Floors
Sep 14, 2025
-
55miles In Km
Sep 14, 2025
-
Poison Tree Emoji
Sep 14, 2025
-
80z In Ml
Sep 14, 2025
-
Allison Breakfast Club
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.