10 Of 12.00
stanleys
Sep 10, 2025 · 6 min read
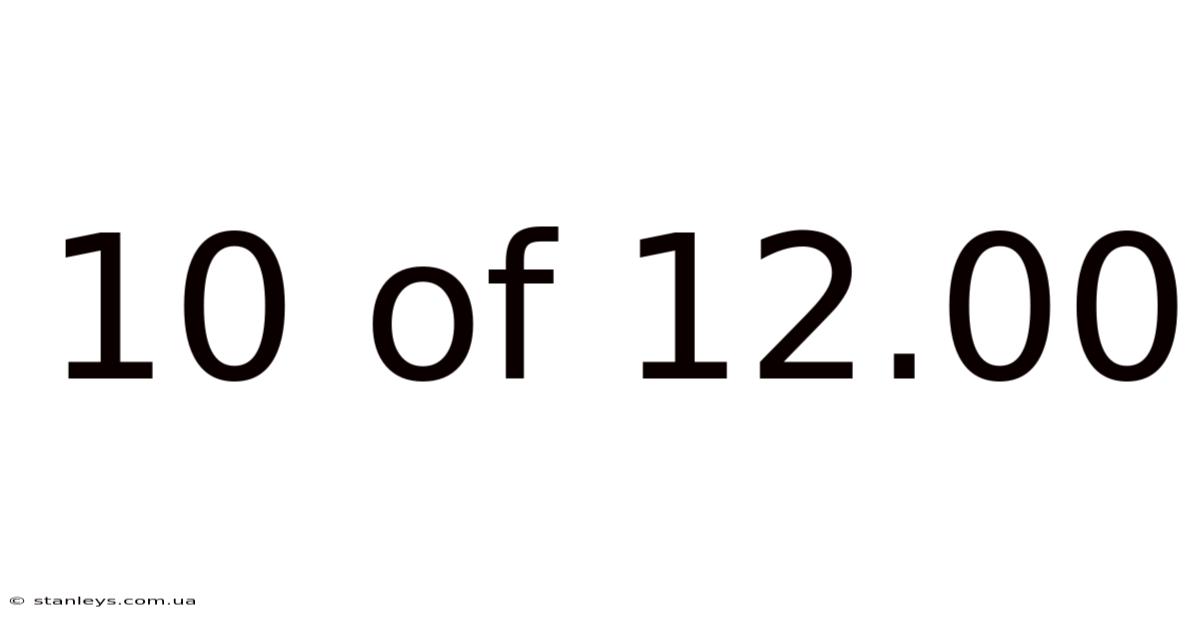
Table of Contents
Decoding 10 of 12.00: Understanding Time, Fractions, and Ratios
Have you ever encountered the notation "10 of 12.00" and wondered what it means? This seemingly simple phrase can represent various concepts, depending on the context. This article will delve into the different interpretations of "10 of 12.00," exploring its meaning in relation to time, fractions, ratios, and percentages, ensuring a comprehensive understanding for all levels of comprehension. We'll also cover some common scenarios where you might see this notation.
Understanding the Components
Before we dive into the interpretations, let's break down the components of "10 of 12.00":
- 10: This represents a specific quantity or value.
- of: This indicates a relationship, often signifying a part of a whole.
- 12.00: This represents the total quantity or whole. The ".00" typically implies precision to the hundredth, often seen in timekeeping or monetary values.
Interpretation 1: Time
In a time-related context, "10 of 12.00" can represent 10:00 AM or PM on a 12-hour clock system. The "12.00" signifies the 12-hour cycle, and "10" represents the hour. The context is crucial here; without further information, it's impossible to definitively state whether it's AM or PM.
- Example: A schedule might indicate "Meeting at 10 of 12.00," meaning the meeting is scheduled for 10:00 AM or 10:00 PM. Clear communication is vital in such instances to avoid confusion.
Interpretation 2: Fraction and Percentage
Mathematically, "10 of 12.00" can be interpreted as a fraction: 10/12.00. This fraction can be simplified to 5/6. To express this as a percentage, we perform the calculation: (10/12) * 100% = 83.33%. Therefore, "10 of 12.00" represents approximately 83.33% of the total.
- Example: If you completed 10 out of 12 tasks, you've completed 10/12 or 83.33% of the workload. This is a common way to express progress towards a goal. Understanding percentages allows you to readily grasp your progress relative to the total.
Interpretation 3: Ratio
"10 of 12.00" can also be viewed as a ratio, representing a relationship between two quantities. The ratio is 10:12, which simplifies to 5:6. This indicates that for every 5 units of one quantity, there are 6 units of another.
- Example: If a recipe calls for a ratio of 10 parts flour to 12 parts water, this can be simplified to a 5:6 ratio, making it easier to adjust the recipe for larger or smaller batches. Ratios are fundamental in various fields, including cooking, engineering, and science.
Understanding the Context: Crucial for Accurate Interpretation
The accurate interpretation of "10 of 12.00" entirely depends on its context. Without knowing the domain or field where this notation is used, it is impossible to provide a single definitive meaning. This highlights the importance of clear communication and the use of unambiguous language.
Expanding on Fractions and Percentages: A Deeper Dive
The fractional representation, 10/12, highlights the concept of parts of a whole. This is a fundamental concept in mathematics and is encountered across various applications. Understanding fractions allows us to divide a whole into smaller parts and express these parts as fractions. The denominator (12 in this case) indicates the total number of parts, and the numerator (10) indicates the number of parts we are considering.
Converting fractions to percentages provides a way to express fractional quantities as a proportion of 100. This helps in easier comparison and understanding. For instance, 83.33% gives a clearer picture of the progress than simply stating 10/12. This percentage representation is universally understood and widely used across various fields, making it a powerful tool for communication and data analysis.
Expanding on Ratios: Applications and Importance
Ratios, like fractions, are essential mathematical concepts that describe the relative sizes of two or more quantities. Unlike fractions, which represent a part of a whole, ratios compare two or more quantities. In the case of "10 of 12.00," the ratio is 10:12 or 5:6, showing a comparison between two quantities.
Ratios are critical in several fields:
- Cooking: Recipes often use ratios to maintain proportions of ingredients. A 1:1 ratio of sugar to flour, for example, means equal amounts.
- Engineering: Ratios are used to determine the strength of materials, scale models, and many other engineering applications.
- Science: Ratios are fundamental in various scientific calculations, such as concentration ratios in chemistry or population ratios in ecology.
- Finance: Ratios are used to analyze financial statements, assessing profitability, liquidity, and leverage of a company.
Mastering ratios helps improve analytical skills and problem-solving capabilities. The ability to simplify and work with ratios is crucial for various real-world applications.
Common Scenarios Where "10 of 12.00" Might Appear
- Progress Tracking: Project management software or reports might display progress as "10 of 12 tasks completed."
- Inventory Management: A warehouse might have "10 of 12.00 units in stock."
- Scheduling: As mentioned previously, time scheduling could use this format.
- Testing and Evaluation: A test might have "10 of 12.00 questions answered correctly."
- Data Analysis: Data sets might present information in this ratio format for easier comparison and interpretation.
Frequently Asked Questions (FAQ)
Q: What if the "12.00" was a different number? How would the interpretation change?
A: The interpretation would change proportionally. If it was "10 of 15.00," the fraction would be 10/15 (simplified to 2/3), the percentage would be approximately 66.67%, and the ratio would be 10:15 or 2:3. The core concepts—fractions, percentages, and ratios—remain the same, but the numerical values would change accordingly.
Q: Is it necessary to use the ".00" after the 12?
A: The ".00" generally implies precision, often used in contexts demanding accuracy, such as financial statements or precise timekeeping. In less precise contexts, it might be omitted. "10 of 12" would convey the same core meaning, but the lack of ".00" might suggest a less precise measurement.
Q: How can I improve my understanding of fractions, percentages, and ratios?
A: Practice is key. Work through various examples, solve problems, and seek out resources such as online tutorials, educational websites, or textbooks. Start with simple examples and gradually move towards more complex scenarios. Understanding the underlying concepts and their applications is crucial for effective problem-solving.
Conclusion
"10 of 12.00" is a versatile notation that can represent different concepts depending on context. Understanding its possible interpretations—time, fraction, percentage, and ratio—is essential for accurate comprehension and effective communication. By grasping the fundamentals of fractions, percentages, and ratios, you'll equip yourself with valuable analytical skills applicable across various fields. Remember, always consider the context to accurately interpret the meaning of "10 of 12.00" or similar notations. The ability to decode such seemingly simple phrases is a testament to strong analytical and mathematical skills, making you a more effective problem-solver and communicator.
Latest Posts
Latest Posts
-
18cms In Inches
Sep 10, 2025
-
18 5 Of 982
Sep 10, 2025
-
92km To Miles
Sep 10, 2025
-
0 9 In Percentage
Sep 10, 2025
-
Singapore Olympic Games
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 12.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.