10 Of 1100
stanleys
Sep 21, 2025 · 6 min read
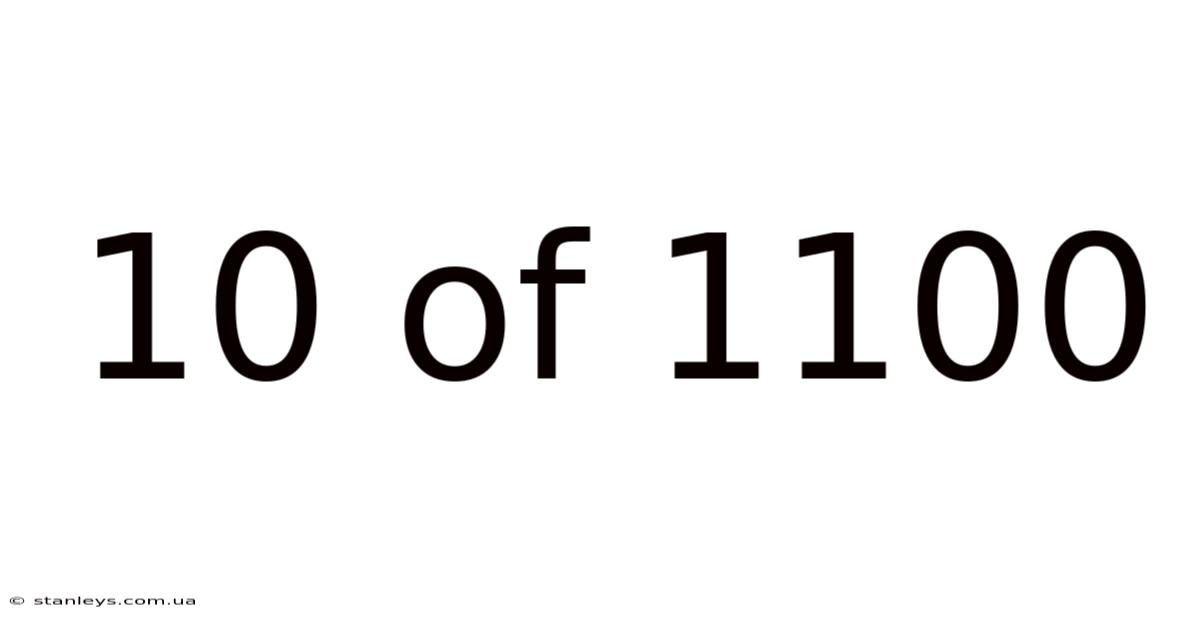
Table of Contents
Decoding 10 out of 1100: Understanding Proportions, Percentages, and their Applications
Understanding fractions, proportions, and percentages is fundamental to navigating the world around us. Whether it's calculating discounts at the mall, understanding election results, or interpreting scientific data, the ability to interpret and utilize these mathematical concepts is crucial. This article delves into the meaning of "10 out of 1100," exploring its representation as a fraction, a decimal, and a percentage, and expanding on its broader applications in various fields. We'll also tackle common misconceptions and address frequently asked questions.
Introduction: The Significance of Ratios and Proportions
The statement "10 out of 1100" represents a ratio – a comparison of two quantities. This ratio can be expressed in several ways, each offering a different perspective on the relationship between the two numbers. Understanding these different representations is key to effective interpretation and application. We'll break down this specific ratio and explore how it's used in real-world scenarios, providing practical examples to solidify your understanding.
Representing 10 out of 1100: Different Formats
1. Fraction: The most direct representation of "10 out of 1100" is the fraction 10/1100. This fraction can be simplified by dividing both the numerator (10) and the denominator (1100) by their greatest common divisor, which is 10. This simplifies the fraction to 1/110.
2. Decimal: To convert the fraction 1/110 to a decimal, we perform the division: 1 ÷ 110 ≈ 0.0090909... This is a recurring decimal, meaning the sequence "09" repeats infinitely. For practical purposes, we often round this to a certain number of decimal places, such as 0.0091.
3. Percentage: A percentage represents a fraction out of 100. To express 1/110 as a percentage, we multiply the decimal equivalent (approximately 0.00909) by 100: 0.00909 × 100 ≈ 0.909%. Again, for practicality, we might round this to 0.91%.
Therefore, "10 out of 1100" can be represented as:
- Fraction: 10/1100 = 1/110
- Decimal: Approximately 0.0091
- Percentage: Approximately 0.91%
Understanding the Context: Real-World Applications
The interpretation and significance of "10 out of 1100" heavily depend on the context. Consider these examples:
-
Survey Results: If 10 out of 1100 respondents to a survey answered "yes" to a particular question, this represents a relatively low percentage (0.91%) of positive responses. This could indicate a low level of agreement or support for the topic in question.
-
Quality Control: In a manufacturing process, if 10 out of 1100 items are found to be defective, this represents a defect rate of approximately 0.91%. While seemingly low, depending on the industry and the cost of defects, this might still be considered unacceptable and warrant investigation into the manufacturing process.
-
Scientific Experiments: In scientific research, a small ratio like 10 out of 1100 might represent a statistically insignificant result, depending on the experiment's design and the level of statistical significance being sought. Larger sample sizes are often required to draw meaningful conclusions.
-
Financial Markets: In financial analysis, 10 out of 1100 successful trades might reflect a success rate of 0.91%, indicating that a significant portion of trades were unsuccessful. This would suggest a need to review and improve the trading strategy.
Beyond the Numbers: Interpreting Proportions and Percentages Effectively
Interpreting proportions and percentages accurately involves more than just calculating the numerical values. It requires understanding the context and considering the potential implications. Here are some important considerations:
-
Sample Size: The size of the sample is crucial. A small sample size can lead to misleading results. For instance, 10 out of 100 (10%) is a much higher proportion than 10 out of 1100 (0.91%).
-
Statistical Significance: In statistical analysis, determining if a result is statistically significant is essential before drawing conclusions. This involves considering factors like the sample size, the variability of the data, and the desired level of confidence.
-
Margin of Error: When dealing with surveys or estimations, there's always a margin of error. This reflects the uncertainty inherent in the data and should be considered when interpreting the results.
-
Underlying Causes: Understanding the why behind the numbers is just as important as understanding the numbers themselves. For example, if 10 out of 1100 products are defective, investigating the root cause of the defect is crucial to prevent future occurrences.
Advanced Applications: Proportions in More Complex Scenarios
Proportions and percentages are fundamental to many advanced mathematical concepts and applications:
-
Probability: Probability calculations frequently involve ratios and proportions. For example, the probability of selecting a defective item from a batch can be calculated as the ratio of defective items to the total number of items.
-
Rate of Change: Percentages are frequently used to express rates of change, such as the growth rate of a population or the change in stock prices.
-
Financial Modeling: Financial models heavily rely on proportions and percentages to forecast future performance, assess risk, and make investment decisions.
-
Epidemiology: In epidemiology, proportions are used to track the spread of diseases, to calculate incidence rates, and to assess the effectiveness of public health interventions.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage from a fraction?
A: To convert a fraction to a percentage, divide the numerator by the denominator, then multiply the result by 100%. For example, 1/110 = 0.00909... Multiplying by 100 gives approximately 0.91%.
Q: What is the difference between a ratio and a proportion?
A: A ratio is a comparison of two quantities. A proportion is a statement that two ratios are equal. For example, 10/1100 is a ratio. The statement 10/1100 = 1/110 is a proportion.
Q: How can I improve my understanding of proportions and percentages?
A: Practice is key! Work through various examples, solve problems, and try to apply these concepts to real-world situations. Using online resources, textbooks, or educational videos can also be helpful.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and compare. It also makes calculations simpler and reduces the likelihood of errors.
Q: Are there any online tools or calculators that can help me with these calculations?
A: Yes, many online calculators are available to perform these calculations quickly and accurately. Search online for "fraction to percentage calculator" or "ratio calculator" to find helpful tools. (Note: As per the instructions, I cannot provide external links.)
Conclusion: The Power of Understanding Proportions
The seemingly simple ratio of "10 out of 1100" showcases the power and versatility of understanding proportions, percentages, and their applications across numerous fields. By mastering these fundamental concepts, you equip yourself with essential tools for critical thinking, problem-solving, and informed decision-making in various aspects of life. Remember that the numerical value alone is not sufficient; context, statistical significance, and a deeper understanding of the underlying factors are crucial for accurate and meaningful interpretation. Continued practice and exploration will further solidify your grasp of these fundamental mathematical tools.
Latest Posts
Related Post
Thank you for visiting our website which covers about 10 Of 1100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.