10 Of 1000
stanleys
Sep 12, 2025 · 5 min read
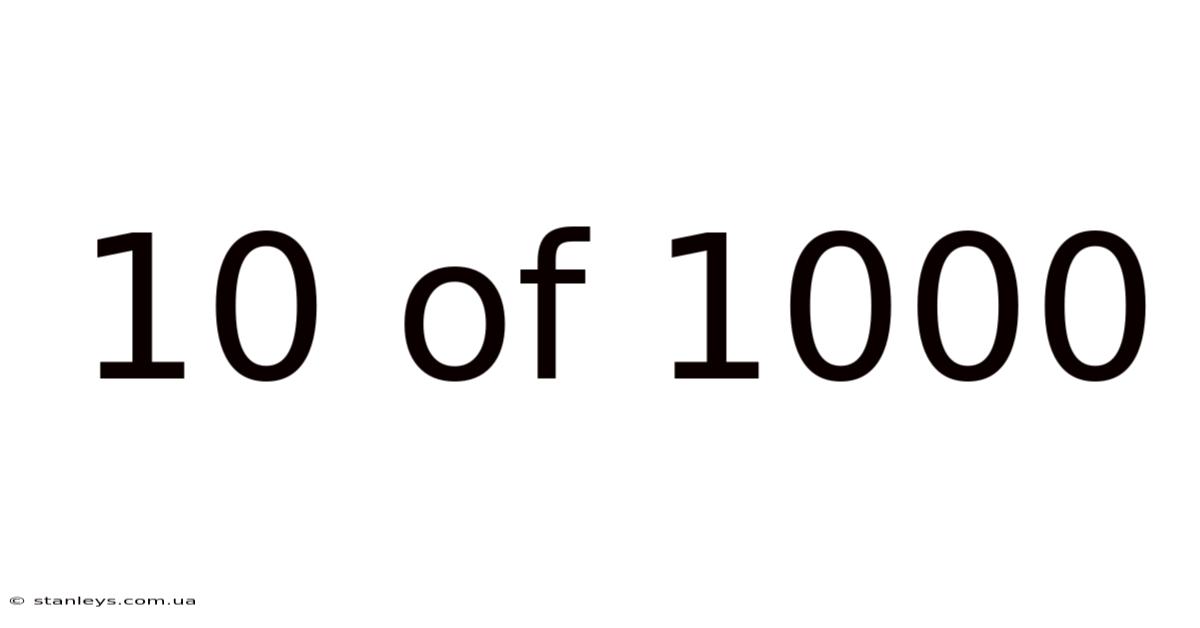
Table of Contents
Decoding 10/1000: Understanding the Significance of a Thousandth
The seemingly simple fraction 10/1000, or its decimal equivalent 0.01, holds surprising depth and significance across various fields. Understanding its implications requires exploring its representation in different contexts, from basic mathematics to advanced scientific applications. This article delves into the multifaceted nature of 10/1000, unpacking its meaning and exploring its relevance in diverse areas. We will examine its role in percentages, probability, scientific notation, and more, providing a comprehensive understanding for readers of all levels.
Understanding the Basics: Fractions, Decimals, and Percentages
At its core, 10/1000 is a fraction – a representation of a part of a whole. The numerator (10) indicates the number of parts we are considering, while the denominator (1000) represents the total number of equal parts making up the whole. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10. This simplification results in 1/100.
This simplification highlights the inherent relationship between fractions and decimals. 1/100 is easily converted to a decimal by performing the division: 1 divided by 100 equals 0.01. This decimal representation is particularly useful in many applications, offering a concise and easily comparable format.
Furthermore, 10/1000, or 1/100, also translates directly to a percentage. A percentage represents a fraction of 100, so 1/100 is equivalent to 1%. This means that 10/1000 represents 1% of a whole. This percentage representation is widely used to express proportions and probabilities in everyday life and various professional contexts.
Applications of 10/1000 in Different Fields
The significance of 10/1000 extends far beyond its basic mathematical representation. Its small magnitude makes it particularly relevant in scenarios where precision and minute changes are crucial. Let's explore some key applications:
1. Finance and Economics:
In finance, 0.01 or 1% often represents a small change in interest rates, stock prices, or inflation. While seemingly insignificant individually, these small changes can accumulate over time and have substantial effects on investment returns, loan payments, and overall economic trends. Analyzing market fluctuations often involves examining changes in the order of 0.01%, highlighting the importance of understanding this seemingly minor value.
2. Science and Engineering:
In scientific measurements, 0.01 or 1% can represent a crucial level of accuracy. For example, in chemical analysis, a 1% error in a measurement can significantly impact the results of an experiment. Similarly, in engineering, tolerances and precision often involve measurements down to 0.01 units, ensuring the proper functioning of complex systems. Consider scenarios involving the calibration of instruments – the accuracy needed frequently necessitates dealing with values of 0.01 units.
3. Probability and Statistics:
In probability, 10/1000 or 1% can represent a small probability of an event occurring. Understanding these small probabilities is vital in risk assessment and decision-making. For instance, a 1% chance of a specific component failing in a system might be deemed acceptable, while a higher probability might necessitate design changes or redundancy measures. Statistical analysis frequently involves dealing with percentages and probabilities that include values like 1% or 0.01, requiring careful interpretation.
4. Computer Science:
In computer science, representing data often involves dealing with decimal or binary fractions. 0.01 can represent a small change in a variable or a fractional part of a larger value. In image processing, for example, color values are often expressed using decimal values that can include precision up to 0.01 units. Similarly, many algorithms involve computations with decimal values, and understanding their precision is essential.
5. Environmental Science:
Environmental science frequently involves the analysis of tiny changes in environmental parameters. For example, a 1% change in the concentration of a pollutant in a water body can have significant ecological consequences. Understanding these minute changes requires a clear grasp of fractions and decimal representations, including 0.01 and its equivalent values.
Scientific Notation and 10/1000
The representation of 10/1000 can also be simplified using scientific notation. Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10, and 'b' is an integer representing the power of 10. In this case, 0.01 can be expressed as 1 x 10<sup>-2</sup>.
This scientific notation is particularly useful when dealing with extremely small or large numbers, providing a concise and convenient representation. Its use is prevalent across scientific and engineering fields, improving readability and facilitating calculations involving magnitudes varying across several orders.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 10/1000?
A: The simplest form of 10/1000 is 1/100. This is obtained by dividing both the numerator and denominator by their greatest common divisor, which is 10.
Q: How do I convert 10/1000 to a percentage?
A: To convert 10/1000 to a percentage, first simplify the fraction to 1/100. Since a percentage represents parts per hundred, 1/100 is directly equivalent to 1%.
Q: What is the decimal equivalent of 10/1000?
A: The decimal equivalent of 10/1000 is 0.01. This is found by performing the division: 10 divided by 1000.
Q: Why is understanding 10/1000 important?
A: Understanding 10/1000 is important because it represents a small but significant proportion in many contexts. It's crucial for precision in scientific measurements, for analyzing small changes in financial markets, and for understanding probabilities in various scenarios.
Q: Can 10/1000 be expressed in scientific notation?
A: Yes, 10/1000 (or 0.01) can be expressed in scientific notation as 1 x 10<sup>-2</sup>.
Conclusion: The Unsung Significance of a Small Fraction
While seemingly insignificant at first glance, 10/1000, or 0.01, carries substantial weight across numerous disciplines. Its understanding is not merely a matter of basic arithmetic; it’s about grasping its implications in precision measurements, probability assessments, financial analyses, and more. This seemingly simple fraction underscores the importance of understanding small changes and their cumulative effects. From the minute adjustments in scientific experiments to the subtle shifts in economic indicators, mastering the concept of 10/1000 unlocks a deeper understanding of the world around us. Its seemingly small magnitude belies a significant role in numerous fields, making it a concept worth exploring and understanding in detail.
Latest Posts
Latest Posts
-
76km In Miles
Sep 12, 2025
-
Stock Control System
Sep 12, 2025
-
600kg In Stone
Sep 12, 2025
-
Mariana Trench Pictures
Sep 12, 2025
-
Red Dress Red
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.