10.00 X 20
stanleys
Sep 14, 2025 · 7 min read
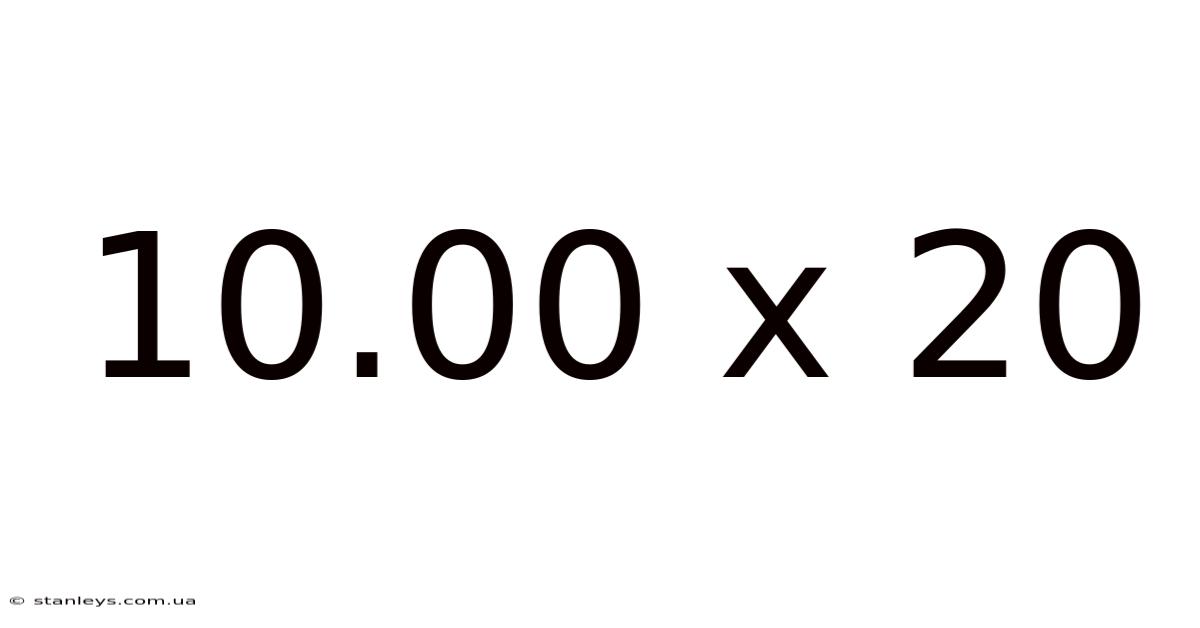
Table of Contents
Decoding 10.00 x 20: Exploring Multiplication, its Applications, and Beyond
This article delves into the seemingly simple calculation of 10.00 x 20, unpacking the underlying principles of multiplication, exploring its diverse applications across various fields, and extending the concept to broader mathematical ideas. We'll move beyond the immediate answer to understand the "why" behind the calculation and how it connects to more complex mathematical concepts. This exploration is suitable for students seeking a deeper understanding of basic arithmetic, as well as anyone curious about the practical implications and theoretical foundations of multiplication.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a streamlined way of performing repeated addition. The equation 10.00 x 20 can be interpreted as adding 10.00 twenty times: 10.00 + 10.00 + 10.00 + ... (repeated 20 times). This fundamental understanding is crucial, particularly for grasping the concept of multiplication with larger numbers or fractions. While calculators quickly provide the answer (200), comprehending the underlying principle lays the foundation for more advanced mathematical operations.
The Calculation: 10.00 x 20 = 200
The calculation itself is straightforward: 10.00 multiplied by 20 equals 200. The presence of the decimal point in 10.00 doesn't alter the core multiplication process. It simply indicates precision to two decimal places, implying that the number is exactly 10 and not an approximation. This precision is important in many practical applications, as we'll discuss later.
Practical Applications: Where We Use Multiplication Daily
Multiplication isn't confined to the classroom; it's a fundamental tool used extensively in daily life and across various professions. Here are a few examples:
- Shopping: Calculating the total cost of multiple items. If you buy 20 apples at $10.00 per dozen, you'd need to adjust the calculation accordingly, demonstrating the need for adapting multiplication to various scenarios. (Note: this requires a slightly more complex calculation involving unit price adjustments).
- Finance: Calculating interest earned on savings, determining total loan payments, or understanding stock market gains. Understanding multiplication is crucial for managing personal finances effectively.
- Construction & Engineering: Calculating the quantity of materials needed for a project, determining the dimensions of structures, and more. Precision in multiplication is paramount in ensuring structural integrity and project success.
- Cooking & Baking: Scaling up or down recipes. A recipe that calls for 10 grams of an ingredient and needs to be multiplied for 20 servings requires accurate calculation.
- Data Analysis: Working with datasets, manipulating spreadsheets, and performing statistical calculations rely heavily on multiplication. Data scientists and analysts regularly use this operation to derive insights.
- Travel: Calculating distances, fuel consumption, travel time, and cost estimations.
These examples highlight the pervasive nature of multiplication in everyday life, underscoring its practical importance beyond the theoretical realm.
Expanding the Concept: Beyond Basic Multiplication
The simplicity of 10.00 x 20 allows us to explore more complex mathematical concepts.
- Distributive Property: This property allows us to break down complex multiplication problems into smaller, more manageable ones. For instance, 10.00 x 20 can be seen as 10.00 x (10 + 10), which simplifies to (10.00 x 10) + (10.00 x 10) = 100 + 100 = 200. This demonstrates the versatility of multiplication and its connection to other algebraic principles.
- Commutative Property: This property states that the order of numbers in multiplication doesn't affect the result. Therefore, 10.00 x 20 is equal to 20 x 10.00. This seemingly simple observation helps simplify calculations and highlights the symmetric nature of multiplication.
- Associative Property: This property involves the grouping of numbers in multiplication. While less directly applicable to 10.00 x 20, it becomes important when dealing with three or more numbers: (a x b) x c = a x (b x c). Understanding this property enhances the ability to efficiently solve more complex problems.
- Multiplication with Fractions and Decimals: Expanding beyond whole numbers, we can apply multiplication to fractions and decimals. For instance, 10.00 x 20.5 requires understanding how to multiply numbers with decimal places. This necessitates a clear understanding of place value and the rules for multiplying decimals.
- Algebraic Applications: Multiplication forms the basis of many algebraic equations and manipulations. Variables represent unknown quantities, and multiplication operations become essential for solving for those variables. This further underscores the interconnectedness of arithmetic and algebra.
- Exponents and Powers: Multiplication is the foundation of exponents (or powers). 10.00 x 10.00 can be represented as 10.00², illustrating the relationship between repeated multiplication and exponential notation. This leads into understanding exponential growth and decay, concepts with significant applications in various fields like finance and biology.
Understanding Place Value and Decimal Points
The presence of the decimal point in 10.00 highlights the importance of place value. Each digit in a number has a specific value based on its position. The 0 to the right of the decimal point represents tenths, and the next 0 represents hundredths. In this case, the zeros after the decimal point simply reinforce the precision of the number 10.
The Significance of Zero
The number zero plays a crucial role in multiplication. Multiplying any number by zero results in zero (0 x 10.00 = 0). This seemingly simple property is fundamental to many mathematical concepts and calculations.
Error Handling and Accuracy
While 10.00 x 20 seems simple, it's crucial to understand error handling and accuracy in practical applications. Human error can occur during manual calculations, leading to mistakes. Using calculators or spreadsheets minimizes these errors but doesn't eliminate them entirely. Understanding significant figures and rounding is essential for maintaining accuracy in calculations.
Advanced Concepts: Matrices and Linear Algebra
While beyond the scope of a basic multiplication problem, it's worth noting that the concept of multiplication extends to more advanced mathematical structures like matrices. Matrix multiplication is a fundamental operation in linear algebra, with wide-ranging applications in computer graphics, physics, and engineering.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 10 x 20 and 10.00 x 20?
A: Mathematically, there's no difference in the result; both equal 200. However, 10.00 indicates greater precision, suggesting that the value is exactly 10 and not an approximation. This difference is significant in contexts where high accuracy is crucial, such as scientific measurements or financial calculations.
-
Q: How can I quickly calculate 10.00 x 20 in my head?
A: The simplest method is to recognize that multiplying by 10 involves moving the decimal point one place to the right. Therefore, 10.00 x 20 is equivalent to 10.00 x (10 x 2) = (10.00 x 10) x 2 = 100 x 2 = 200.
-
Q: Are there any tricks to make multiplying larger numbers easier?
A: Yes, several techniques exist, including using the distributive property, breaking down numbers into smaller components, and leveraging mental math strategies. Practice and familiarity with these methods improve speed and accuracy.
-
Q: What if I need to multiply 10.00 by a number that isn't a whole number?
A: Multiplying by decimals or fractions follows similar rules. Remember the place value of the digits after the decimal point and use standard multiplication methods, carefully accounting for decimal points.
-
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental building block of mathematics and is essential for problem-solving in various fields. A solid understanding of multiplication enables better comprehension of more advanced mathematical concepts and has practical applications in daily life and various professions.
Conclusion: The Enduring Power of a Simple Equation
The equation 10.00 x 20 might seem deceptively simple at first glance. However, a deeper exploration reveals the rich underlying principles of multiplication, its extensive practical applications, and its connection to more complex mathematical ideas. From basic arithmetic to advanced concepts in linear algebra, the foundations laid by this simple equation extend far beyond its immediate answer of 200. Mastering multiplication isn't just about getting the right number; it's about developing a deeper understanding of numerical relationships and their widespread influence across numerous aspects of our world. This understanding is critical for success in various academic and professional pursuits.
Latest Posts
Latest Posts
-
750ml En Oz
Sep 14, 2025
-
20 Of 21
Sep 14, 2025
-
Calcium Carbonate Hydrochloric
Sep 14, 2025
-
Factorise 6x 4
Sep 14, 2025
-
181cm In Inches
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10.00 X 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.