1/6 Of 120
stanleys
Sep 24, 2025 · 5 min read
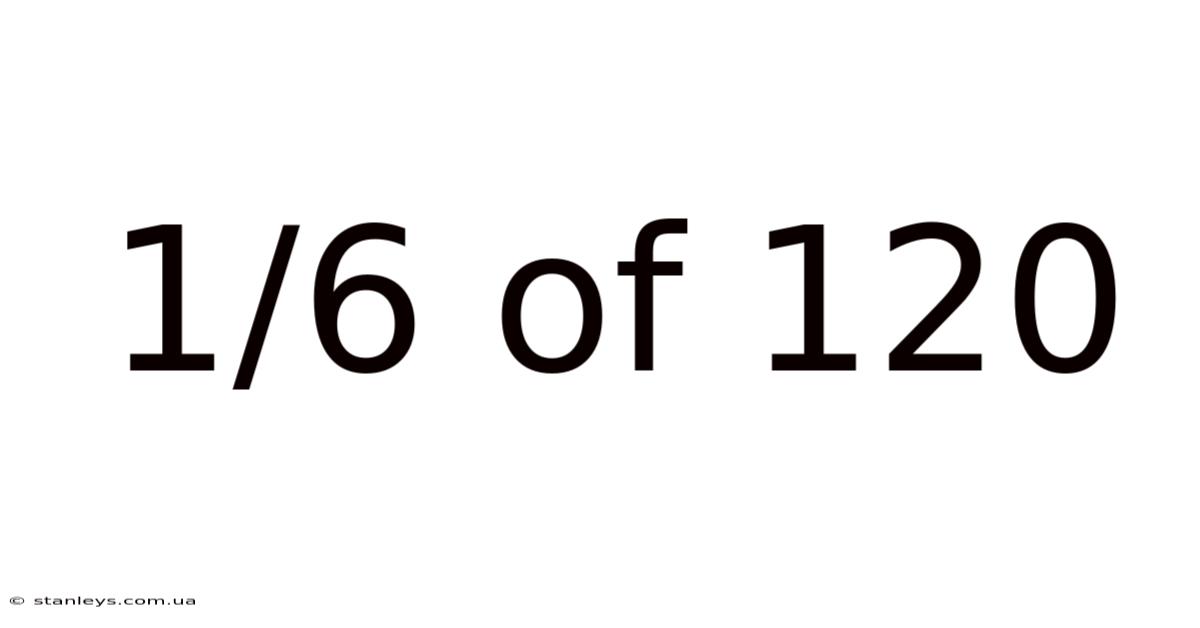
Table of Contents
Unlocking the Power of Fractions: A Deep Dive into 1/6 of 120
Finding a fraction of a number might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to a world of mathematical problem-solving. This article will explore the calculation of 1/6 of 120, providing a step-by-step guide, explaining the underlying principles, and delving into related concepts to build a solid foundation in fractions. We’ll also examine real-world applications and address frequently asked questions to ensure a complete understanding of this fundamental mathematical operation.
Understanding Fractions: A Quick Refresher
Before we dive into calculating 1/6 of 120, let's briefly review the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/6, 1 is the numerator and 6 is the denominator. This means we're dealing with one part out of six equal parts.
Calculating 1/6 of 120: A Step-by-Step Guide
There are two primary methods to calculate 1/6 of 120:
Method 1: Multiplication
This is the most straightforward method. To find a fraction of a number, we multiply the fraction by the number. In this case:
1/6 * 120 = ?
To perform this multiplication, we can convert the whole number (120) into a fraction by putting it over 1:
(1/6) * (120/1) = ?
Now, we multiply the numerators together and the denominators together:
(1 * 120) / (6 * 1) = 120/6
Finally, we simplify the fraction by dividing the numerator by the denominator:
120 ÷ 6 = 20
Therefore, 1/6 of 120 is 20.
Method 2: Division
Alternatively, we can approach this problem using division. Since we're finding 1/6 of 120, we can first divide 120 into six equal parts and then take one of those parts.
120 ÷ 6 = 20
This directly gives us the answer: 20. This method highlights the intuitive understanding of fractions – dividing the whole into equal parts.
Visualizing the Calculation
Imagine you have 120 apples. To find 1/6 of these apples, you would divide the 120 apples into six equal groups. Each group would contain:
120 apples / 6 groups = 20 apples/group
Therefore, one-sixth (1/6) of the apples is 20 apples. This visual representation reinforces the concept and makes it easier to grasp.
Expanding the Concept: Finding Other Fractions of 120
Understanding the calculation of 1/6 of 120 allows us to easily find other fractions of the same number. For example:
- 2/6 of 120: Since 1/6 of 120 is 20, 2/6 of 120 would be 2 * 20 = 40. Notice that 2/6 simplifies to 1/3, meaning 1/3 of 120 is also 40.
- 3/6 of 120: This is equivalent to 1/2 of 120, which is 120 / 2 = 60.
- 4/6 of 120: This simplifies to 2/3 of 120, which is 2 * 20 = 80, or 120 * 2/3 = 80
- 5/6 of 120: This would be 5 * 20 = 100.
- 6/6 of 120: This represents the entire amount, which is 120.
Real-World Applications
The ability to calculate fractions is vital in many everyday situations:
- Cooking and Baking: Recipes often call for fractions of ingredients (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
- Shopping: Understanding discounts and sales often involves calculating fractions (e.g., 20% off is equivalent to 1/5 off).
- Construction and Engineering: Accurate measurements and calculations are essential, frequently involving fractions and proportions.
- Finance and Budgeting: Managing personal finances requires understanding fractions and percentages.
- Data Analysis: Data representation and interpretation often involve working with fractions and proportions.
Further Exploration: Working with More Complex Fractions
While 1/6 of 120 is a relatively simple calculation, the principles can be extended to more complex scenarios involving larger numbers and more complicated fractions:
- Improper Fractions: Fractions where the numerator is larger than the denominator (e.g., 7/6) represent values greater than one.
- Mixed Numbers: These combine a whole number and a fraction (e.g., 1 1/2). To work with mixed numbers, convert them into improper fractions first.
- Decimals: Fractions can be expressed as decimals. For example, 1/6 is approximately 0.1667.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate a fraction of a number?
A: The easiest way is usually multiplication. Multiply the fraction by the number. Remember to convert the whole number into a fraction by placing it over 1.
Q: What if the fraction and number don't easily simplify?
A: Even if the fraction and number don't simplify directly, you can still multiply the numerators and denominators and then simplify the resulting fraction.
Q: Are there any online tools or calculators that can help?
A: Yes, many online calculators can help you calculate fractions of numbers. These tools can be especially useful for more complex calculations.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various examples, use visual aids, and try to apply fraction concepts to real-world problems.
Conclusion: Mastering Fractions – A Building Block for Mathematical Success
Understanding how to calculate fractions, such as finding 1/6 of 120, is a fundamental skill in mathematics. This seemingly simple calculation forms the bedrock for understanding more complex mathematical concepts. By mastering fractions, you unlock a deeper understanding of proportions, ratios, percentages, and many other essential mathematical tools crucial for success in various academic and professional fields. Through consistent practice and application, you'll build confidence and proficiency in working with fractions, making them an invaluable asset in your mathematical toolkit. Remember, every mathematical journey starts with small steps – and understanding the basics of fractions is an important first step towards greater mathematical fluency.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1/6 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.