1.5 X 7
stanleys
Sep 21, 2025 · 6 min read
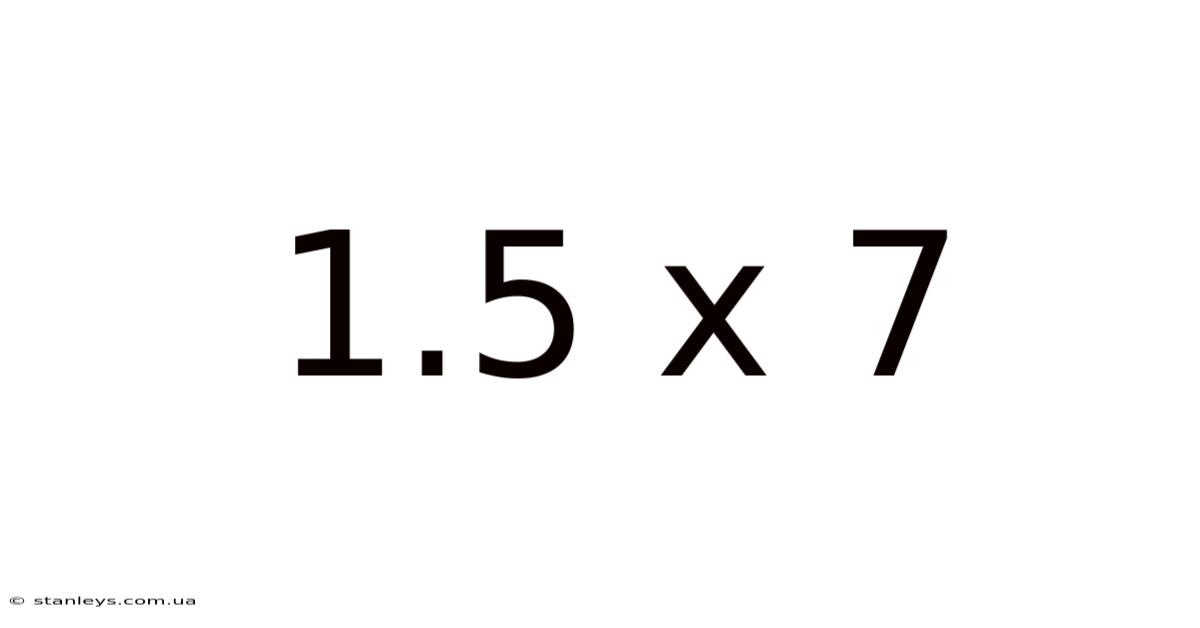
Table of Contents
Decoding 1.5 x 7: Exploring the Dimensions and Applications of this Common Ratio
The seemingly simple expression "1.5 x 7" represents far more than a basic multiplication problem. Understanding its implications delves into various fields, from simple geometry and scaling to more complex scenarios involving ratios, proportions, and even financial calculations. This article will explore the multifaceted nature of 1.5 x 7, examining its mathematical foundations, practical applications, and broader implications. We'll unravel the meaning behind this ratio, uncover its hidden uses, and show how this seemingly simple calculation can be a powerful tool for understanding the world around us.
Understanding the Basics: 1.5 x 7 = 10.5
The fundamental calculation is straightforward: 1.5 multiplied by 7 equals 10.5. This is a foundational concept in arithmetic, forming the basis for more complex mathematical operations. However, the significance extends beyond the simple answer. The numbers themselves, 1.5 and 7, represent values that frequently appear in practical applications across diverse fields. 1.5, or 3/2, signifies a 50% increase or a ratio of 3:2. The number 7 is a prime number, often appearing in natural patterns and having unique properties in mathematics.
Practical Applications Across Diverse Fields
The ratio 1.5 x 7, resulting in 10.5, finds practical use in numerous scenarios:
1. Scaling and Dimensioning:
-
Construction and Engineering: Imagine designing a rectangular structure. If one side measures 7 units (meters, feet, etc.), and the other side needs to be 1.5 times larger, the calculation 1.5 x 7 yields the required dimension of 10.5 units. This is fundamental in blueprint creation and architectural design. Understanding this ratio allows for accurate scaling and proportional representation of structures.
-
Graphic Design and Image Manipulation: In image editing software, resizing an image often involves adjusting dimensions proportionally. If you want to increase the width of an image by 50% (represented by 1.5), and the original width is 7 units (pixels, inches, etc.), the new width will be 10.5 units. Maintaining the aspect ratio is crucial for preserving image quality.
-
Manufacturing and Production: Many manufacturing processes involve scaling components or materials. If a specific part requires a length of 7 units, and a larger version needs to be 1.5 times the size, the calculation directly provides the necessary length of 10.5 units. This precision is vital for ensuring proper fitting and functionality.
2. Ratio and Proportion Problems:
-
Recipe Scaling: Cooking often involves adjusting recipes to serve more or fewer people. If a recipe calls for 7 units of an ingredient and you want 1.5 times the amount, the calculation provides the necessary quantity (10.5 units). This is crucial for consistent results when scaling recipes up or down.
-
Financial Calculations: The ratio can be applied in financial scenarios. For example, if an investment grows by 50% (1.5) over a period, and the initial investment was equivalent to 7 units (dollars, euros, etc.), the final value would be 10.5 units. This simplified example demonstrates how ratios can be used in more complex financial models.
-
Scientific Measurements: In scientific experiments, scaling quantities is common. If an experiment requires 7 milliliters of a solution, and a larger-scale experiment needs 1.5 times the amount, the calculation accurately determines the required volume of 10.5 milliliters.
3. Geometric Applications:
-
Area Calculations: While less direct, the numbers can be incorporated into area calculations. A rectangle with sides of 7 and 10.5 units would have an area of 73.5 square units. Understanding the ratio helps in quickly determining the area given one side.
-
Volume Calculations: Similarly, in three-dimensional objects, if one dimension is 7 units and another is 1.5 times that, the calculation provides a dimension crucial for determining volume. The specific application depends on the shape of the object.
Deeper Dive: Mathematical Implications
Beyond its practical applications, the expression 1.5 x 7 highlights important mathematical concepts:
-
Decimal Multiplication: The calculation involves multiplying a decimal number (1.5) by a whole number (7). Mastering this skill is crucial for handling various mathematical and real-world problems involving decimal values.
-
Fractional Equivalents: 1.5 is equivalent to the fraction 3/2. Understanding fractional equivalents allows for the use of different representations of the same numerical value, enhancing flexibility in calculations. The problem could be solved as (3/2) x 7 = 21/2 = 10.5.
-
Ratio and Proportion: The expression inherently represents a ratio of 1.5 to 1, or a proportion where one quantity is 1.5 times another. This concept is fundamental in algebra and various mathematical fields.
-
Linear Relationships: The relationship between the two numbers is linear; a direct proportional relationship exists, where a change in one variable directly affects the other. This forms the basis of many mathematical models and graphs.
Addressing Potential Misconceptions
While the calculation itself is straightforward, some misconceptions might arise:
-
Units of Measurement: It's crucial to remember that the "units" involved depend entirely on the context. The answer 10.5 represents 10.5 of whatever unit was used initially (meters, inches, pixels, etc.). Always pay attention to the units in practical applications.
-
Rounding: Depending on the application, rounding the answer (10.5) might be necessary. In some cases, rounding to 10 or 11 might be appropriate, depending on the level of precision required. However, for most applications, the precise value of 10.5 is crucial.
-
Contextual Understanding: The significance of the ratio depends entirely on the context in which it is used. Understanding the specific application is vital to interpreting the results accurately.
Frequently Asked Questions (FAQ)
Q: Can 1.5 x 7 be applied to more complex calculations?
A: Absolutely. This simple multiplication forms the building block for many more complex calculations involving ratios, proportions, and algebraic expressions. Understanding this fundamental calculation is essential for mastering more advanced mathematical concepts.
Q: What are some alternative ways to solve 1.5 x 7?
A: Besides direct multiplication, you can convert 1.5 to the fraction 3/2 and perform fractional multiplication: (3/2) x 7 = 21/2 = 10.5. You could also use distributive property: 1 x 7 + 0.5 x 7 = 7 + 3.5 = 10.5
Q: Are there any real-world examples where the result 10.5 is significant?
A: The significance of 10.5 depends on the context. In a construction project, it could represent 10.5 meters of a wall. In a recipe, it might mean 10.5 ounces of an ingredient. The importance lies in the application, not the numerical value itself.
Q: How does understanding 1.5 x 7 improve mathematical skills?
A: Mastering this simple calculation reinforces understanding of decimal multiplication, fractional equivalents, ratios, and proportions – all fundamental building blocks of more advanced mathematical concepts.
Conclusion: The Ubiquitous Nature of 1.5 x 7
The seemingly simple calculation of 1.5 x 7, resulting in 10.5, holds a significant role in various fields. From basic scaling and dimensioning in construction and design to more complex applications in finance and scientific measurements, understanding this ratio is crucial for tackling real-world problems. The concept extends beyond simple arithmetic, highlighting the importance of decimals, fractions, ratios, and proportions, forming a solid base for a deeper understanding of mathematics and its practical applications. Mastering this fundamental calculation empowers you to approach complex problems with increased confidence and analytical skills, reinforcing your overall mathematical proficiency. Its ubiquitous nature underscores the importance of even the seemingly simplest mathematical concepts in navigating the complexities of the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1.5 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.